目录
一、什么是频谱分辨率
1. 关于矩形窗函数
2. 分析余弦信号频谱
3. 频谱分辨率的定义
4. 如何提高频谱分辨率
二、关于频率估计
一、什么是频谱分辨率
1. 关于矩形窗函数
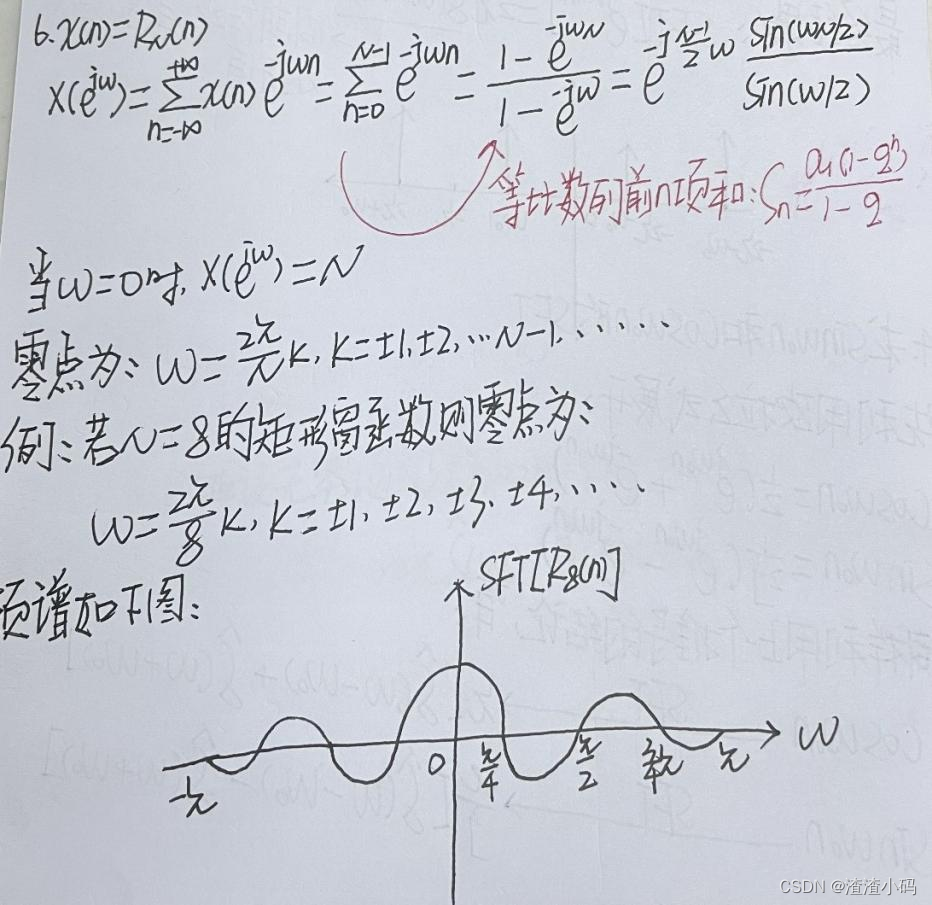 当k=1时,主瓣宽度就是2x
当k=1时,主瓣宽度就是2x,能量主要集中在主瓣部分,频谱泄露以及频谱分辨率等都与主瓣相关。
用 DFT 分析连续时间信号的频谱时,隐含对其采样后的序列利用矩形窗进行截断。比如余弦信号:频谱是两个冲激,时域上相乘,频域上就是频谱间的卷积运算(函数跟冲激做卷积,相当于是把函数直接移位到冲激上),那么就导致余弦信号的频谱在其数字角频率附近是具有一定宽度的主瓣,如下图,假设截取余弦信号的长度是M:

下面以分析一个余弦信号为例说明采样点数N(信号的采集时间)是如何影响频谱分析。
2. 分析余弦信号频谱
假设余弦信号中只有两个独立的频率分量,为f1和f1,序列长度N固定为100,FFT点数固定为1024,不断调整他们之间的距离,观察频谱。
(1) f1=10kHz,f2= 30kHz
samples=100;FFTN=1024;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=10;f2=30;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10(abs((fx(1:FFTN/2)))),'LineWidth',2);%k换算成对应的模拟频率
grid on;
xlabel('kHz','fontsize',12);
ylabel('|X(e^j\omega)|','fontsize',12);
axis([0 50 -10 35]);运行如下图:
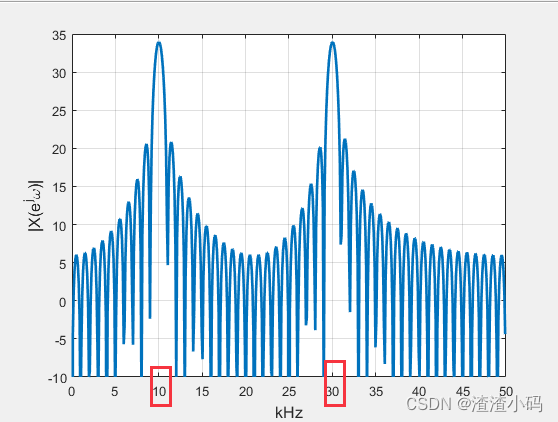
可以发现,这时候,两个主瓣相隔比较远,不会相互影响(旁瓣部分有重叠,但是旁瓣部分能量少,暂时不分析,可忽略)。
(2) 保持 f1 不变,减小 f2到11KHz,使其靠近 f1
samples=100;FFTN=1024;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=10;f2=11;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10(abs((fx(1:FFTN/2)))),'LineWidth',2);%k换算成对应的模拟频率
grid on;
xlabel('kHz','fontsize',12);
ylabel('|X(e^j\omega)|','fontsize',12);
axis([0 50 -10 35]);可以发现,这时候两个主瓣还是没有重叠的,频谱图上还是有两个尖峰(互不干涉),如下图:
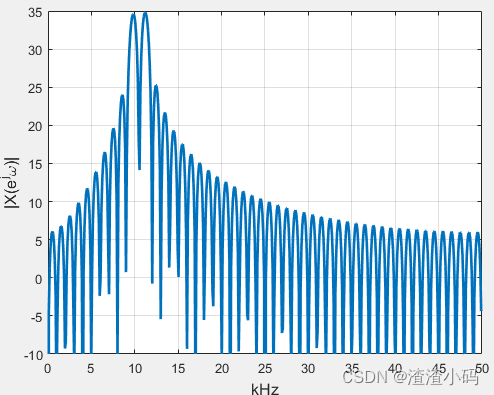
(3) 保持 f1 不变,减小 f2到10.8KHz,使其靠近 f1
samples=100;FFTN=1024;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=10;f2=10.8;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10(abs((fx(1:FFTN/2)))),'LineWidth',2);%k换算成对应的模拟频率
grid on;
xlabel('kHz','fontsize',12);
ylabel('|X(e^j\omega)|','fontsize',12);
axis([0 50 -10 35]);这时候,主瓣之间已经有部分重叠,如下图:
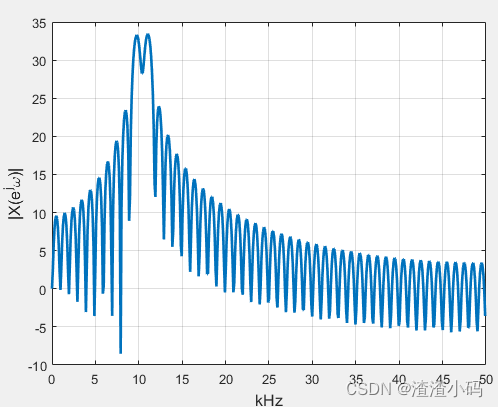
(4) 保持 f1 不变,减小 f2到10.5KHz,使其靠近 f1
samples=100;FFTN=1024;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=10;f2=10.5;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10(abs((fx(1:FFTN/2)))),'LineWidth',2);%k换算成对应的模拟频率
grid on;
xlabel('kHz','fontsize',12);
ylabel('|X(e^j\omega)|','fontsize',12);
axis([0 50 -10 35]);这时候已经没有两个独立的峰值了:

分析:
对单频正(余)弦信号而言,该主瓣的宽度B和序列的长度 N 满足以下关系式:
主瓣宽度是2x,即B=2x
,2pi对应的是Fs。其中 Fs 是采样频率。
当两个频率逐渐接近时,各自的主瓣对对方的影响增大。其中两个频率的间隔恰好是 B/2(比如f1 不变,减小 f2到11KHz),SFT 谱中有两个峰,这时候,主瓣是互不影响的;当两个频率的间隔小于 B/2,SFT 谱两个峰的区分逐渐模糊;直到最后,完全重合就只有一个峰了。
3. 频谱分辨率的定义
SFT 谱的频谱分辨率定义为F=,也就是矩形窗主瓣宽度的一半。当两个频率的间隔大于 B/2 时,SFT 谱中两个频率才是可区分的。
4. 如何提高频谱分辨率
采样率固定的情况下,加大采样时间(N增加),F减小,频谱分辨率可以提高。
示例:
(5) 保持 f1 不变,减小 f2到10.5KHz,使其靠近 f1。如果保持f1和f2的值,将序列的长度N增加到150。
samples=150;FFTN=1024;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=10;f2=10.5;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10(abs((fx(1:FFTN/2)))),'LineWidth',2);%k换算成对应的模拟频率
grid on;
xlabel('kHz','fontsize',12);
ylabel('|X(e^j\omega)|','fontsize',12);
axis([0 50 -10 40]);谱图中,又开始分辨出两个波峰:

二、关于频率估计
计算是存在误差的,并且不同的DFT点数结果也是不同的,在频谱图上,波峰的位置并不是严格对应到单频的频率分量,而是在其附近波动。
例:假设余弦信号中有f1=20.1KHz;f2=21.5KHz;信号采样点是90,做2048个点的FFT。
samples=90;FFTN=2048;%信号持续点数及 FFT 点数
n=0:samples-1;
Fs=100;%采样频率(kHz)
f1=20.1;f2=21.5;%信号频率(kHz)
x=cos(2*pi*f1/Fs*n)+2*cos(2*pi*f2/Fs*n);
fx=fft(x,FFTN);%设定 FFT 点数为 FFTN
df=0.5;%频率搜索范围-df->df
dk=floor(df/Fs*FFTN);%与之对应的 k
k1=floor(f1/Fs*FFTN);
k2=floor(f2/Fs*FFTN);
[m,k]=max(abs(fx(k1-dk:k1+dk))); [k+k1-dk-2 (k+k1-dk-2)/FFTN*Fs]
[m,k]=max(abs(fx(k2-dk:k2+dk))); [k+k2-dk-2 (k+k2-dk-2)/FFTN*Fs]
figure;
plot((0:FFTN/2-1)/FFTN*Fs,20*log10((abs((fx(1:FFTN/2))))),'b','LineWidth',2);grid on;
xlabel('kHz','fontsize',12);ylabel('|X(e^j\omega)|','fontsize',12);axis([0 50 -10 40]);频谱图如下:
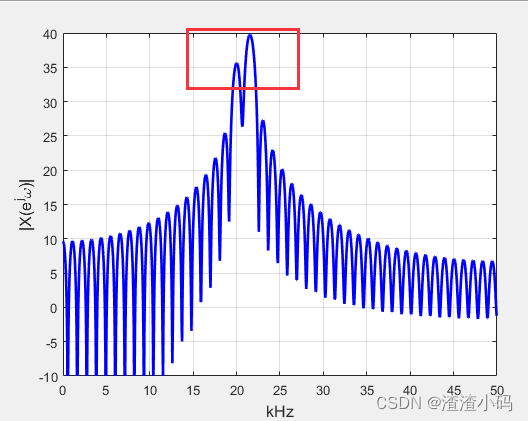
局部搜索极值,求出其对应的k,并不是严格等于原来的k值,用求出的k再去计算对应的模拟频率,和原模拟频率是有偏差的。
结果如下:













)



【sort/cmp的灵活应用】)


