数据结构——树与二叉树

目录

树与二叉树

1.树的定义

2.树的有关术语

3.二叉树（BinaryTree）

二叉树的性质：

特殊的二叉树

·满二叉树：

·完全二叉树

二叉树的存储结构 

顺序存储结构

链式存储结构

二叉树以及对应接口的实现

1.二叉树架构搭建

2.二叉树的创建

3.二叉树的销毁

4.二叉树的前中后序

5.求树的节点个数

6.求叶子结点个数(无左右孩子，度为0)

7.求树的深度

8.二叉树的层序遍历

顾名思义就是一层一层从左到右遍历

 拓展知识

树与二叉树

1.树的定义

树是n（n>=0）个结点构成的有限集合。

·当n=0时，称为空树

·树中有一个特殊的结点被称作“根（root）”，其余结点可以分为m个不相交的有限集，其中每一个   集合都是一颗树，被称为原来树的子树。（对于空树来说）

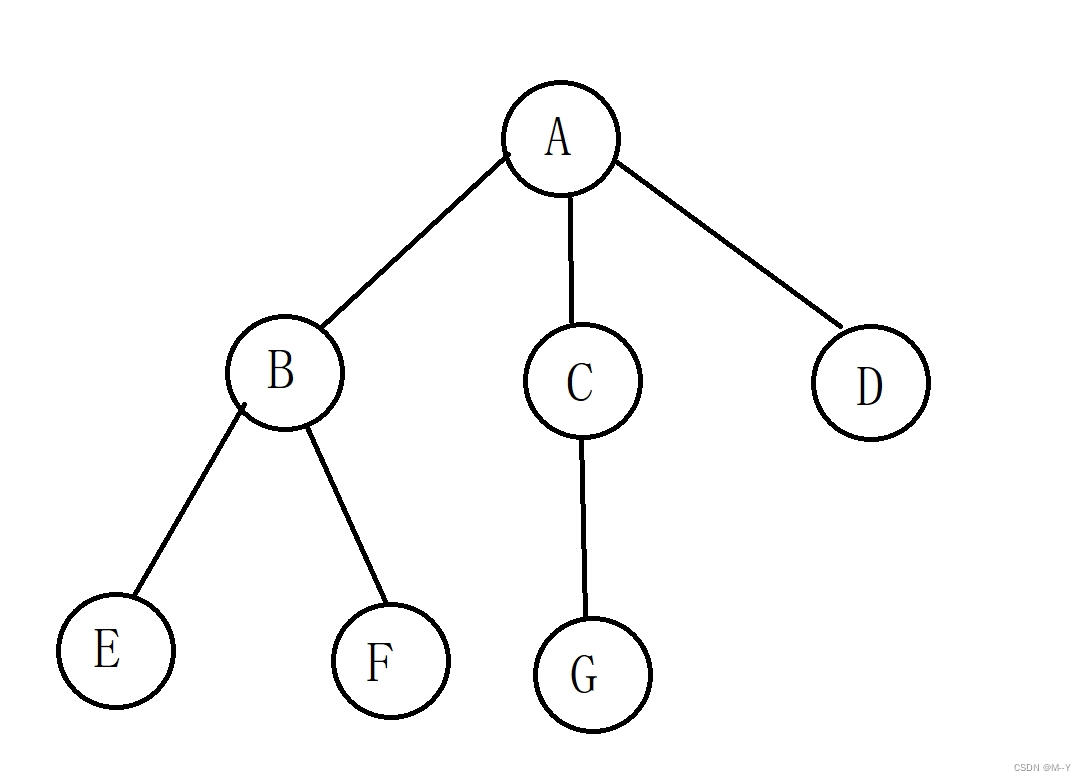
2.树的有关术语

（1）结点：树中独立的单元格，包含一个数据元素及若干指向子树的分支。

（2）结点的度：结点的子树个数

（3）树的度：树中最大的结点的度，上图树的度为3.

（4）叶子结点：树中度为0的节点，叶子是这一类结点的总称。上图中的E、F、G、D都是叶子节点。

（5）双亲结点：有子树的结点，是其子树的双亲结点。上图的A就是B、C、D的双亲结点

（6）子结点：上图B、C、D是A的子结点

（7）兄弟结点：上图B、C、D互为兄弟结点

（8）结点的层次：根结点在1层，其他结点的层次等于其父节点的层次+1

  (9)   树的深度：所有结点中最大的层次就是树的深度

（10）森林：m棵不相交的树的集合

3.二叉树（BinaryTree）

二叉树是特殊的树，该树每个结点的度<=2。

二叉树的性质：

1.二叉树在第k层上最多有2^(k-1）个结点

2.深度为k的二叉树最多有2^k-1个结点

3.一颗二叉树如果度为0的结点有N0个，度为2的结点有N2个，则N0=N2+1

特殊的二叉树

·满二叉树：

深度为k且一共有2^k-1个结点，第i层的节点树为2^(i-1)

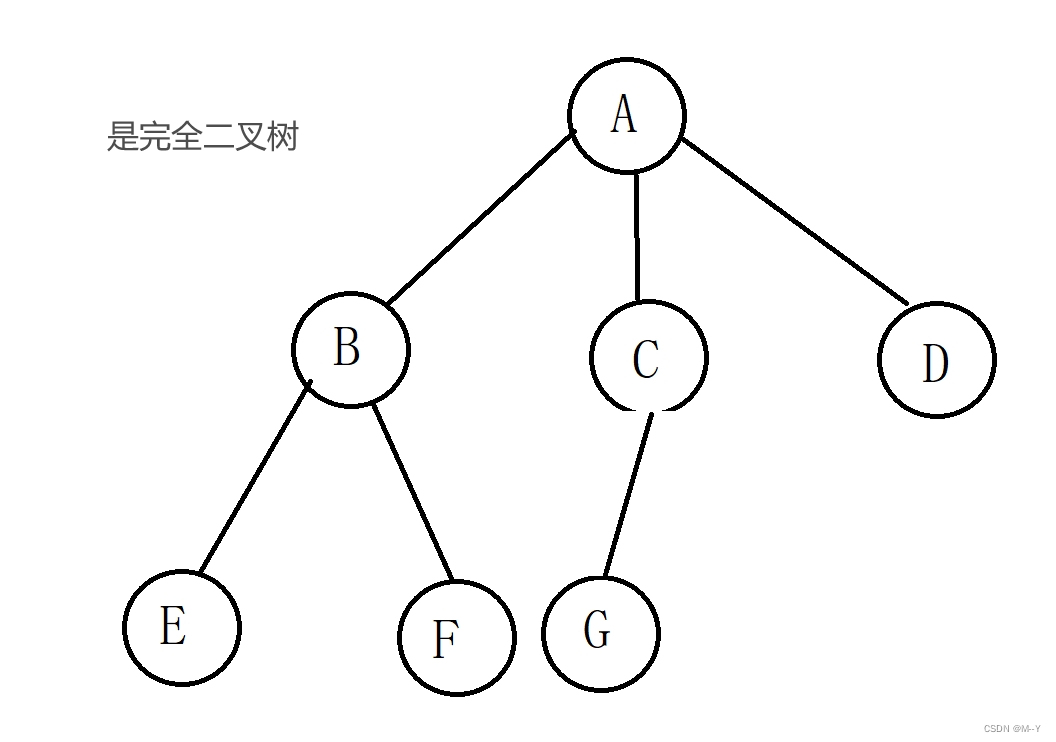
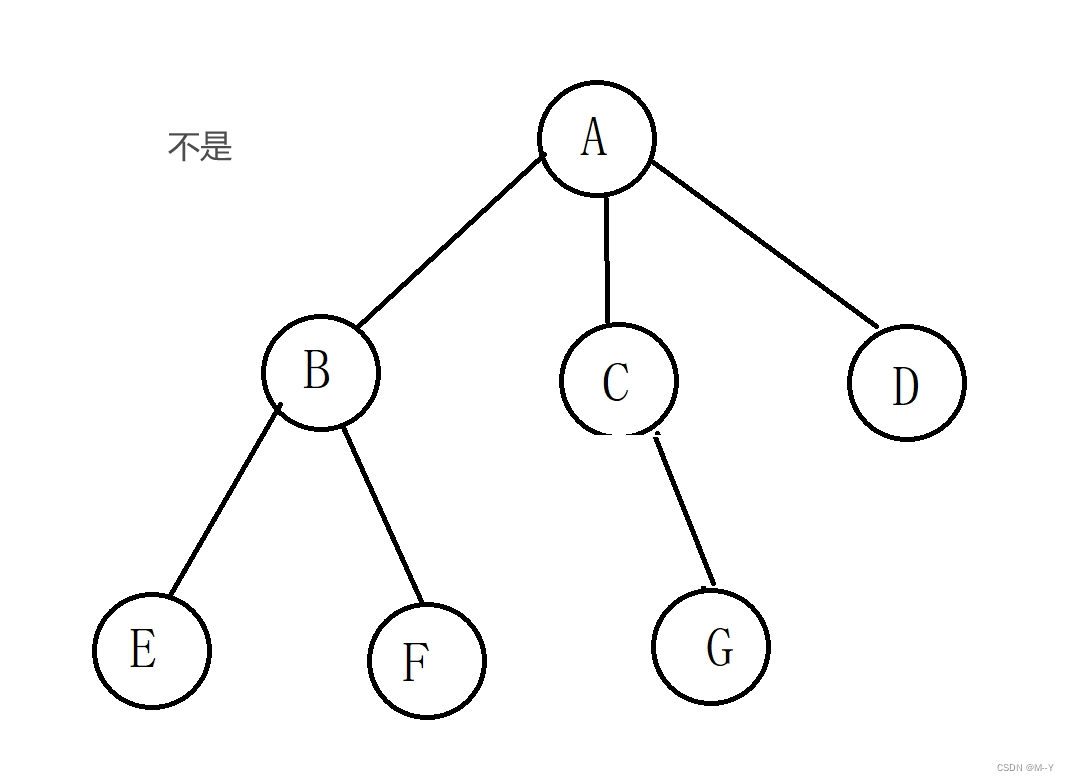
·完全二叉树

深度为k，前k-1层每层都是满结点，最后退成结点从左向右连续排列

二叉树的存储结构 

顺序存储结构

用数组存储二叉树，按从上到下，从左到右顺序存储。（比较适合满二叉树和完全二叉树）

对于普通的二叉树，存储起来空元素的结点就会导致空间的浪费

链式存储结构

这里最常用的存储类型就是运用两指针

1.两指针分别是左右孩子

2.两指针分别是左孩子和右兄弟

二叉树以及对应接口的实现

1.二叉树架构搭建

typedef char BTDataType;//利于适用于多种类型的数据操作

typedef  struct BinaryTree

{

        BTDataType val;

        struct BinaryTree*left;

        struct BinaryTree*right;//左右孩子指针

}BTNode;

2.二叉树的创建

BTNode* BTbyNode(BTDataType x)

{

        BTNode*newnode=(BTNode*)malloc(sizeof(BTNode));

        if(newnode==NULL)

        {

                perror("malloc fail!!!");

                return NULL;

        }

        newnode->val=x;

        newnode->left=NULL;

        newnode->right=NULL;

        

        return newnode;

}

BTNode* CreateTree()
{
    BTNode* l1 = BTByNode(1);
    BTNode* l2 = BTByNode(2);
    BTNode* l3 = BTByNode(3);
    BTNode* l4 = BTByNode(4);
    BTNode* l5 = BTByNode(5);

    l1->left = l4;
    l1->right = l2;
    l2->left = l3;
    l4->right = l5;

    return l1;
}

3.二叉树的销毁

void TreeDestroy(BTNode*root)

{

        if(root==NULL)

                return ;

        TreeDestroy(root->left);

        TreeDestroy(root->right);

        free(root);

        //root==NULL//这里是局部变量，在函数内部置空没有用，要在调用销毁函数的下面置空root

} 

4.二叉树的前中后序

关于二叉树非常重要的一个思想就是分治思想，将大问题转化成多个小问题去解决。换成二叉树也就是，将根节点问题不断转化给左右子树

void PrevOrder(BTNode*root)//前序----根---左---右

{

        if(root==NULL)

                return ；

        printf("%c  ",root->val);

        PrevOrder(root->left);

        PrevOrder(root->right);

} 

 void InOrder(BTNode*root)//中序----左---根---右

{

        if(root==NULL)

                return ;

        InOrder(root->left);

        printf("%c  ",root->val);

        InOrder(root->right);

}

void PostOrder(BTNode*root)//后序----左---右---根

{

        if(root==NULL)

                return ;

        PostOrder(root->left);

        PostOrder(root->right);

        printf("%c  ",root->val);

} 

5.求树的节点个数

int BinaryTreeSize(BTNode* root)

{

        return root==NULL?0:BinaryTreeSize(root->left)

                                        +BinaryTreeSize(root->right)+1;

} 

6.求叶子结点个数(无左右孩子，度为0)

int BinaryTreeleafSize(BTNode* root)

{

        if(root==NULL)

                return 0;

        if(root->left==NULL&&root->right==NULL)

                return 1；

        return BinaryTreeleafSize（root->left）+BinaryTreeleafSize(root->right);

} 

7.求树的深度

int BinaryTreeHeight(BTNode* root)

{

        if(root==NULL)

                return 0;

        int h1=BinaryTreeHeight(root->left);

        int h2=BinaryTreeHeight(root->right);

        return h1>h2?h1:h2;

} 

8.二叉树的层序遍历

顾名思义就是一层一层从左到右遍历

用一个队列来实现当一个根节点出队列，就将它的左右结点入队列，直到队列中无元素

void TreeLevelOrder(BTNode* root)

{

        Queue q;//创建一个队列对象

        QueueInit(&q);//队列初始化

        if(root)

                QueuePush(&q,root);//将根结点指针入队列

        

        while(!QueueEmpty(&q))//判断队列是否为空，为空说明遍历结束

        {

                BTNode*front=QueueFront(&q);//取队首元素,防止下面出队首元素找不到根结点位置

                QueuePop(&q);//将队首元素出队列

                if(front)

                {

                        printf("%c ",front->val);

                        QueuePush(&q,front->left);

                        QueuePush(&q,front->right);//将左右孩子入队列

                 }

        }

        TreeDestroy(root);

        root==NULL;

} 

 拓展知识

知道一个树的结点数量，怎么算出该树的可能有几种情况

我们定义f(n)表示结点数为n的二叉树的情况数

零个结点也是一种情况，所以f(0)=1;

一个结点时，只有一种情况，则f(1)=1;

两个结点时，有两种情况，根结点一个，剩下结点左右孩子各一种情况，则f(2)=f(1)+f(1)=2;

三个结点时，根节点一个节点，剩下结点分为三种情形：

1.左子树两个结点右子树零个

2.右子树两个结点左子树零个

3.左右子树各一个节点

则f(3)=f(2)*f(0)+f(1)*f(1)+f(0)*f(2)

经过推算得到f(n)=f(n-1)*f(0)+f(n-2)*f(1)+…+f(0)*f(n-1)

上述式子可以化简成（2n)! / ( n! (n+1)! )在数学中被称为卡特兰数

有了上述式子知道结点数就能轻松算出树可能存在的情况数

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/766826.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

关于 Microsoft Visual Studio

关于 Microsoft Visual Studio

关于 Microsoft Visual Studio References References [1] Yongqiang Cheng, https://yongqiang.blog.csdn.net/
阅读更多...
【机器学习300问】47、如何计算AUC？

【机器学习300问】47、如何计算AUC？

一、AUC是什么&#xff1f; &#xff08;1&#xff09;文绉绉的定义 AUCArea Under the Curve中文直译叫“曲线下面积”&#xff0c;AUC名字里面的Curve曲线指的就是ROC曲线&#xff0c;关于ROC曲线的相关知识我已经在之前的文章中详细说过了&#xff0c;有需要的友友可以点击…
阅读更多...
CI/CI实战-jenkis结合gitlab 4

CI/CI实战-jenkis结合gitlab 4

实时触发 安装gitlab插件 配置项目触发器 生成令牌并保存 配置gitlab 测试推送 gitlab的实时触发 添加jenkins节点 在jenkins节点上安装docker-ce 新建节点server3 安装git和jdx 在jenkins配置管理中添加节点并配置从节点 关闭master节点的构建任务数
阅读更多...
革新水库大坝监测：传统软件与云平台之比较

革新水库大坝监测：传统软件与云平台之比较

在水库大坝的监测管理领域&#xff0c;传统监测软件虽然曾发挥了重要作用&#xff0c;但在多方面显示出了其局限性。传统解决方案通常伴随着高昂的运维成本&#xff0c;需要大量的硬件支持和人员维护&#xff0c;且软件整合和升级困难&#xff0c;限制了其灵活性和扩展性。 点击…
阅读更多...
Neo4j桌面版导入CVS文件

Neo4j桌面版导入CVS文件

之后会出来一个提示框&#xff0c;而且会跳出相关文件夹&#xff1a; 然后我们将CSV文件放在此目录下&#xff1a; 我们的relation.csv是这样的 参见&#xff1a; NEO4J的基本使用以及桌面版NEO4J Desktop导入CSV文件_neo4j desktop使用-CSDN博客
阅读更多...
C++11：左值与右值|移动构造|移动赋值

C++11：左值与右值|移动构造|移动赋值

​ &#x1f3ac;慕斯主页&#xff1a;修仙—别有洞天 ♈️今日夜电波&#xff1a;マイノリティ脈絡—ずっと真夜中でいいのに。 0:24━━━━━━️&#x1f49f;──────── 4:02 &#x1f504; …
阅读更多...
MySQL表内容的增删查改

MySQL表内容的增删查改

在前面几章的内容中我们学习了数据库的增删查改&#xff0c;表的增删查改&#xff0c;这一篇我们来学习一下对表中的内容做增删查改。 CRUD : Create(创建), Retrieve(读取)&#xff0c;Update(更新)&#xff0c;Delete&#xff08;删除&#xff09; 1.创建Create 我们先创建…
阅读更多...
Zabbix Web界面中文汉化

Zabbix Web界面中文汉化

要想达到上图的效果&#xff0c;第一步先查看 /usr/share/zabbix/assets/fonts/ [rootservice yum.repos.d]# ll /usr/share/zabbix/assets/fonts/ 总用量 0 lrwxrwxrwx. 1 root root 33 3月 23 16:58 graphfont.ttf -> /etc/alternatives/zabbix-web-font 继续查看graph…
阅读更多...
基于霍夫检测（hough变换）的人眼瞳孔定位，Matlab实现

基于霍夫检测（hough变换）的人眼瞳孔定位，Matlab实现

博主简介&#xff1a; 专注、专一于Matlab图像处理学习、交流&#xff0c;matlab图像代码代做/项目合作可以联系&#xff08;QQ:3249726188&#xff09; 个人主页&#xff1a;Matlab_ImagePro-CSDN博客 原则&#xff1a;代码均由本人编写完成&#xff0c;非中介&#xff0c;提供…
阅读更多...
vue实现饼图渲染的步骤

vue实现饼图渲染的步骤

1) 创建一个DOM对象,有自定义的高和宽. 2) 引入Echarts软件包并导入到对应文件内 npm i Echarts import 文件.js script src.../文件 3) 初始化一个对象 4) 对象的方法实现饼图渲染 data内的数据,且当一个对象已经渲染一遍,再执行这个,会对setOption的参数进行更新,其…
阅读更多...
Linux的学习之路：2、基础指令（1）

Linux的学习之路：2、基础指令（1）

一、ls指令 上篇文章已经说了一点点的ls指令&#xff0c;不过那还是不够的&#xff0c;这篇文章会介绍更多的指令&#xff0c;最起码能使用命令行进行一些简单的操作&#xff0c;下面开始介绍了 ls常用选项 -a 列出目录下的所有文件&#xff0c;包括以 . 开头的隐含文件。 -d…
阅读更多...
02课程发布模块之部署Nginx

02课程发布模块之部署Nginx

部署Nginx 部署网关 通过Nginx访问后台网关&#xff0c;然后由网关再将请求转发到具体的微服务,网关会把请求转发到具体的服务 upstream gatewayserver{server 127.0.0.1:63010 weight10; } # 网站首页对应的虚拟机 server {listen 80;server_name www.51xuecheng.cn…
阅读更多...
Yoast插件：您的WordPress网站SEO优化利器

Yoast插件：您的WordPress网站SEO优化利器

在之前的文章中我们介绍了如何低成本使用WordPress来搭建个人网站&#xff0c;相信很多朋友都希望自己的网站能够被搜索引擎所收录&#xff0c;并获得更高的排名&#xff0c;从而吸引更多的流量和用户。如果是的话&#xff0c;您需要了解SEO&#xff08;搜索引擎优化&#xff0…
阅读更多...
使用git+ssh访问github，避免下载资源失败

使用git+ssh访问github，避免下载资源失败

一、创建github账户之后&#xff0c;记住注册邮箱和账户名 我的邮箱&#xff1a;yuanyan23mails.ucas.ac.cn 账户名&#xff1a;thekingofjumpshoot 下边的相关位置需要用自己的邮箱和用户名替代 二、输入本地生成秘钥和公钥命令&#xff0c;并且生成公私钥对 ssh-keygen …
阅读更多...
初识进程的地址空间、页表

初识进程的地址空间、页表

一、&#x1f31f;问题引入 &#x1f6a9;代码一&#xff1a; #include<stdio.h>#include<unistd.h>int g_val100;int main(){pid_t idfork();if(id0){//子进程while(1){printf("I am a child pid:%d ppid:%d g_val:%d\n",getpid(),getppid(),g_val);…
阅读更多...
AOF 持久化是怎么实现的？

AOF 持久化是怎么实现的？

资料来源 : 小林coding 小林官方网站 : 小林coding (xiaolincoding.com) AOF 日志 试想一下&#xff0c;如果 Redis 每执行一条写操作命令&#xff0c;就把该命令以追加的方式写入到一个文件里&#xff0c;然后重启 Redis 的时候&#xff0c;先去读取这个文件里的命令&#xf…
阅读更多...
使用Intellij idea编写Spark应用程序(Scala+Maven)

使用Intellij idea编写Spark应用程序(Scala+Maven)

使用Intellij idea编写Spark应用程序(ScalaMaven) 对Scala代码进行打包编译时&#xff0c;可以采用Maven&#xff0c;也可以采用sbt&#xff0c;相对而言&#xff0c;业界更多使用sbt。这里介绍IntelliJ IDEA和Maven的组合使用方法。IntelliJ IDEA和SBT的组合使用方法&#xf…
阅读更多...
FANUC机器人零点标定的基本步骤（出厂数据）

FANUC机器人零点标定的基本步骤（出厂数据）

FANUC机器人零点标定的基本步骤（出厂数据） FANUC 零点数据存在问题的机器人通常会出现以下几种报警： （1）SRVO-062报警 - 脉冲编码器数据丢失，机器人完全不能动，具体消除方法可参考以下链接中的内容： FANUC机器人SRVO-062报警原因分析及处理对策 （2）SRVO-075报警 -…
阅读更多...
自己动手做一个批量doc转换为docx文件的小工具

自己动手做一个批量doc转换为docx文件的小工具

前言 最近遇到了一个需求&#xff0c;就是要把大量的doc格式文件转换为docx文件&#xff0c;因此就动手做了一个批量转换的小工具。 背景 doc文件是什么&#xff1f; “doc” 文件是一种常见的文件格式&#xff0c;通常用于存储文本文档。它是 Microsoft Word 文档的文件扩…
阅读更多...
探索 Flutter 中的 NavigationRail：使用详解

探索 Flutter 中的 NavigationRail：使用详解

1. 介绍 在 Flutter 中&#xff0c;NavigationRail 是一个垂直的导航栏组件&#xff0c;用于在应用程序中提供导航功能。它通常用于更大屏幕空间的设备&#xff0c;如平板电脑和桌面应用程序。NavigationRail 提供了一种直观的方式来浏览应用程序的不同部分&#xff0c;并允许…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023