•  503.下一个更大元素II 

与496.下一个更大元素 I的不同是要循环地搜索元素的下一个更大的数。那么主要是对于遍历结束后，单调栈里面剩下的那些元素。

如果直接把两个数组拼接在一起，然后使用单调栈求下一个最大值就可以。

代码实现的话，不用直接把数组后面再接一个数组，而是单调栈走2遍这个数组即可。

代码如下。第二次遍历使用取余的方法。
 

class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n=nums.size();vector<int> result(n,-1);stack<int> st;for(int i=0;i<2*n;++i){int k=i%n;while(!st.empty() && nums[k]>nums[st.top()]){result[st.top()]=nums[k];st.pop();}st.push(k);}return result;}
};

•  42. 接雨水  

依据列来计算更好理解，能引入单调栈：可以看出，因为左侧最高柱子和右侧最高柱子肯定不会存储雨水（左侧和右侧包含自己，因为自己是一侧最高的话不会存储雨水），所以每一列雨水的高度，取决于，该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。

下面图片以柱子4为例，可以看见中间所有柱子都满足这个结论，最两边的柱子不会存储雨水。

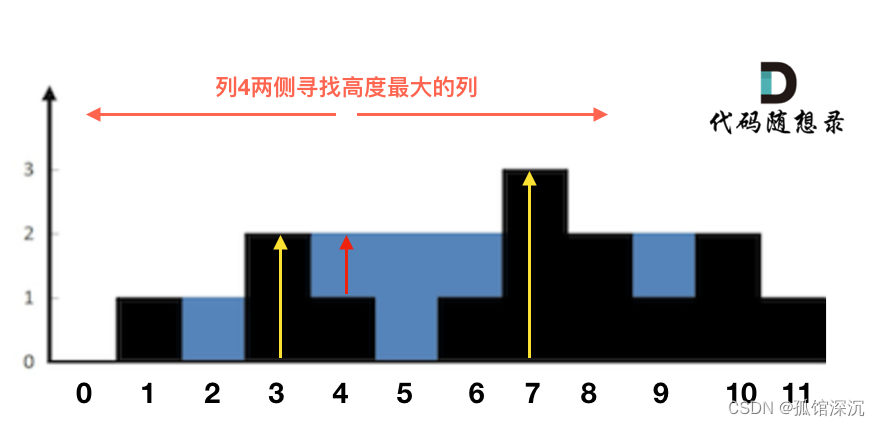
转化问题后，有3种办法解决：

• 会超时的暴力解法。
• 双指针优化。
• 重点的单调栈。

1、暴力解法。

对于每个元素，都从左、从右找最大高度的柱子lheight、rheight，所以外层循环是0到n-1，内层循环从i往左，然后从i往右找最大高度的柱子lheight、rheight，最多会查找n次。所以时间复杂度是O(n^2)，空间复杂度O(1)。但是会超时。

2、双指针优化。

当前元素的左边、右边最大高度的柱子lheight、rheight其实跟前一个元素的lheight、rheight有关。注意左边最大和右边最大要把自己考虑进去，如果不包含，左边最大/右边最大的可能比自己还小，那么相减是负数，最终结果比正确结果小。

当前i的lheight取决于左边i-1的lheight，rheight取决于右边i+1的rheight。具体如下：

当前i的lheight=max(前一个lheight，height[i])，所以需要从左到右得到lheight。

那么参照lheight，当前i的rheight应该=max(后一个lheight，height[i])，与上面相反，从右到左得到。

根据这个过程先把所有元素的lheight数组和rheight数组求出来，然后再遍历元素的时候，直接就是min(lheight[i],rheight[i])-height[i]。时间复杂度是O(n)，空间复杂度O(n)。

代码如下。

class Solution {
public:int trap(vector<int>& height) {int n=height.size();int l1,r1,l2,r2;int count=0;vector<int> lheight(n);vector<int> rheight(n);//初始化lheight[0]=height[0];rheight[n-1]=height[n-1];for(int i=1;i<n-1;++i){//中间元素的lheight和rheightlheight[i]=max(lheight[i-1],height[i]);rheight[i]=max(rheight[i+1],height[i]);}for(int i=n-2;i>0;--i){rheight[i]=max(rheight[i+1],height[i]);}for(int i=0;i<n;++i){if(i==0 || i==n-1)continue;int cur=min(lheight[i],rheight[i])-height[i];count+=cur;}return count;}
};

上面的1、2都是按照列的方式去装水，因为是找左右两边最大元素。

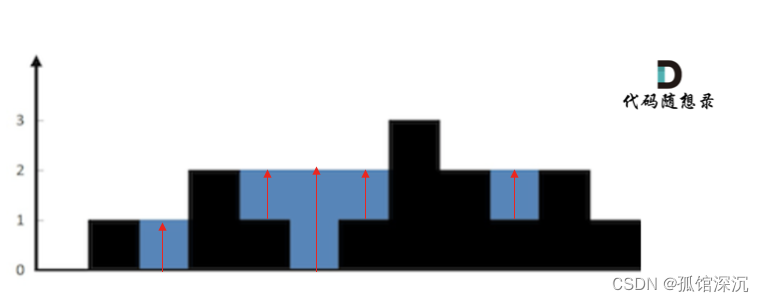
3、单调栈

如果按行装水的话，就可以通过下一个更大元素和上一个最大元素来求。

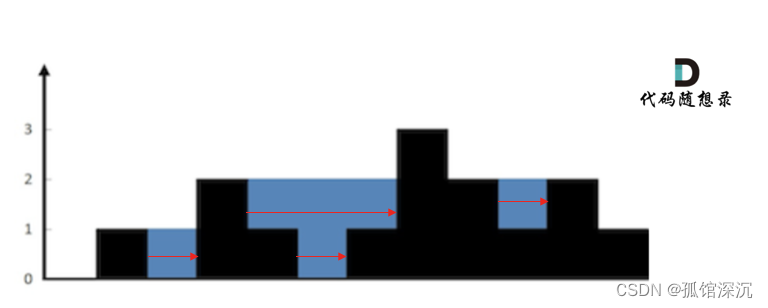
以上图为例，下标2左边更大是1，右边更大是2，所以自己这行（以下标2柱高0为底，以min(左边更大值，右边更大值)为高，宽度是2个更大值的距离1）可以存储1的雨水；下标4左边更大是2，右边更大是3，所以自己这行（以下标4柱高1为底，以min(左边更大值，右边更大值)=2为高，宽度是2个更大值的距离3）可以存储3的雨水……左边更大和右边更大有1个不存在的则存储雨水为0。

所以要用单调栈计算出上一个更大值和下一个更大值的下标leftmax和rightmax。然后i柱子处可以存储的雨水是：(min(height[leftmax],height[rightmax])-height[i])*(rightmax-leftmax-1)。

怎么计算上一个更大值和下一个更大值呢？还想着2次单调栈，实际上，1次单调栈即可。采用单调递增栈，在元素 i 比栈顶大的情况下，如果栈顶同时也比次栈顶要小，这个时候就出现一个凹槽，也就找到了上一个更大值（次栈顶）和下一个更大值（元素i）。所以这个单调递增栈，必须是严格的单增，这个凹槽一定是次栈顶>栈顶<比栈顶大的元素i。

所以如果元素i==栈顶的话，要么不操作，要么替换这个栈顶，才能满足单调栈。这里需要选择的操作是替换栈顶，因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

如果<栈顶，就直接入栈。

清晰说明了3种情况：

class Solution {
public:int trap(vector<int>& height) {int n=height.size();int count=0;stack<int> st;st.push(0);for(int i=1;i<n;++i){if(height[i]==height[st.top()]){st.pop();st.push(i);}else if(height[i]<height[st.top()])st.push(i);else{while(!st.empty()&&height[i]>height[st.top()]){//有凹槽,top是中间int mid=st.top();st.pop();if(!st.empty()){//取栈顶，都要判断非空int h=min(height[i],height[st.top()])-height[mid];//高int w=i-st.top()-1;//宽count+=w*h;}}st.push(i);}}return count;}
};

相等的情况pop()之前应该检查是否为空，但是初始和每一次循环结尾都有入栈操作，所以这里不用加。

简化。简化后的3个pop()操作都有可能遇栈空，所以都要加条件，否则报错：

class Solution {
public:int trap(vector<int>& height) {int n=height.size();int count=0;stack<int> st;st.push(0);for(int i=1;i<n;++i){while(!st.empty()&&height[i]>height[st.top()]){//有凹槽,top是中间int mid=st.top();st.pop();if(!st.empty()){//取栈顶，都要判断非空int h=min(height[i],height[st.top()])-height[mid];//高int w=i-st.top()-1;//宽count+=w*h;}}if(!st.empty()&&height[i]==height[st.top()]){st.pop();}st.push(i);}return count;}
};