491. 非递减子序列

本题并不能像 90.子集II 那样，使用排序进行树层去重。虽然题目没有明确不能排序，但如果排序了，集合本身就是递增子序列，这是LeetCode示例2中没有出现的。

所以本题的关键在于，如何在不排序的情况下对树层去重。在树层遍历的时候（也就是for循环），我们维护一个 used 数组，记录已经使用过的元素。

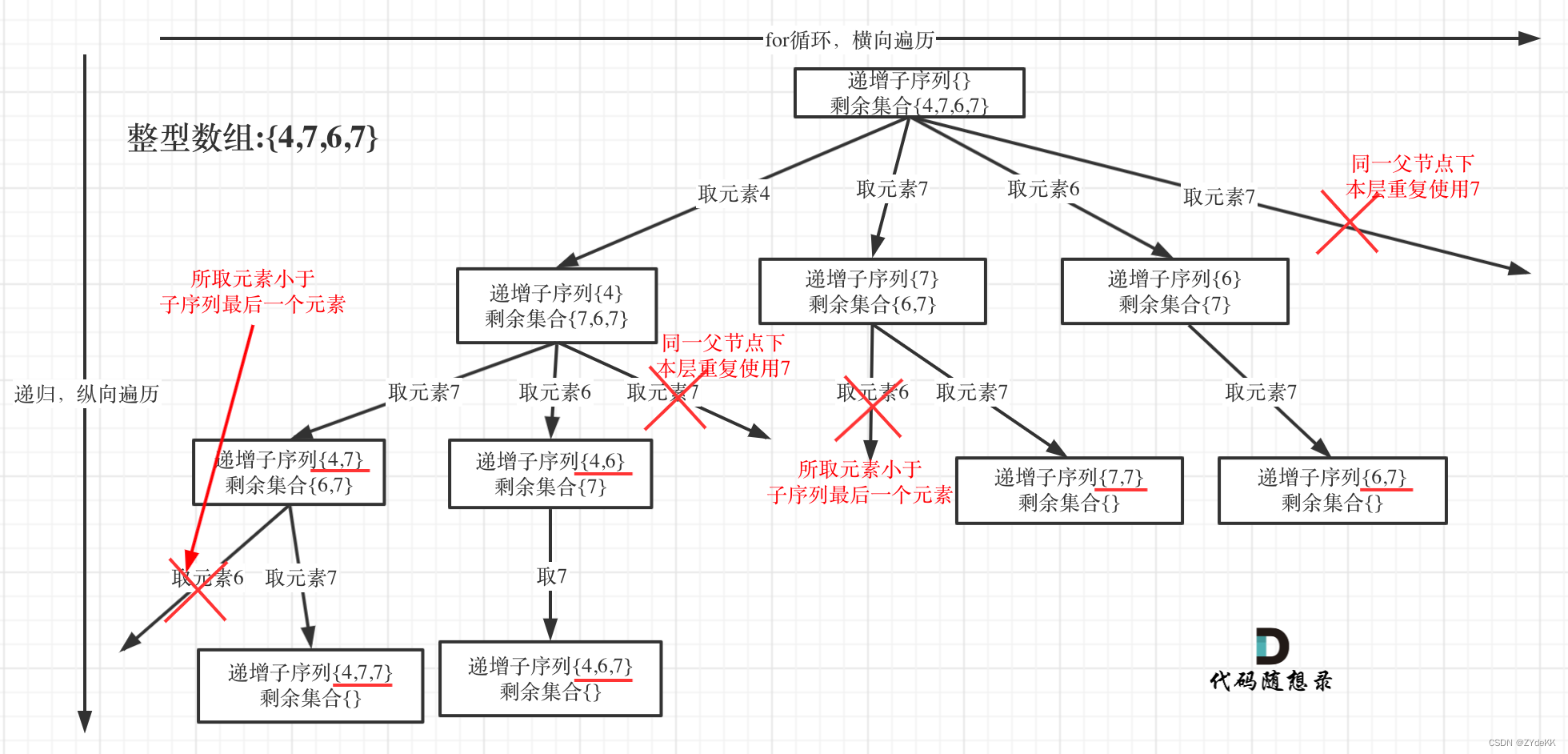
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:def backtrack(startIndex, path):used = set()for i in range(startIndex, len(nums)):# 如果元素小于path中的最后一个元素，无法构成递增# 如果元素已经在同一树层被使用过，则需要去重if (path and nums[i] < path[-1]) or nums[i] in used:continueused.add(nums[i])path.append(nums[i])# 收集符合条件的节点if len(path) > 1:result.append(path[:])backtrack(i + 1, path)path.pop()result = []backtrack(startIndex = 0, path = [])return result

46.全排列

排列问题和组合问题的区别在于，顺序不同算作不同排列。在组合问题中，我们定义 startIndex 确保每次递归只能向后探索，否则可能出现 [1, 2] 和 [2, 1] 这种重复组合。在排列问题中，我们不再需要 startIndex，只需确保同一元素不被重复选取。

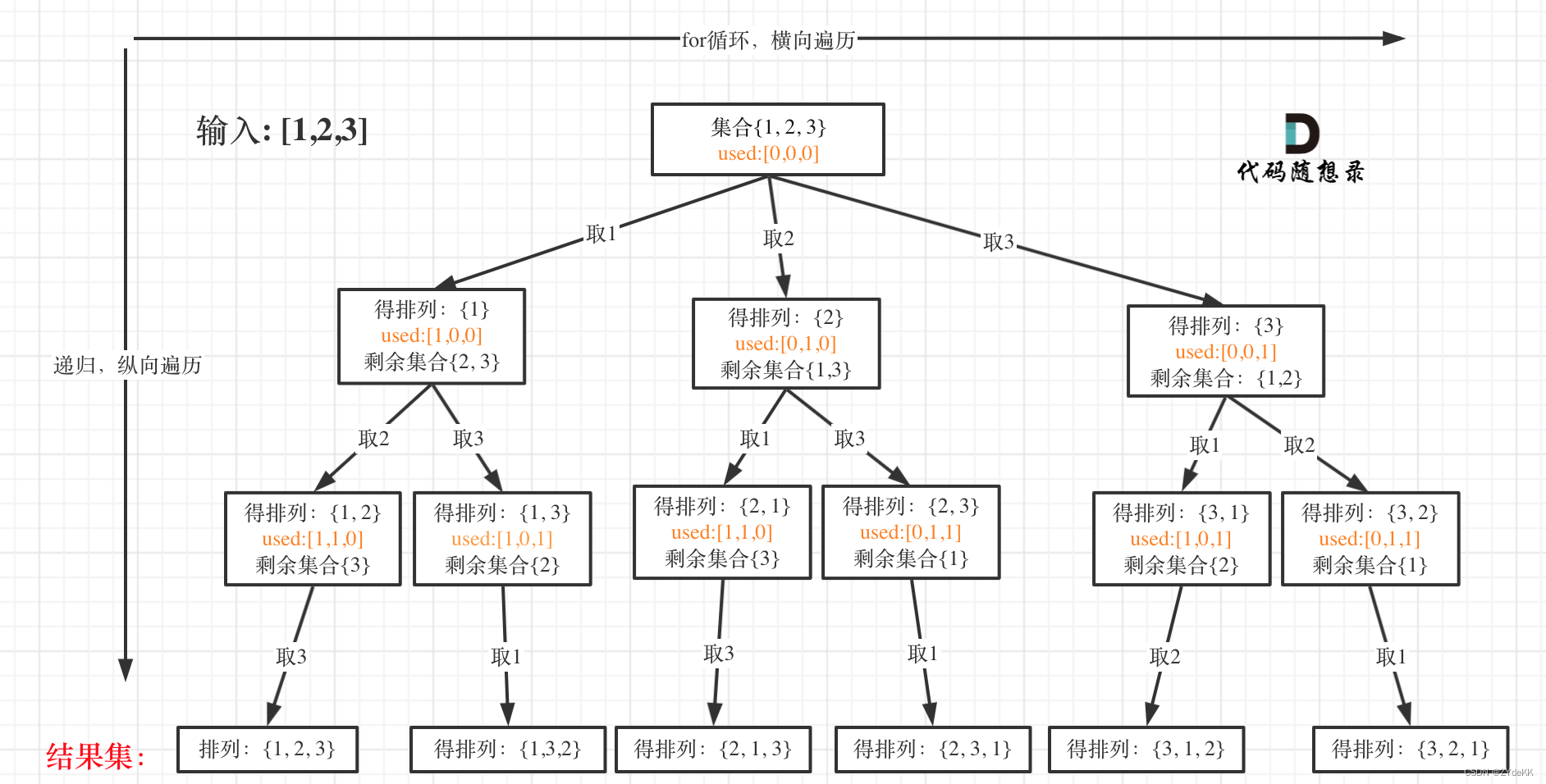
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:def backtrack(path):# 全排列在叶子结点处收集结果if len(path) == len(nums):result.append(path[:])returnfor i in range(len(nums)):# 只要同一元素不被重复选取# 顺序不同算作不同排列if nums[i] in path:continuepath.append(nums[i])backtrack(path)path.pop()result = []backtrack(path = [])return result

47.全排列II

本题多了一个存在重复数字的条件，因此为了确保同一元素不被重复选取，采用上一题的方法并不行。因为我们只是不能取同一元素，但如果两个元素的值相同呢？我们需要借助used数组 通过位置来判断而不是值。

class Solution:def permuteUnique(self, nums: List[int]) -> List[List[int]]:def backtrack(path, used):if len(path) == len(nums):result.append(path[:])returnfor i in range(len(nums)):# 避免同一元素被多次使用if used[i]:continue# 树层去重，由于 nums 包含重复数字，结果需要去重if i > 0 and nums[i] == nums[i-1] and used[i-1] == False:continueused[i] = Truepath.append(nums[i])backtrack(path, used)path.pop()used[i] = Falseresult = []nums.sort()backtrack(path = [], used = [False] * len(nums))return result