【NLP】关于Transformer模型的一些认知

一. Transformer模型简介

二. Transformer模型的架构

1. 编码器：

2. 解码器：

三. Transformer模型中残差连接层的作用

四. Transformer模型中, 输入部分的位置编码（PisitionalEncoding）矩阵为什么要使用三角函数对奇数列和偶数列做变换？

五. Transformer模型中掩码的应用

六. Transformer模型的优势（相比RNN类模型）

七. Transformer的并行化计算是怎么体现的？

八. Transformer模型的应用

一. Transformer模型简介

Transformer模型是深度学习领域中的一种革命性架构，尤其在自然语言处理（NLP）任务中产生了深远影响。该模型由谷歌的研究团队在2017年的论文《Attention is All You Need》中首次提出，完全摒弃了循环神经网络（RNN）和卷积神经网络（CNN），转而采用自注意力（Self-Attention）机制为核心构建而成。

二. Transformer模型的架构

如下图所示，Transformer模型的组成部分包括输入部分（Input）、编码器（Encoder）和解码器（Decoder）、输出部分（Output）四个部分，其中编码器和解码器均基于注意力机制设计：

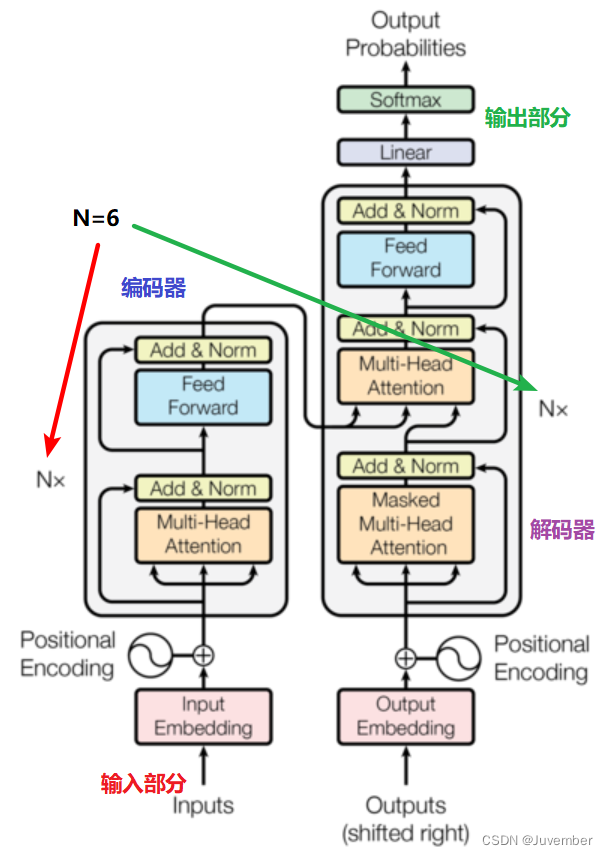
1. 编码器：

编码器由多个相同的层堆叠而成，每个层内部含有自注意力子层和前馈神经网络子层，以及残差连接（Residual Connections）和层归一化（Layer Normalization）。
自注意力机制使得模型能够在处理序列信息时同时考虑序列中所有元素之间的相互依赖关系，每个词都能够“关注”到序列中其他所有词，以便更好地理解上下文。

2. 解码器：

解码器同样由多层结构堆叠，每层也包括自注意力机制（但增加了遮蔽机制，防止未来信息泄露）、编码器-解码器注意力机制（Decoder-Encoder Attention），以及前馈神经网络子层等组件。
解码器不仅考虑输入序列的上下文信息，还能通过自注意力机制处理自身的序列信息，生成目标序列。

三. Transformer模型中残差连接层的作用

在Transformer模型中，残差连接（Residual Connections）扮演着至关重要的角色，它主要解决了以下几个关键问题：

梯度消失/梯度爆炸：在深度神经网络中，随着网络层数的增加，梯度在反向传播过程中可能逐渐减小（梯度消失），或者由于连乘效应而增大到不可控的程度（梯度爆炸）。这两种情况都会阻碍网络的有效训练。残差连接通过允许信息绕过非线性变换直接传递到下一层，使得模型能够更容易地学习恒等映射，即如果某一层没有学到任何东西，则至少可以通过学习“零”权重来保证输入不变，这样就可以缓解梯度消失问题。
简化优化过程：残差连接允许网络直接学习输入和输出之间的差异，而非从零开始构建完整的输出，这降低了模型的学习难度，提高了优化效率。
增强模型表达能力：即便在网络很深的情况下，残差连接也可以帮助保持信号的完整性，使得网络能够捕获更深层次的抽象特征，同时保持浅层特征的有效利用。

在Transformer模型架构中，每个多头自注意力子层（Multi-Head Self-Attention, MHA）和前馈神经网络子层（Position-wise Feed-Forward Networks, FFN）之后都会紧跟着一个残差连接，然后是一个层归一化（Layer Normalization）层。这样的设计确保了即使在网络深度增加时，信号仍然能够有效地在网络中流动，并且优化算法能够稳定地更新网络参数。

四. Transformer模型中, 输入部分的位置编码（PisitionalEncoding）矩阵为什么要使用三角函数对奇数列和偶数列做变换？

Transformer模型中，输入部分的位置编码矩阵采用三角函数（通常是正弦和余弦函数）来生成是因为这样的设计有助于模型捕捉序列中不同位置的相对或绝对位置信息，并且可以与嵌入向量以可学习的方式相结合，同时保持数值上的稳定性和平滑性。

具体来说，原始Transformer的位置编码方法将位置信息编码成向量的形式，通过以下公式生成位置编码向量P：

其中：

pos 是位置索引。
i 是位置编码向量的维度索引。
d_model 是模型的隐藏层维度大小。

这里采用奇数列和偶数列分别对应正弦和余弦函数的原因是利用了三角函数的周期性特征。通过调整频率（通过指数项控制），不同的维度会捕获不同频率的位置信号，从而允许模型学习不同尺度上的位置关系。这种编码方式使得模型能够区分相邻位置和较远位置的Token，并且当这些编码向量与词嵌入相加时，不会因为叠加而失去位置信息，因为三角函数在不同的位置上产生的值是不同的。

另外，这种方法保证了随着深度增加，位置编码不会因为多次线性变换而趋于零，从而解决了位置信息在深度网络中可能消失的问题。同时，由于正弦和余弦函数的值域在[-1, 1]之间，它们与词嵌入的元素值处于同一数量级，易于融合而不至于破坏原有输入信息的分布。

五. Transformer模型中掩码的应用

Transformer模型中的掩码主要应用于自回归序列建模任务，特别是在解码器部分的设计中。掩码的主要目的是确保在预测序列的当前位置时，模型只能访问到之前已经生成的词或位置信息，而不允许查看未来时刻的信息，这是自回归性质的要求。

1. 在Encoder部分：

在Encoder中，掩码主要用来处理输入序列中的填充（Padding）问题。由于输入序列通常会被填充到相同的长度，掩码张量会标记出哪些位置是实际的有效输入，哪些是填充的空位。这样，在计算Self-Attention时，模型就不会对填充的空位进行考虑，从而避免这些无意义的区域影响到有效输入的表示学习。

2. 在Decoder部分：

Decoder在训练和预测阶段都需要使用掩码来实现自回归性。在训练过程中，为了防止当前位置预测时参考到未来时刻的token，会对未来的tokens应用掩码，使得它们在当前时刻的注意力计算中被忽略，即其对应的attention权重置为0或者一个很小的负数（通常是在softmax操作前添加很大的负无穷，使对应的概率近似为0）。这样就确保了模型在预测序列中的下一个元素时只依赖于之前生成的元素，而不是尚未生成的后续元素。

总结来说，Transformer中的掩码是为了保证模型在处理变长序列以及进行自回归预测时遵循正确的数据流约束。

六. Transformer模型的优势（相比RNN类模型）

完全并行化计算，解决了RNN在处理长序列时的瓶颈，提高了训练速度；
自注意力机制能够有效捕获长距离依赖关系，比传统的RNN和CNN在某些情况下表现更好；
结构设计灵活，容易进行扩展和优化，例如通过堆叠更多的层或增加模型宽度来提升性能。

七. Transformer的并行化计算是怎么体现的？

在传统的循环神经网络（RNN）中，其核心特性是隐藏层状态的循环迭代，即每个时间步的计算都会依赖于前一个时间步的结果。这种递归性质意味着在训练过程中，我们必须按顺序逐个处理序列中的每个元素，无法同时计算整个序列的所有时间步。对于较长的序列，这种串行计算会导致显著的训练速度降低，因为GPU和其他并行硬件设备无法充分发挥它们并行计算的能力。

相反，Transformer模型抛弃了这种循环依赖的设计，引入了自注意力机制（Self-Attention），使得模型能够一次性对整个序列的所有元素进行并行计算。在自注意力机制中，每个位置的向量都可以直接参考序列中的任何其他位置，而不必等待之前的计算完成。这消除了序列长度对计算时间的影响，从而允许Transformer模型在训练和推理时充分利用并行计算资源（如GPU集群或TPU等），大大提升了处理长序列数据的效率和速度。