一、线性代数基础知识

本节将介绍简要地回顾一下部分基本线性代数内容，线性代数中的基本数学对象、算术和运算，并用数学符号和相应的代码实现来表示它们

1、标量

标量由只有一个元素的张量表示。 下面的代码将实例化两个标量，并执行一些熟悉的算术运算，即加法、减法、乘法、除法和指数。

import torch# 标量运算
x = torch.tensor(3.0)
y = torch.tensor(2.0)
# 加减乘除求幂
print(x + y, x - y, x * y, x / y, x ** y)

结果：

2、向量

向量可以被视为标量值组成的列表。 这些标量值被称为向量的元素（element）或分量（component）。
1.创建：人们通过一维张量表示向量。一般来说，张量可以具有任意长度，取决于机器的内存限制。

x = torch.arange(4)
x

2.使用：我们可以使用下标来引用向量的任一元素，例如可以通过Xi来引用第个元素。

x[3]

注意， 在数学中向量X可以写为：

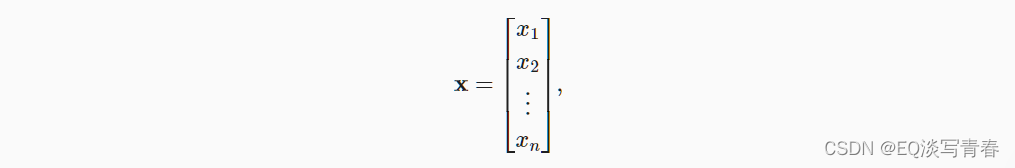
3.长度、维度和形状:向量只是一个数字数组，就像每个数组都有一个长度一样，每个向量也是如此。
与普通的Python数组一样，我们可以通过调用Python的内置len()函数来访问张量的长度。

len(x)

当用张量表示一个向量（只有一个轴）时，我们也可以通过.shape属性访问向量的长度。

x.shape

3、矩阵

正如向量将标量从零阶推广到一阶，矩阵将向量从一阶推广到二阶。在数学中，向量A可以写为：

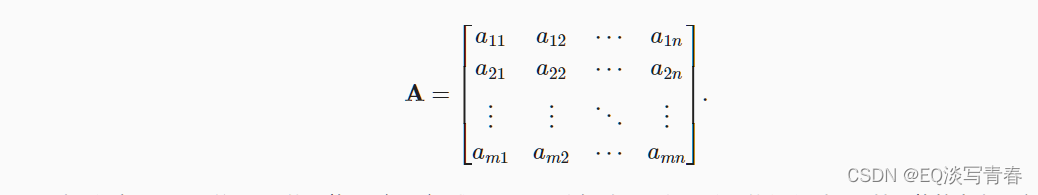
1.创建：当调用函数来实例化张量时， 我们可以通过指定两个分量
m和n来创建一个形状为的矩阵。

A = torch.arange(20).reshape(5, 4)
A

结果：

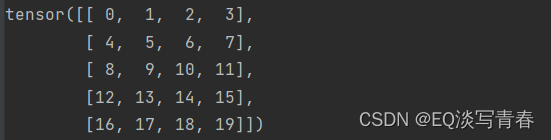
2.访问：我们可以通过行索引（i）和列索引（j）来访问矩阵中的标量元素Aij.

A[0][0]

3.转置：当我们交换矩阵的行和列时，结果称为矩阵的转置

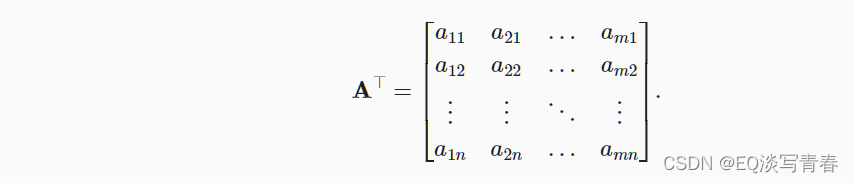
在代码中访问矩阵的转置

A.T

结果：

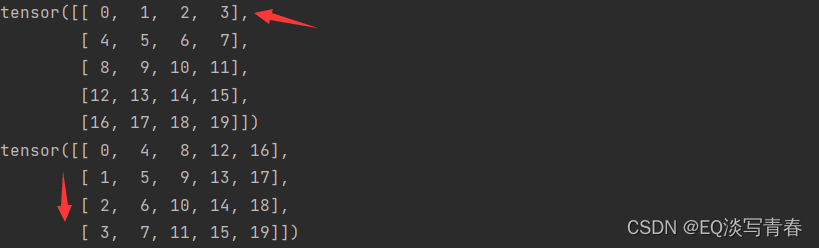
4、张量

就像向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构。 张量（本小节中的“张量”指代数对象）是描述具有任意数量轴的n维数组的通用方法。 例如，向量是一阶张量，矩阵是二阶张量。
1.创建：当调用函数来实例化张量时，

X = torch.arange(24).reshape(2, 3, 4)
X

结果：

2.张量算法的基本性质：标量、向量、矩阵和任意数量轴的张量（本小节中的“张量”指代数对象）有一些实用的属性。 例如，从按元素操作的定义中可以注意到，任何按元素的一元运算都不会改变其操作数的形状。 同样，给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量。

2.1矩阵相加：例如，将两个相同形状的矩阵相加，会在这两个矩阵上执行元素加法。

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

结果：

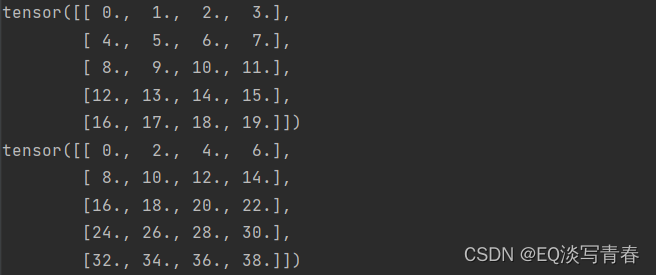
2.2矩阵的积：具体而言，两个矩阵的按元素乘法称为Hadamard积（Hadamard product），对应位置元素相乘，区别于矩阵乘法

A * B

结果：

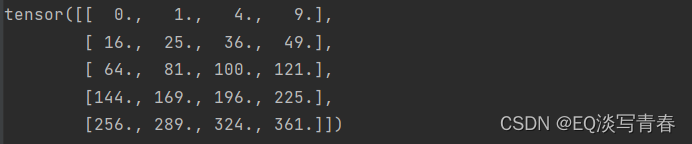
2.3矩阵每个元素加2：将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

5、点积

给定两个向量x,y， 它们的点积是相同位置的按元素乘积的和：

x = torch.ones(4, dtype = torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

结果：

6、向量—矩阵积

现在我们知道如何计算点积，可以开始理解矩阵-向量积，形如：

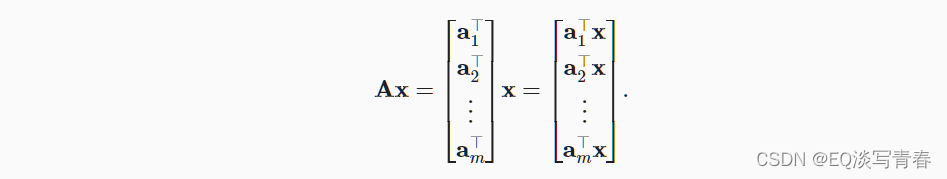
• 实现方法：

在代码中使用张量表示矩阵-向量积，我们使用mv函数。 当我们为矩阵A和向量x调用torch.mv(A, x)时，会执行矩阵-向量积。 注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。

#查看A是否可以与x相乘
A.shape, x.shape, torch.mv(A, x)

7、矩阵—矩阵乘法

在掌握点积和矩阵-向量积的知识后， 那么矩阵-矩阵乘法（matrix-matrix multiplication）应该很简单。

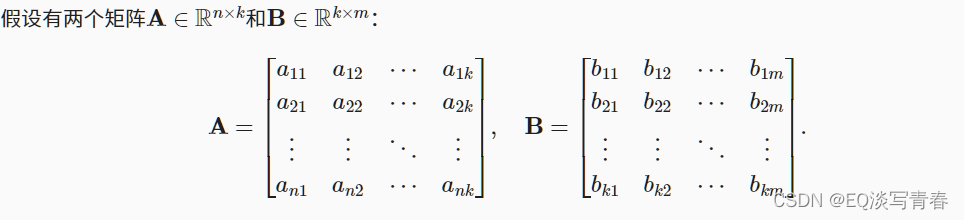
• 实现方法：

这里的A是一个5行4列的矩阵，B是一个4行3列的矩阵。 两者相乘后，我们得到了一个5行3列的矩阵。调用torch.mm(A, B)时，会执行矩阵-向量积:

A = torch.ones(5, 4)
B = torch.ones(4, 3)
torch.mm(A, B)

矩阵-矩阵乘法可以简单地称为矩阵乘法，不应与“Hadamard积”混淆。

二、小结

1. 标量、向量、矩阵和张量是线性代数中的基本数学对象。
2. 向量泛化自标量，矩阵泛化自向量。
3. 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
4. 一个张量可以通过sum和mean沿指定的轴降低维度。
5. 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。