abc339 E - Smooth Subsequence

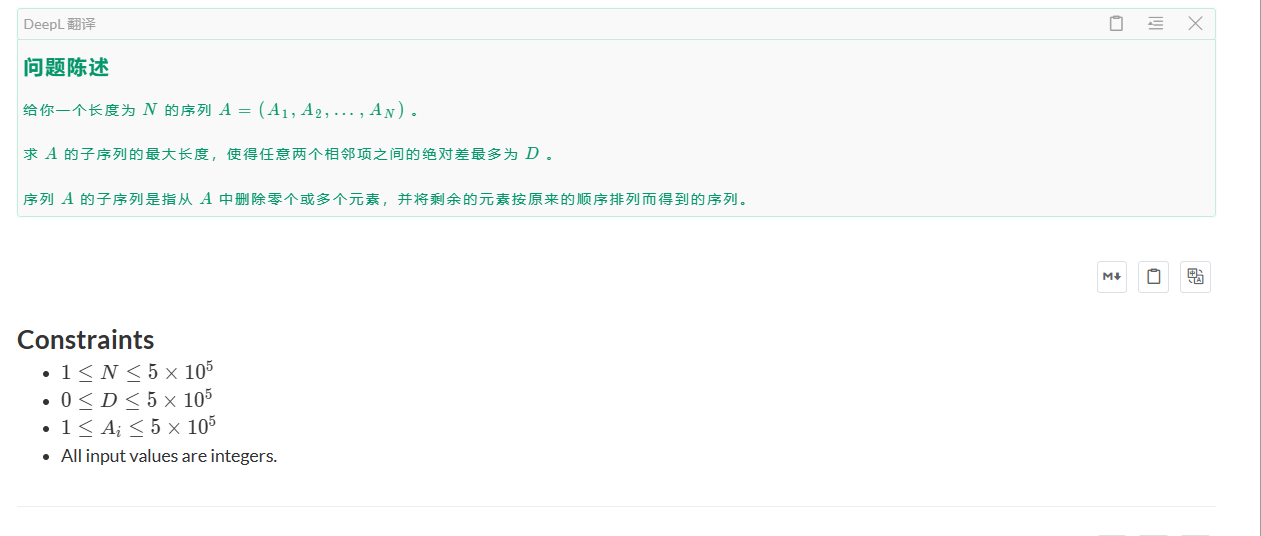
思路：我们很容想到一个$n$方的的状态转移方程，即对于每个i，我们去枚举$1$到$i-1$的状态，即
$$dp[i]=max(dp[i],dp[j]+1);$$
但是由于时间的限制，我们无法使用n方的dp去完成这道题目，考虑进行优化，因为对于状态$i$，其状态只能由前面点的状态转移过来，我们同样可以换一种说法，对于值$a[i]$，其状态只能由$(a[i]-d,a[i]+d)$这个范围内的数转移过来，我们想要长度最大，那么我们把值域当作下标进行维护，答案即为范围内的最大值，计算完当前状态后，我们再把当前的状态放入所谓的值域中。
对于上述操作，将值域看作下标后，其本质就是区间查询最大值，然后单点进行修改，因此线段树完全可以代替第二层循环，将时间复杂度降低到log级别。

#include <bits/stdc++.h>using namespace std;
const int N = 5e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<int, 5> ar;
int mod = 1e9+7;
// const int maxv = 4e6 + 5;
// #define endl "\n"int dp[N];
int a[N];struct node
{int l,r,val;#define l(x) tr[x].l#define r(x) tr[x].r#define val(x) tr[x].val
}tr[N*4];void update(int p)
{val(p)=max(val(p*2),val(p*2+1));
}void build(int p,int l,int r)
{if(l==r){tr[p]={l,r,0};return ;}l(p)=l,r(p)=r;int mid=(l+r)/2;build(p*2,l,mid),build(p*2+1,mid+1,r);
}void change(int p,int pos,int x)
{if(l(p)==r(p)){val(p)=x;return ;}int mid=(l(p)+r(p))/2;if(pos<=mid) change(p*2,pos,x);else change(p*2+1,pos,x);update(p);
}int query(int p,int l,int r)
{if(l<=l(p)&&r(p)<=r) return val(p);int mid=(l(p)+r(p))/2;int res=0;if(l<=mid) res=max(res,query(p*2,l,r));if(r>mid) res=max(res,query(p*2+1,l,r)); return res;
}void solve()
{int n,d;cin>>n>>d;for(int i=1;i<=n;i++){cin>>a[i];// dp[i]=1;}build(1,1,N);for(int i=1;i<=n;i++){int cur=query(1,max(0,a[i]-d),min(N,a[i]+d));dp[i]=cur+1;change(1,a[i],dp[i]);}cout<<query(1,1,N)<<endl;
} int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t=1;// cin>>t;while(t--){solve();}system("pause");return 0;
}