一、自注意力要解决什么问题

循环神经网络由于信息传递的容量以及梯度消失问题，只能建立短距离依赖关系。为了建立长距离的依赖关系，可以增加网络的层数或者使用全连接网络。但是全连接网络无法处理变长的输入序列，另外，不同的输入长度，其连接权重的大小也是不同的。注意力机制的优点在于它能够全局捕捉联系，不像序列RNN捕捉长期依赖关系的能力那么弱。另外，它可以并行化计算，且与CNN和RNN比较模型更简单、参数更少，适合轻量级应用。

解决问题一：处理变边长序列。自注意力机制实际上是注意力机制的一种，它也是一种网络的构型，它想要解决的问题是网络接收的输入是很多向量，并且向量的大小也是不确定的情况，比如机器翻译（序列到序列的问题，机器自己决定多少个标签），词性标注（Pos tagging 一个向量对应一个标签），语义分析（多个向量对应一个标签）等文字处理以及图像处理中。
解决问题二：动态地生成不同连接的权重。

二、自注意力模型怎么工作的

1、输入嵌入：首先，通过embedding将输入数据（如文本、图像等）转换为数值向量，即词嵌入或特征嵌入。这些嵌入向量将作为模型的输入。
2、自注意力计算：
2.1、生成查询、键和值：对于每一个输入嵌入向量（例如，每一个词向量），通过线性变换（或称为权重矩阵乘法）生成对应的查询向量（Query, Q）、键向量（Key, K）和值向量（Value, V）。这些变换通常是通过学习得到的权重矩阵来实现的。
2.2、计算注意力分数：使用查询向量和键向量计算注意力分数。这通常是通过点积（dot product）或缩放点积（scaled dot product）等方式实现的。这些分数反映了查询向量与每个键向量之间的相似性或相关性。
2.3、应用softmax函数：将注意力分数通过softmax函数进行归一化，映射到0-1，得到注意力权重。这样，每个键向量都会得到一个对应的权重值，这些权重值之和为1。
3、加权求和：
使用注意力权重对值向量进行加权求和，得到自注意力的输出。这个输出向量综合考虑了所有输入嵌入的信息，并根据它们与查询向量的相关性进行了加权。
4、前向传播与训练：
将自注意力的输出传递给模型的其他部分（如前馈神经网络等）进行进一步的处理和预测。然后，通过反向传播算法和优化器来更新模型的权重，以最小化在特定任务上的损失函数。

二、自注意力计算的几个关键点

训练得到权重矩阵，权重矩阵和输入数据计算得出Q、K、V，Q和K得到注意力权重，注意力权重和值向量生成输出。

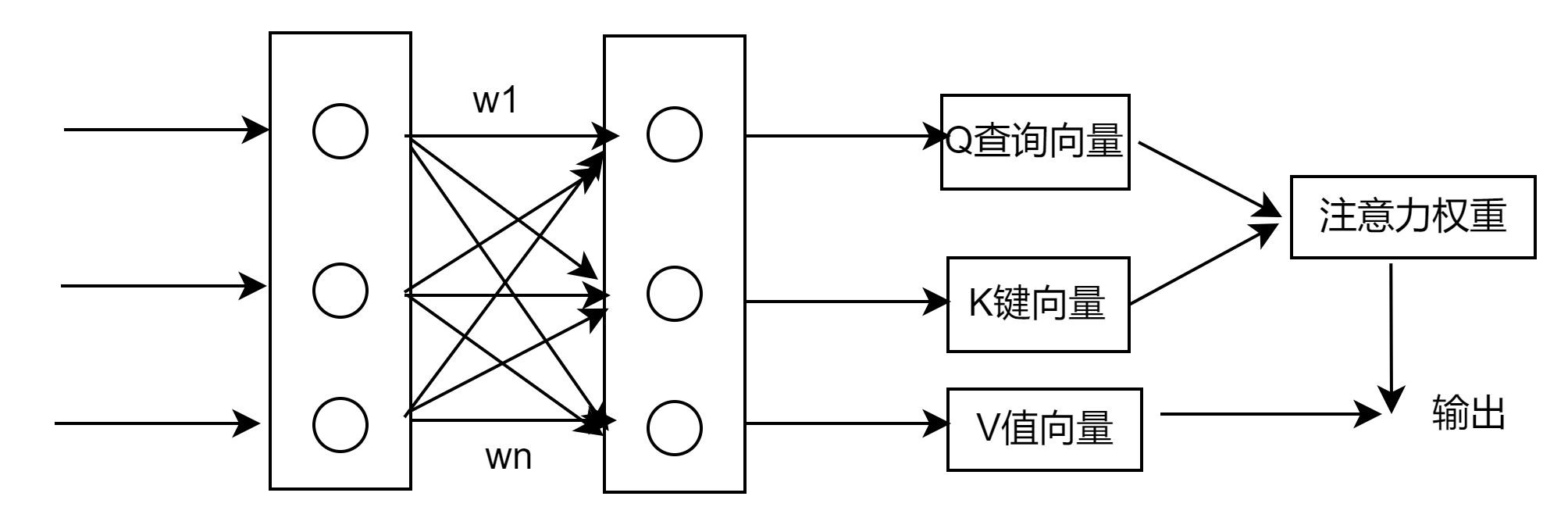
1、Q、K、V是什么

在注意力机制中，Q（查询向量）、K（键向量）和V（值向量）是核心概念，它们共同协作来计算注意力权重，进而决定模型在给定任务中应关注哪些信息。这种机制尤其在序列模型、自然语言处理和图像处理等领域中广泛应用。下面，我将详细解释这三个向量的含义和作用。

查询向量（Query, Q）：

含义：查询向量通常代表当前需要关注或查询的信息。在序列模型中，它可能表示当前位置的隐状态或者一个待处理的词或特征。
作用：查询向量用于与键向量进行比较，以确定哪些键与当前查询最相关。这种比较通常通过计算点积、余弦相似度或其他形式的相似度度量来完成。
键向量（Key, K）：

含义：键向量是数据集中用于与查询向量进行匹配的部分。在序列模型中，键向量可能表示数据序列中每个位置的隐状态或特征。
作用：键向量提供了用于与查询向量进行比较的信息。通过比较查询向量和键向量，模型可以判断哪些部分的数据与当前的查询最为相关。
值向量（Value, V）：

含义：值向量包含实际的信息，这些信息将被用于生成最终的输出。在序列模型中，值向量可能表示与键向量相关联的隐藏状态或特征。
作用：一旦模型通过查询向量和键向量确定了哪些部分的数据与当前查询相关，它就会使用这些相关的值向量来生成输出。这通常是通过计算注意力权重，然后将这些权重应用于值向量来实现的。
工作原理：

注意力机制的核心思想是，根据查询向量与所有键向量的相似度，为每个值向量分配一个注意力权重。这些权重决定了在生成输出时，每个值向量应该被考虑的程度。具体来说，计算过程通常包括以下几个步骤：

计算查询向量与每个键向量的相似度（例如，通过点积）。
将相似度分数通过某种方式（如softmax函数）转换为注意力权重，确保所有权重的和为1。
使用这些权重对值向量进行加权求和，得到最终的输出。
通过这种方式，注意力机制允许模型在处理数据时动态地关注最相关的信息，从而提高模型的性能和准确性。

2、Q、K、V是怎么得到的

Q（查询向量）、K（键向量）和V（值向量）的值在注意力机制中是通过一系列线性变换和权重矩阵从输入数据中得到的。这些线性变换允许模型捕捉输入数据的不同方面，并为后续的注意力计算提供必要的表示。

具体来说，Q、K、V通常是从输入序列（如文本中的单词或图像中的特征）的嵌入向量（embedding vectors）中计算得出的。嵌入向量是将原始输入（如单词或像素）转换为固定大小的向量表示，以便模型能够处理。

在自注意力（self-attention）机制中，如Transformer模型所使用的，对于输入序列中的每个元素（例如，一个单词或一个特征），都会执行以下步骤来得到Q、K、V：

定义权重矩阵：首先，需要定义三个权重矩阵(W_Q)、(W_K)和(W_V)，它们分别用于计算查询向量、键向量和值向量。

线性变换：对于输入序列中的每个元素的嵌入向量(x_i)，分别计算其与权重矩阵的乘积：

(Q_i = x_i \times W_Q)
(K_i = x_i \times W_K)
(V_i = x_i \times W_V)
这些乘法操作实际上是线性变换，它们将输入嵌入向量转换为新的向量空间，从而得到Q、K、V的表示。

多头注意力（可选）：在Transformer等模型中，为了提高模型的表达能力，通常会采用多头注意力（Multi-Head Attention）机制。这意味着会有多组Q、K、V的权重矩阵，分别对应不同的“头”。每个头都会独立地计算一组Q、K、V，并在后续的注意力计算中发挥作用。

注意力权重计算：一旦得到了Q、K、V，就可以通过计算Q和K之间的相似度（如点积）来得到注意力权重。这些权重表示了输入序列中不同位置之间的相对重要性。

加权求和：最后，使用注意力权重对V进行加权求和，得到当前位置的注意力输出。这个输出综合考虑了输入序列中所有位置的信息，但根据注意力权重进行了加权，以突出与当前位置最相关的信息。

通过这个过程，Q、K、V的值是从输入数据中动态计算得出的，并且它们共同协作以实现注意力机制的功能，使模型能够关注输入中最重要的部分。

3、计算Q、K、V的权重矩阵是怎么来的

定义权重矩阵是注意力机制中的关键步骤之一，它允许模型学习如何从输入数据中提取和转换信息以生成查询向量（Q）、键向量（K）和值向量（V）。下面我将详细解释权重矩阵的定义和它们在计算Q、K、V中的作用。

定义权重矩阵
在注意力机制中，权重矩阵是一组可学习的参数，它们通过反向传播算法在训练过程中被优化，以最小化模型在特定任务上的损失函数。权重矩阵的初始值通常是随机初始化的，并在训练过程中逐渐调整以捕捉输入数据的复杂结构和模式。

对于查询向量（Q）、键向量（K）和值向量（V），我们分别定义三个权重矩阵：(W_Q)、(W_K) 和 (W_V)。这些矩阵的维度通常根据模型的具体实现和输入数据的特性来设定。

(W_Q)：用于计算查询向量（Q）的权重矩阵。它将输入嵌入向量映射到查询向量空间。
(W_K)：用于计算键向量（K）的权重矩阵。它将输入嵌入向量映射到键向量空间。
(W_V)：用于计算值向量（V）的权重矩阵。它将输入嵌入向量映射到值向量空间。
线性变换
一旦定义了权重矩阵，我们就可以对输入序列中的每个元素的嵌入向量进行线性变换，以得到对应的Q、K、V向量。

假设我们有一个输入序列，其中每个元素（例如，一个单词或一个特征）都有一个对应的嵌入向量 (x_i)。这个嵌入向量可能是一个固定大小的实数向量，其中包含了该元素在特定上下文中的表示信息。

线性变换的过程可以表示为将嵌入向量 (x_i) 与相应的权重矩阵相乘：

查询向量（Q）：(Q_i = x_i \times W_Q)
键向量（K）：(K_i = x_i \times W_K)
值向量（V）：(V_i = x_i \times W_V)
这里，“(\times)” 表示矩阵乘法。嵌入向量 (x_i) 是一个列向量，而 (W_Q)、(W_K) 和 (W_V) 是权重矩阵。这些乘法操作将 (x_i) 转换到新的向量空间，生成对应的Q、K、V向量。

权重矩阵的作用
权重矩阵在注意力机制中起到了关键作用。通过调整这些矩阵中的参数，模型可以学习如何从输入数据中提取有用的信息，并将其转换为适用于注意力计算的表示形式。
捕捉不同方面的信息：权重矩阵允许模型捕捉输入数据的不同方面。通过学习不同的线性变换，模型可以关注输入中的不同特征或模式，并将它们分别映射到Q、K、V向量空间中。
学习注意力分布：通过计算Q和K之间的相似度（如点积），模型可以学习输入序列中不同位置之间的相对重要性。这种学习到的注意力分布使得模型能够动态地关注与当前任务最相关的信息。
优化模型性能：权重矩阵是通过反向传播和梯度下降等优化算法进行训练的，以最小化模型在特定任务上的损失函数。通过调整这些矩阵中的参数，模型可以逐渐改进其性能，并在处理新数据时更好地应用注意力机制。