主页:(*´∇`*) 咦,又好了~ xiaocr_blog
算法概述:递归算法是一种直接或者间接调用自身函数或者方法的算法。说简单了就是程序自身的调用。
算法实质:递归算法就是将原问题不断分解为规模缩小的子问题,然后递归调用方法来表示问题的解。(用同一个方法去解决规模不同的问题)
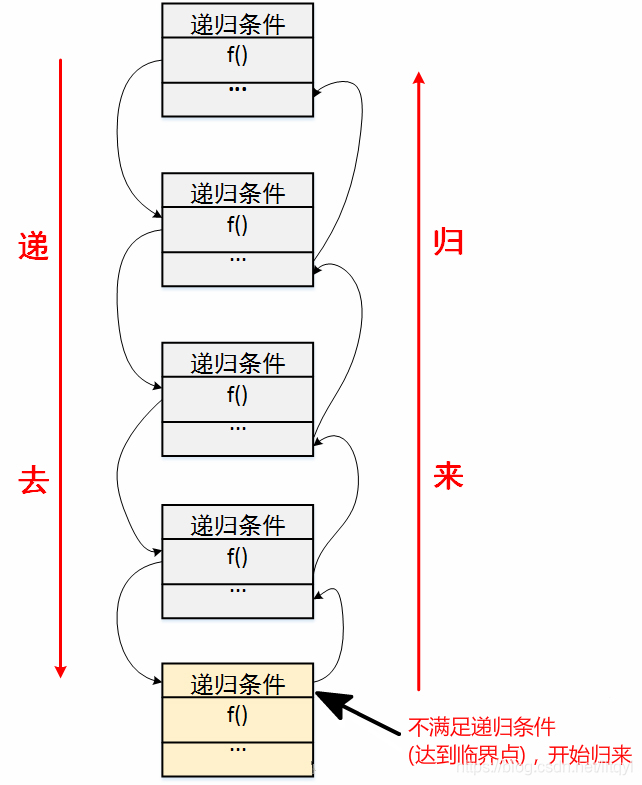
算法思想:递归算法,顾名思义就是有两个大的阶段:递和归,即就是有去(递去)有回(归来)。
算法设计要素:
- 明确递归的终止条件
- 提取重复的逻辑,缩小问题的规模不断递去
- 给出递归终止时的处理办法
·例题1:简单累和
#include<bits/stdc++.h>
using namespace std;
int get_sum(int n) {if (n == 1) {return 1;}return get_sum(n - 1) + n;
}
int main() {int n;cin >> n;cout << "Sum=" << get_sum(n) << endl;return 0;
}·例题2:设有n个数已经按从小到大的顺序排列,现在输入x,判断它是否在这n个数中,如果存在则输出“YES",否则输出”NO“
#include<bits/stdc++.h>
using namespace std;
int a[101], k;
void search(int a[], int left, int right) {if(left<right){int mid = (left + right) / 2;if (a[mid] == k) { cout << "YES"; return; }else if (k < a[mid]) { search(a, mid + 1, right); }else{ search(a, left, mid); }}else {cout << "NO" << endl;}
}
int main() {int n;cin >> n >> k;for (int i = 1; i <= n; i++) {cin >> a[i];}search(a, 1, n);return 0;
}·例题3:Hanoi汉诺塔问题
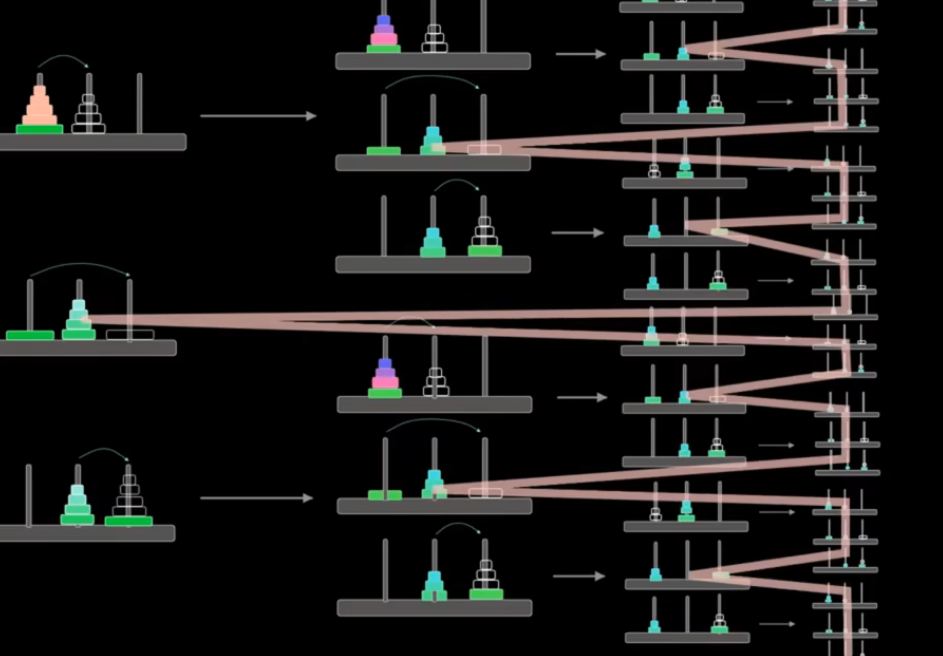
#include<bits/stdc++.h>
using namespace std;
void move(char pos1, char pos2) {printf("%c-->%c", pos1, pos2);
}
void Hanoi(int n, char pos1, char pos2, char pos3) {if (n == 1) {move(pos1, pos3);cout << "\n";}else {Hanoi(n - 1, pos1, pos3, pos2);move(pos1, pos3);cout << "\n";Hanoi(n - 1, pos2, pos1, pos3);}}
int main() {int n;cin >> n;Hanoi(n, 'A', 'B', 'C');return 0;
}
·例题4:斐波那契数列
#include<bits/stdc++.h>
using namespace std;
int f(int n) {if (n == 1 || n == 2) { return 1; }else {return (f(n - 1) + f(n - 2));}
}
int main() {int n;cin >> n;cout << f(n);return 0;
}
·例题五:集合的划分
描述
设S是一个具有n个元素的集合,S=〈a1,a2,……,an〉,现将S划分成 k 个满足下列条件的子集合S1,S2,……,Sk,且满足:
1.Si≠∅
2.Si∩Sj=∅ ( 1≤i,j≤k,i≠j )
3.S1∪S2∪S3∪…∪Sk=S
则称S1,S2,……,Sk是集合S的一个划分。它相当于把S集合中的n个元素a1,a2,……,an放入k个(0<k≤n<30)无标号的盒子中,使得没有一个盒子为空。请你确定n个元素a1,a2,……,an 放入k个无标号盒子中去的划分数S(n,k)。
【输入】
给出n和k。
【输出】
n个元素a1,a2,……,an 放入k个无标号盒子中去的划分数S(n,k)。

#include<bits/stdc++.h>
using namespace std;
int S(int n, int k) {if (n < k || k == 0) { return 0; }if (k == 1 || k == n) { return 1; }return (S(n - 1, k - 1) + k * S(n - 1, k));
}int main() {int n, k;cin >> n >> k;cout << S(n, k);return 0;
}·例题六:数的计数
描述
我们要求找出具有下列性质数的个数(包括输入的自然数n)。先输入一个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:
不作任何处理;
在它的左边加上一个自然数,但该自然数不能超过原数的一半;
加上数后,继续按此规则进行处理,直到不能再加自然数为止。
#include<bits/stdc++.h>
using namespace std;
int ans;
void f(int n) {ans++;for (int i = 1; i <= n/2; i++) {f(i);}
}
int main() {int n;cin >> n;f(n);cout << ans;return 0;
}习题:
全排列
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。
我们假设对于小写字母有‘a’ <‘b’ < ... <‘y’<‘z’,而且给定的字符串中的字母已经按照从小到大的顺序排列。
【输入】
只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在1到6之间。
【输出】
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。字母序如下定义:
已知S=s1s2...sk,T=t1t2...tkS=s1s2...sk,T=t1t2...tk,则S<T等价于,存在p(1<=p<=k),使得s1=t1,s2=t2,...,sp−1=tp−1,sp<tps1=t1,s2=t2,...,sp−1=tp−1,sp<tp成立。
#include<bits/stdc++.h>
using namespace std;
char a[10], ans[10];
bool v[10];
int len;
void f(int pos) {if (pos == len) { for (int i = 0; i < len; i++) {cout << ans[i];}cout << endl;return; }else {for (int i = 0; i < len; i++) {if(v[i]==0){v[i] = 1;ans[pos] = a[i];f(pos + 1);v[i] = 0;}}}
}
int main() {cin >> a;len = strlen(a);f(0);return 0;
}分解因数
题目描述】给出一个正整数aa,要求分解成若干个正整数的乘积,即a=a1×a2×a3×...×an,并且1<a1≤a2≤a3≤...≤an,问这样的分解的种数有多少。注意到a=a也是一种分解。
#include<bits/stdc++.h>
using namespace std;
int a,n,ans;
void f(int a, int k) {if (k >= a) { return; }for (int i = k; i <= a / i; i++) {if (a % i == 0) {ans++;f(a / i, i);}}
}
int main() {cin>> n;//n代表测试组数while (n--) {cin >> a;ans = 1;f(a, 2);cout << ans << endl;}return 0;
}pell数列
【题目描述】
Pell数列a1,a2,a3,...的定义是这样的,a1=1,a2=2,...,an=2an−1+an−2(n>2)。
给出一个正整数 k,要求Pell数列的第 k项模上 32767
是多少。
【输入】
第1行是测试数据的组数 n,后面跟着 n行输入。每组测试数据占 1行,包括一个正整数k(1≤k<1000000)。
#include<bits/stdc++.h>
using namespace std;
int pell(long long n) {if (n == 1) { return 1; }if (n == 2) { return 2; }return (2 * pell(n - 1) + pell(n - 2));
}
int main() {int n;cin >> n;while(n--){int k;cin >> k;cout << pell(k) % 32767 << endl;}return 0;
}爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
#include<bits/stdc++.h>
using namespace std;
int palouti(int n) {if (n == 1) { return 1; }if (n == 2) { return 2; }return palouti(n - 1) + palouti(n - 2);}
int main() {int n;while (cin >> n) {cout << palouti(n) << endl;}return 0;
}放苹果
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
【输入】
第一行是测试数据的数目t(0<=t<=20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
【输出】
对输入的每组数据M和N,用一行输出相应的K。
/*
递归边界:盘子数目和苹果数目相同||盘子数目就一个
第一种情况:盘子数目比苹果数目多-->多出来的盘子数无用
第一种可转换为第二种
第二种情况:苹果数目大于等于盘子数目-->也分为两种情况:有盘子空余和无盘子空余
*/
#include<bits/stdc++.h>
using namespace std;
int apple, plate;
int f(int apple, int plate) {if (apple == 0|| plate == 1) { return 1; }if (plate > apple) { return f(apple, apple); }if (apple >= plate) {return f(apple, plate - 1) + f(apple - plate, plate);}
}
int main() {cin >> apple >> plate;cout<<f(apple, plate);return 0;
}
求最大公约数
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b){return b == 0 ? a : gcd(b, a % b);
}
int main() {int a, b;cin >> a >> b;cout << gcd(a, b);return 0;
}2的幂次方表示
任何一个正整数都可以用2的幂次方表示。例如:
137=27+23+20
同时约定方次用括号来表示,即ab可表示为a(b)。由此可知,137可表示为:
2(7)+2(3)+2(0)
进一步:7=22+2+20(21用2表示)
3=2+20
所以最后137可表示为:
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:
1315=210+28+25+2+1
所以1315最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
#include<bits/stdc++.h>
using namespace std;
void f(int n) {int c = 0;while (pow(2, c)<=n) {c++;}c--;if (c == 0) {cout << "2(" << c << ")";}else if (c == 1) {cout << "2(" << c << ")";}else {cout << "2(";f(c);cout<< ")";}int other = n - pow(2, c);if (other) {cout << "+";f(other);}}
int main() {int num;cin >> num;f(num);}分数求和
#include<bits/stdc++.h>
using namespace std;
int gcd(int n, int m) {return m == 0 ? n : gcd(m, n % m);
}
int main() {int a, b, c, d, e, f, n;scanf_s("%d%d/%d", &n, &a, &b);for (int i = 2; i <= n; i++) {scanf_s("%d/%d", &c, &d);e = (b * d) / gcd(b, d);a *= e / b; b = e;a += c * (e / d);}int k = gcd(a, b);if (a % k == 0) {printf("%d/%d", a / k, b / k);}else {printf("%d/%d", a, b);}return 0;
}因子分解
#include<bits/stdc++.h>
using namespace std;
void fact(int n, int a) {int b = 0;while (n == 0 || a > n) {return;}while (n % a == 0) {b++;n /= a;}if (b >= 1) {if (b == 1) {printf("%d", a);}else {printf("%d^%d", a, b);}if (n > a) {cout << "*";}}fact(n , a + 1);
}
int main() {int n;cin >> n;fact(n,2);}JetsonNano 安装开机问题屏幕进不去】)




——基本线条操作)









)
)


