本专栏内容为：递归，搜索与回溯算法专栏。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：递归搜索回溯专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目来源

本题来源为：

Leetcode 814. 二叉树剪枝

题目描述

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

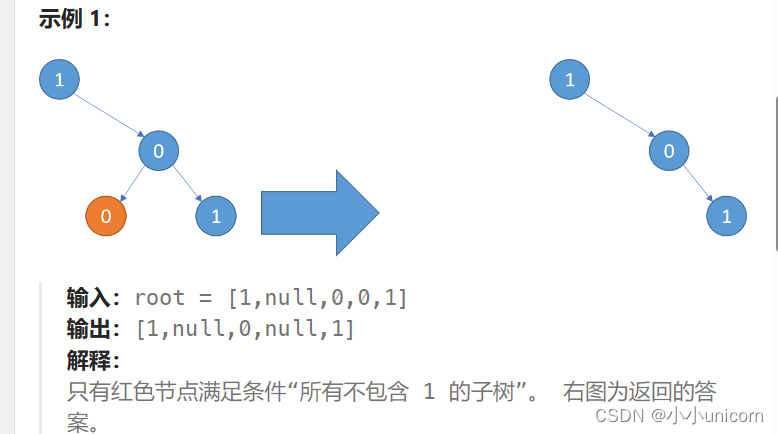
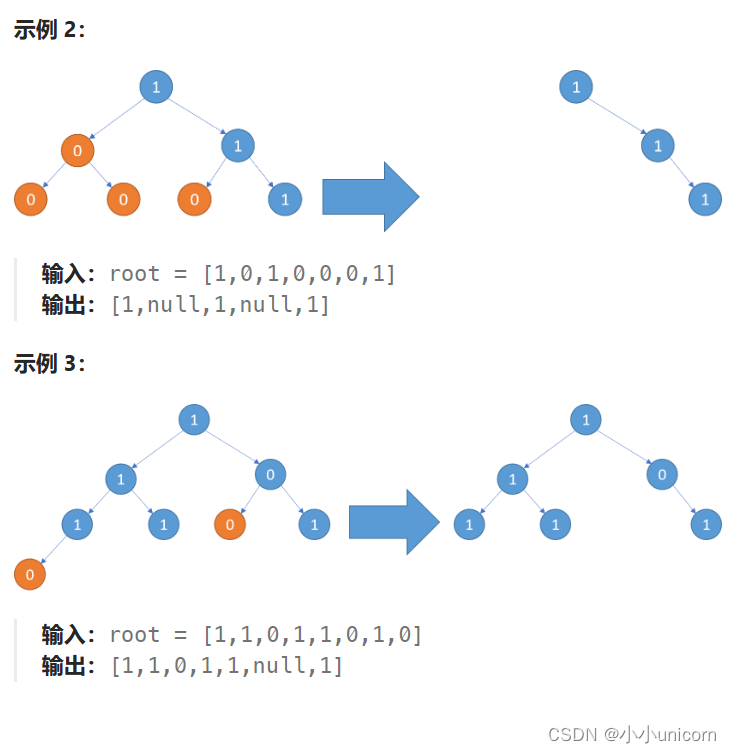
题目解析

把题目给的示例分析一下：

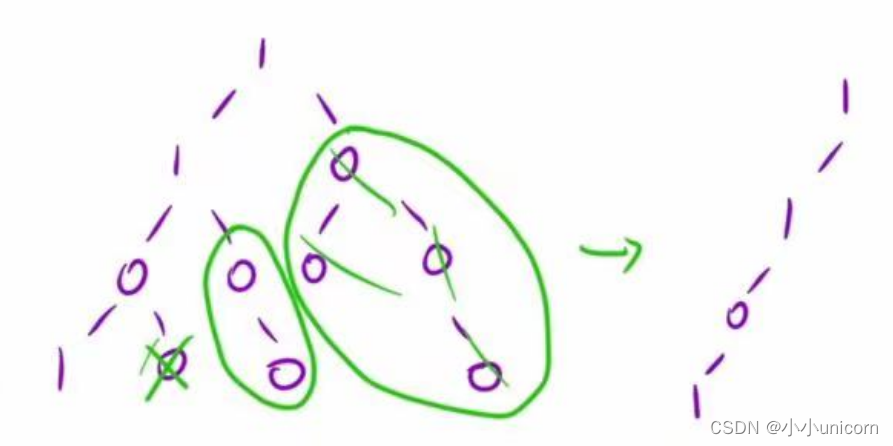
题目说返回移除了所有不包含 1 的子树的原二叉树。换句话是就是将二叉树中全是0的子树删除掉。

算法原理

对于碰到特别抽象的问题时，也就是说子问题很难发现时，我们可以通过决策树，抽象出递归的三个核心问题。

对于本题的子问题也还是很好想的，就是传一个根，将这个全部包含0的节点干掉，然后返回新的头指针。

以绿色这一层为例：要想将这一层剪枝，必须得让这个节点的左子树和右子树都为0时才能剪枝。那么肯定是后序遍历。

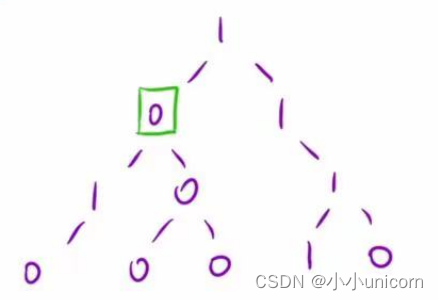
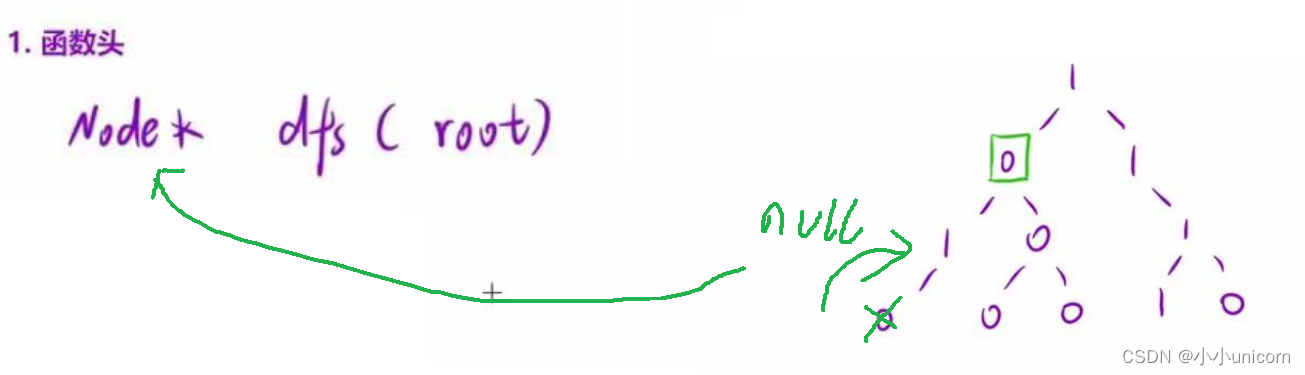
先看左下角这个节点，他的左右节点都为空，那么这个我们就可以把它干掉。那干掉了这个节点返回1节点时，1节点的左节点是不是要置空，那么怎么让他回去的时候将节点指向空呢？加一个返回值即可。当返回的时候把null给他。那么咱们得函数头肯定是有一个返回值的：

依次内推，继续模拟这个过程：

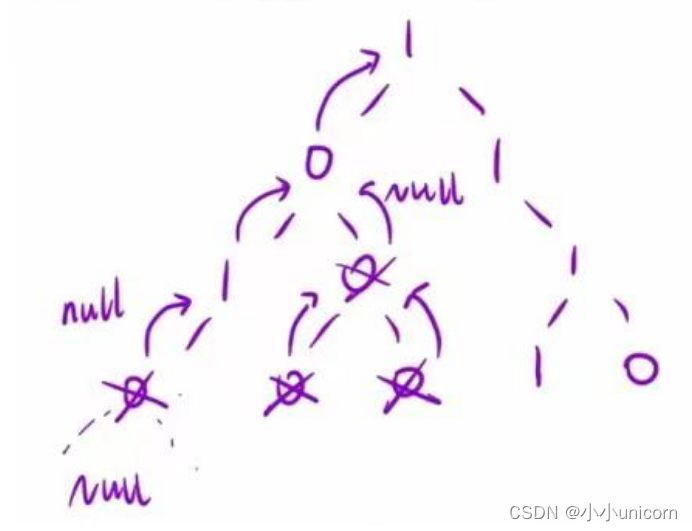
注意要是节点不用剪枝时，但也要向上返回时，就要返回此节点的值，要和函数头保持一致。

那么我们的函数体和出口已经出来了：

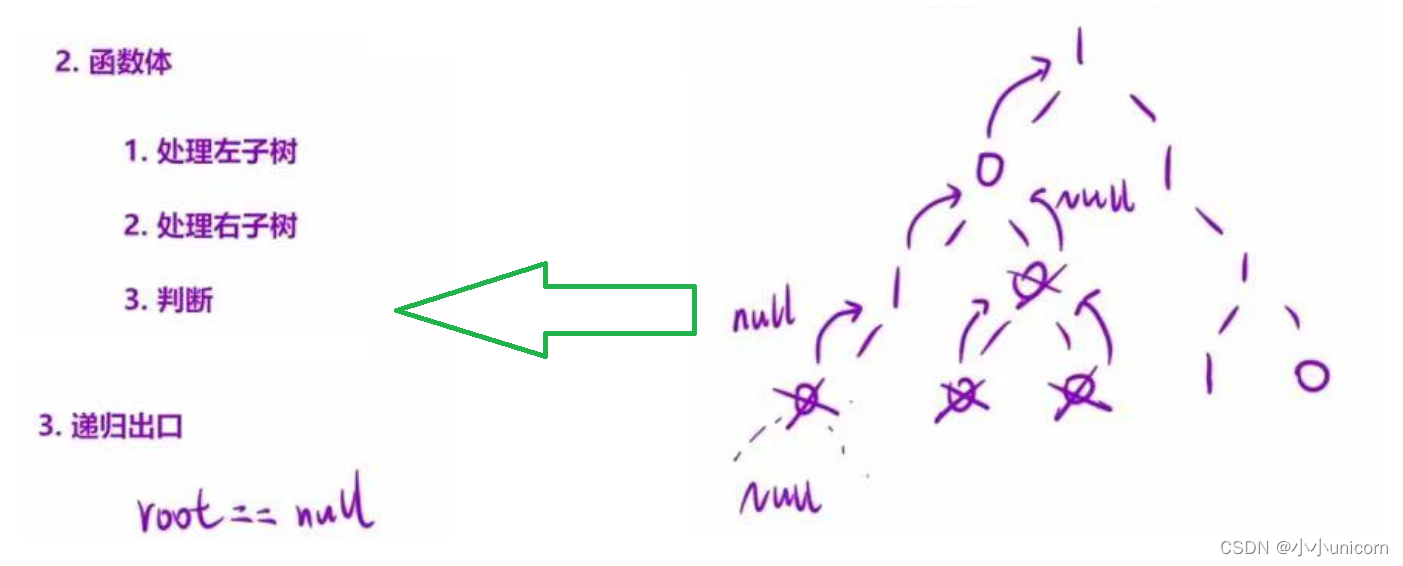
代码实现

如果笔试的话，可以不用delete,但是要是面试，可以问一下面试官节点是不是一个一个new出来的，要是New出来的很可能就会报错。

class Solution 
{
public:TreeNode* pruneTree(TreeNode* root) {if(root==nullptr)return nullptr;root->left=pruneTree(root->left);root->right=pruneTree(root->right);if(root->left==nullptr&&root->right==nullptr&&root->val==0){delete root;//防止内存泄漏root=nullptr;}return root;}
};