可选实验室：神经元和层

实验室将探索神经元和层的内部工作原理，特别是将课程1中掌握的模型，即回归/线性模型和逻辑斯蒂模型，与之进行对比。本实验室将介绍Tensorflow并演示这些模型是如何在该框架中实现的。

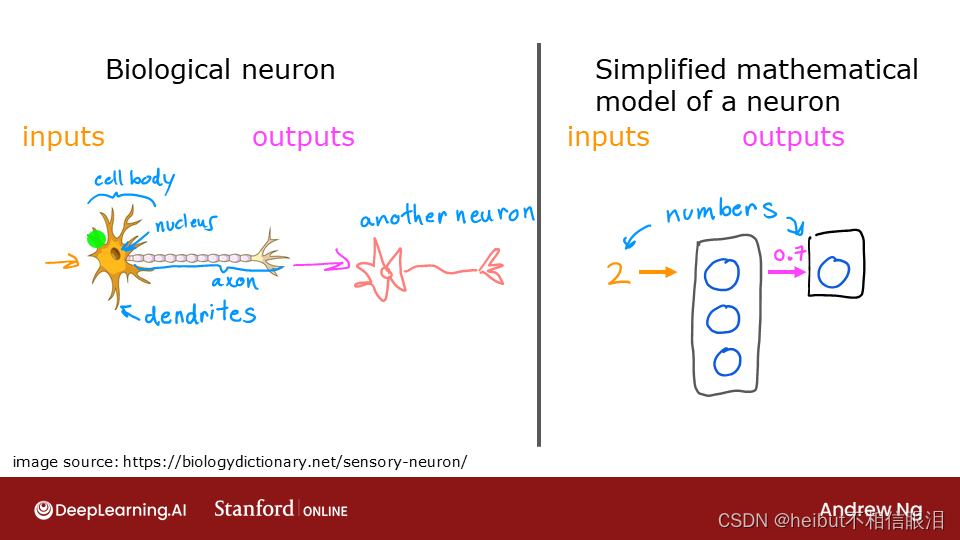
包

Tensorflow和Keras
Tensorflow是谷歌开发的机器学习包。2019年，谷歌将Keras集成到Tensorflow中，并发布了Tensorflow 2.0。Keras是一个由franois Chollet独立开发的框架，它为Tensorflow创建了一个简单的、以层为中心的接口。本课程将使用Keras接口。

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras import Sequential
from tensorflow.keras.losses import MeanSquaredError, BinaryCrossentropy
from tensorflow.keras.activations import sigmoid
from lab_utils_common import dlc
from lab_neurons_utils import plt_prob_1d, sigmoidnp, plt_linear, plt_logistic
plt.style.use('./deeplearning.mplstyle')
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)

后两行代码的含义是设置 TensorFlow 的日志级别，将 TensorFlow 的日志级别设置为 ERROR 级别，从而只记录 ERROR 级别及以上的日志信息，不记录更低级别的日志信息。
另外，tf.autograph.set_verbosity(0)这行代码是设置 AutoGraph 的日志级别，将 AutoGraph 的日志级别设置为 0，表示不输出任何日志信息。 AutoGraph 是 TensorFlow 中用于将普通 Python 代码转换成 TensorFlow 计算图的工具，设置日志级别为 0 可以关闭 AutoGraph 的日志输出，减少不必要的输出信息。

无激活神经元-回归/线性模型

数据集
我们将使用课程一的例子，房价的线性回归。

X_train = np.array([[1.0], [2.0]], dtype=np.float32)           #(size in 1000 square feet)
Y_train = np.array([[300.0], [500.0]], dtype=np.float32)       #(price in 1000s of dollars)fig, ax = plt.subplots(1,1)
ax.scatter(X_train, Y_train, marker='x', c='r', label="Data Points")
ax.legend( fontsize='xx-large')
ax.set_ylabel('Price (in 1000s of dollars)', fontsize='xx-large')
ax.set_xlabel('Size (1000 sqft)', fontsize='xx-large')
plt.show()

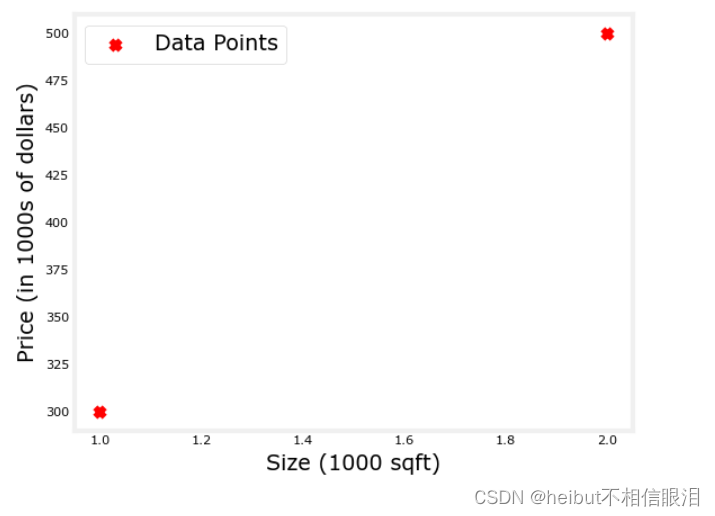
回归/线性模型
未激活的神经元实现的函数与课程1线性回归相同:

我们可以用一个神经元或单元定义一个层，并将其与熟悉的线性回归函数进行比较。

linear_layer = tf.keras.layers.Dense(units=1, activation = 'linear', )

在这里，'linear’激活函数的作用是保持输出与输入之间的线性关系。在神经网络中，每个层的输出通常会通过一个激活函数来进行非线性变换，以提供网络学习非线性关系的能力。然而，当我们希望保持线性关系时，可以选择使用’linear’激活函数，它实际上仅仅是一个恒等函数，不会对输入进行任何改变。
在这种情况下，Dense层实际上只是执行矩阵相乘和偏置加法，没有经过任何非线性变换，因此输出与输入之间的关系仍然是线性的。这在某些回归任务或特定的网络架构中可能是有用的。

我们来看看权重。

linear_layer.get_weights()

没有权重，因为权重尚未实例化。
让我们在X_train的一个例子上试试这个模型。
这将触发权重的实例化。
注意，图层的输入必须是二维的，所以我们将重塑它。

a1 = linear_layer(X_train[0].reshape(1,1))
print(a1)

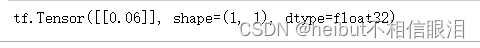
结果是一个形状为（1,1）或一个条目的张量（数组的另一个名称）。现在让我们来看看权重和偏差。这些权重被随机初始化为较小的数字，并且偏置默认被初始化为零。

w, b= linear_layer.get_weights()
print(f"w = {w}, b={b}")

具有单个输入特征的线性回归模型（1）将具有单个权重和偏差。这与我们上面1层的尺寸相匹配。
权重被初始化为随机值，所以让我们将它们设置为一些已知值。

set_w = np.array([[200]])
set_b = np.array([100])# set_weights takes a list of numpy arrays
linear_layer.set_weights([set_w, set_b])
print(linear_layer.get_weights())

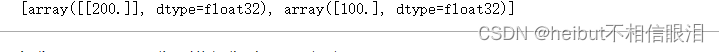
让我们将方程(1)与层输出进行比较。

a1 = linear_layer(X_train[0].reshape(1,1))
print(a1)
alin = np.dot(set_w,X_train[0].reshape(1,1)) + set_b
print(alin)

可以看出无论是用参数设置好的模型计算还是用点积运算得到的结果是一样的。
它们产生相同的值!现在，我们可以使用我们的线性层对我们的训练数据进行预测。

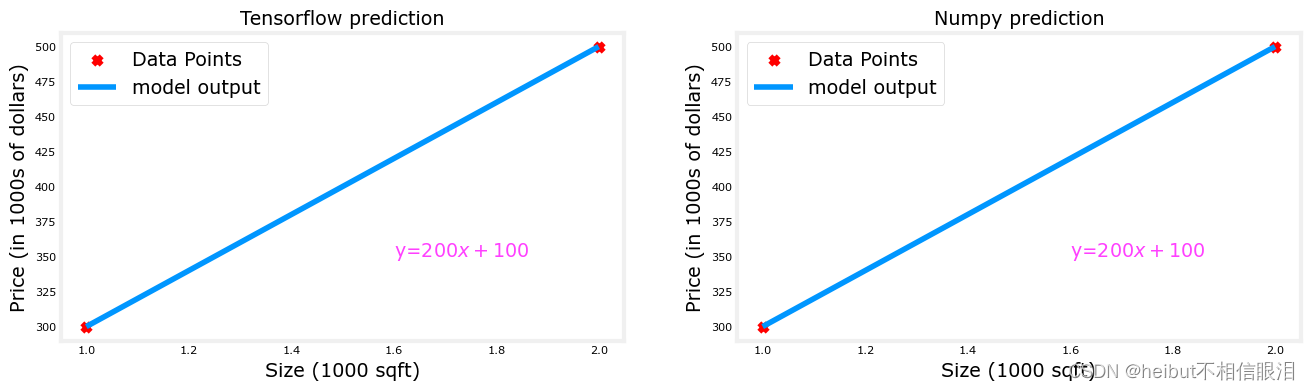
prediction_tf = linear_layer(X_train)
prediction_np = np.dot( X_train, set_w) + set_b

plt_linear(X_train, Y_train, prediction_tf, prediction_np)

Sigmoid激活的神经元

具有Sigmoid激活的神经元/单元实现的功能与课程1中的逻辑回归相同：

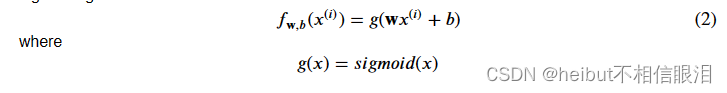
让我们设置𝑤和𝑏并检查模型。
数据集
我们将使用课程1中的一个例子，逻辑回归。

X_train = np.array([0., 1, 2, 3, 4, 5], dtype=np.float32).reshape(-1,1)  # 2-D Matrix
Y_train = np.array([0,  0, 0, 1, 1, 1], dtype=np.float32).reshape(-1,1)  # 2-D Matrix

pos = Y_train == 1
neg = Y_train == 0
X_train[pos]

pos = Y_train == 1
neg = Y_train == 0fig,ax = plt.subplots(1,1,figsize=(4,3))
ax.scatter(X_train[pos], Y_train[pos], marker='x', s=80, c = 'red', label="y=1")
ax.scatter(X_train[neg], Y_train[neg], marker='o', s=100, label="y=0", facecolors='none', edgecolors=dlc["dlblue"],lw=3)ax.set_ylim(-0.08,1.1)
ax.set_ylabel('y', fontsize=12)
ax.set_xlabel('x', fontsize=12)
ax.set_title('one variable plot')
ax.legend(fontsize=12)
plt.show()

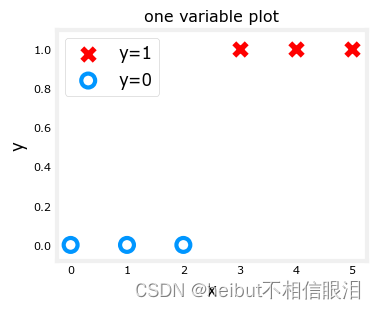
逻辑神经元
我们可以通过添加Sigmoid激活来实现“逻辑神经元”。神经元的功能然后由上面的（2）描述。
本节将创建一个Tensorflow模型，该模型包含我们的逻辑层，以演示创建模型的替代方法。Tensorflow最常用于创建多层模型。序列模型是构建这些模型的一种方便方法。

model = Sequential([tf.keras.layers.Dense(1, input_dim=1,  activation = 'sigmoid', name='L1')]
)

model.summary（）显示模型中的层和参数数量。该模型中只有一个层，而该层只有一个单元。该单元具有两个参数，𝑤和𝑏

model.summary()

logistic_layer = model.get_layer('L1')
w,b = logistic_layer.get_weights()
print(w,b)
print(w.shape,b.shape)

让我们将权重和偏差设置为一些已知值。

set_w = np.array([[2]])
set_b = np.array([-4.5])
# set_weights takes a list of numpy arrays
logistic_layer.set_weights([set_w, set_b])
print(logistic_layer.get_weights())

让我们将等式（2）与层输出进行比较。

a1 = model.predict(X_train[0].reshape(1,1))
print(a1)
alog = sigmoidnp(np.dot(set_w,X_train[0].reshape(1,1)) + set_b)
print(alog)

它们产生了相同的值！现在，我们可以使用我们的逻辑层和NumPy模型对我们的训练数据进行预测。

以下代码是将训练数据 X_train 和标签 Y_train 以及模型的决策边界可视化出来

plt_logistic(X_train, Y_train, model, set_w, set_b, pos, neg)

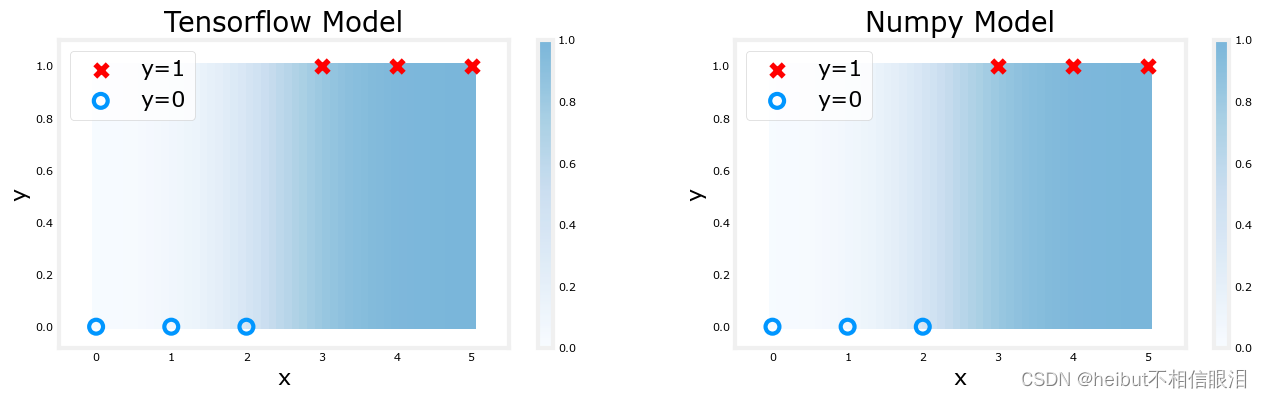
上面的阴影反映了从0到1变化的sigmoid的输出。

祝贺

你建立了一个非常简单的神经网络，并探索了神经元与课程1中的线性和逻辑回归的相似之处。