目录
- 一. 决策树(Decision Tree)
- 1. 决策树的构建
- 1.1 信息熵(Entropy)
- 1.1.1 信息量&信息熵 定义
- 1.1.2 高信息熵&低信息熵 定义
- 1.1.3 信息熵 公式
- 1.2 信息增益(Information Gain)
- 1.2.1 信息增益的计算
- 1.2.2 小节
- 2. 小节
- 2.1 算法分类
- 2.2 决策树算法分割选择
- 2.3 决策树算法的停止条件
- 2.4 决策树算法的评估
本篇我们来开始新的话题——决策树
在正式开始讲解之前,我们先来看一个数据集:
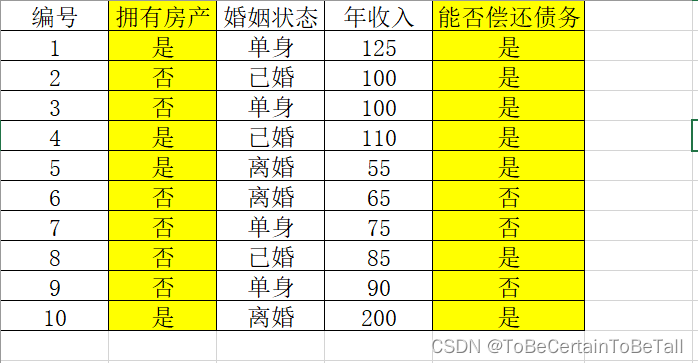
上图展示了银行用于决定是否放贷的数据集。银行通过分析用户特征,预测债务偿还能力,从而决定是否放贷;
针对上面的数据,我们先给出一个决策树的模型:
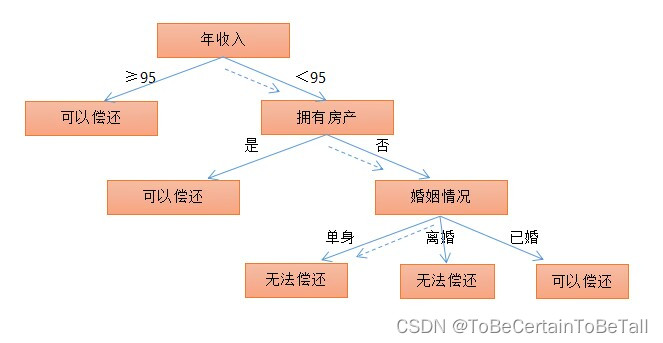
有了这个模型后,当有新数据进入时,我们可以通过数据特征来预测用户是否有能力偿还债务
那么,我们的问题是,怎么构建上图模型?
一. 决策树(Decision Tree)
1. 决策树的构建
对于决策树的构建,我们的主要问题是:
- 首先用哪个特征进行判断呢,即:树的根节点应该是哪个特征?
- 第二层的节点又应该怎样确定呢?
对于节点选择问题,很明显,我们希望最有效(区分度最大)的特征作为根节点,用同样的思路,不断判断区分度最大的特征,从而依次得到下层的节点;如此反复,我们就会得到一个有效的决策树
那么,我们怎样衡量一个划分的“有效性”呢?
1.1 信息熵(Entropy)
1.1.1 信息量&信息熵 定义
- 信息量:如果一个事件发生的概率越大, 那么该事件所蕴含的信息量越少
比如:“地球的自转与公转” ,因为是确定事件,所以不携带任何信息量 - 信息熵:一个系统越是有序,信息熵就越低;一个系统越是混乱,信息熵就越高
人话版:信息熵是一个系统的有序程度的度量
信息熵用来描述系统信息量的不确定度
这里我们举一个例子:
A={1,1,1,1,1,1,2,2,2,2}
B={1,2,3,4,5,6,7,8,9,10}A集合中元素单一化,即信息熵低(越确定,信息熵越低)
B集合中元素多样化,即信息熵高(越不确定,信息熵越高)
1.1.2 高信息熵&低信息熵 定义
-
High Entropy(高信息熵):随机变量X是均匀分布的,各种取值情况是等概率出现的
-
Low Entropy(低信息熵):随机变量X的各种取值不是等概率出现的
对于高信息熵与低信息熵,我们讨论的前提是:1. 都有ABCD四种情况2. ABCD等概率时,信息熵高
如下图:
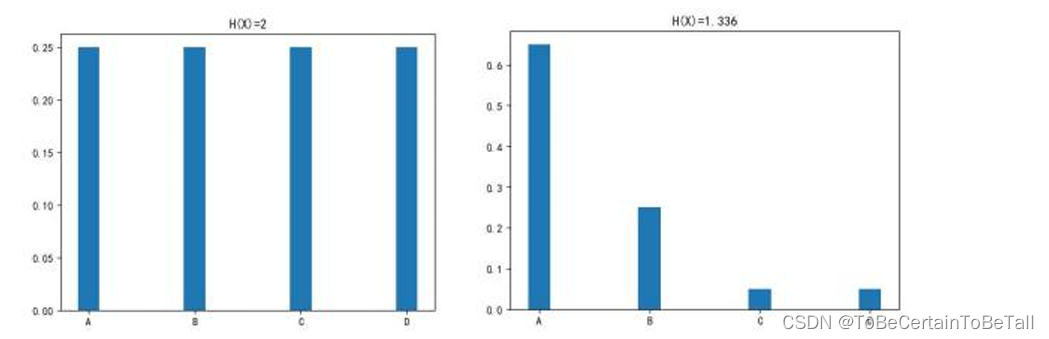
1.1.3 信息熵 公式
H ( X ) = − ∑ i = 1 m p i log 2 ( p i ) H(X)=-\sum_{i=1}^{m}p_{i} \log_{2}({p_{i}}) H(X)=−i=1∑mpilog2(pi)
公式解释:
参数:
p i p_{i} pi表示第i个元素出现的概率
H ( X ) H(X) H(X)信息熵的大小:
- 与m的个数有关
- 与概率p是否平均有关
解释第一条:m越多,则系统越混乱,熵越大
解释第二条:p越平均,信息熵越大
例子:
存在一组数据:0.1,0.1,0.1,0.7,0.7,0.7
第一种分法:(0.1,0.1,0.1)、(0.7,0.7,0.7)
第二种分法:
(0.1,0.1,0.7)、(0.7,0.7,0.1)
最直接的分法为第一种,该分法信息熵为0
1.2 信息增益(Information Gain)
在了解过熵的概念后,我们就可以计算第一次划分得到的信息增益
- 信息增益:用划分之前系统的“熵”减去划分之后系统的“熵”,就是这次划分所获得的“信息增益”
一次划分所获得的“信息增益”越大,则该划分就越有效
1.2.1 信息增益的计算
简单来说,信息增益就是计算增益的加权和
针对开篇给出的数据集,我们对树的构建方式给出具体计算解释:
系统未划分时:
系统的信息熵(偿还能力值:7是,3否)
− 3 10 log 2 3 10 − 7 10 log 2 7 10 = 0.88 -\frac{3}{10} \log_{2}{\frac{3}{10} } -\frac{7}{10} \log_{2}{\frac{7}{10} }=0.88 −103log2103−107log2107=0.88
系统划分时:
-
按照拥有房产情况划分
− 0 4 log 2 0 4 − 4 4 log 2 4 4 = 0.0 -\frac{0}{4} \log_{2}{\frac{0}{4} } -\frac{4}{4} \log_{2}{\frac{4}{4} }=0.0 −40log240−44log244=0.0
− 3 6 log 2 3 6 − 3 6 log 2 3 6 = 1.0 -\frac{3}{6} \log_{2}{\frac{3}{6} } -\frac{3}{6} \log_{2}{\frac{3}{6} }=1.0 −63log263−63log263=1.0
若按照该特征进行划分,信息增益为:
g a i n = 0.88 − 4 10 ∗ 0.0 − 6 10 ∗ 1.0 = 0.28 gain = 0.88-{\frac{4}{10}}*0.0-{\frac{6}{10} }*1.0=0.28 gain=0.88−104∗0.0−106∗1.0=0.28 -
按照婚姻状态划分
− 2 4 log 2 2 4 − 2 4 log 2 2 4 = 1.0 -\frac{2}{4} \log_{2}{\frac{2}{4} } -\frac{2}{4} \log_{2}{\frac{2}{4} }=1.0 −42log242−42log242=1.0
− 0 3 log 2 0 3 − 3 3 log 2 3 3 = 0.0 -\frac{0}{3} \log_{2}{\frac{0}{3} } -\frac{3}{3} \log_{2}{\frac{3}{3} }=0.0 −30log230−33log233=0.0
− 1 3 log 2 1 3 − 2 3 log 2 2 3 = 0.918 -\frac{1}{3} \log_{2}{\frac{1}{3} } -\frac{2}{3} \log_{2}{\frac{2}{3} }=0.918 −31log231−32log232=0.918
若按照该特征进行划分,信息增益为:
g a i n = 0.88 − 4 10 ∗ 1.0 − 3 10 ∗ 0.0 − 3 10 ∗ 0.918 = 0.21 gain =0.88-{\frac{4}{10}}*1.0-{\frac{3}{10} }*0.0-{\frac{3}{10}}*0.918=0.21 gain=0.88−104∗1.0−103∗0.0−103∗0.918=0.21 -
按照年收入划分
针对连续值,我们希望划分可以尽可能的降低系统混乱程度,具体可能出现的分法如下:
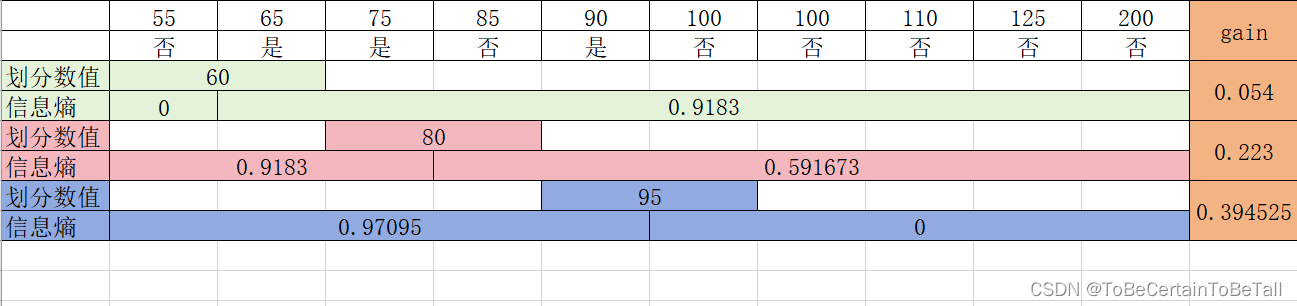
思考:为什么划分数值直接跳过了70?
上面,为了得到符合目标的树,我们分别计算了不同特征作为根节点的信息增益,即
g a i n ( 房产 ) = 0.28 gain(房产) = 0.28 gain(房产)=0.28
g a i n ( 婚姻 ) = 0.21 gain(婚姻)=0.21 gain(婚姻)=0.21
g a i n ( 收入 ) = 0.39 gain(收入)=0.39 gain(收入)=0.39
因此,选择信息增益最大的收入=95作为我们第一次划分划分条件
那么,我们就会得到:
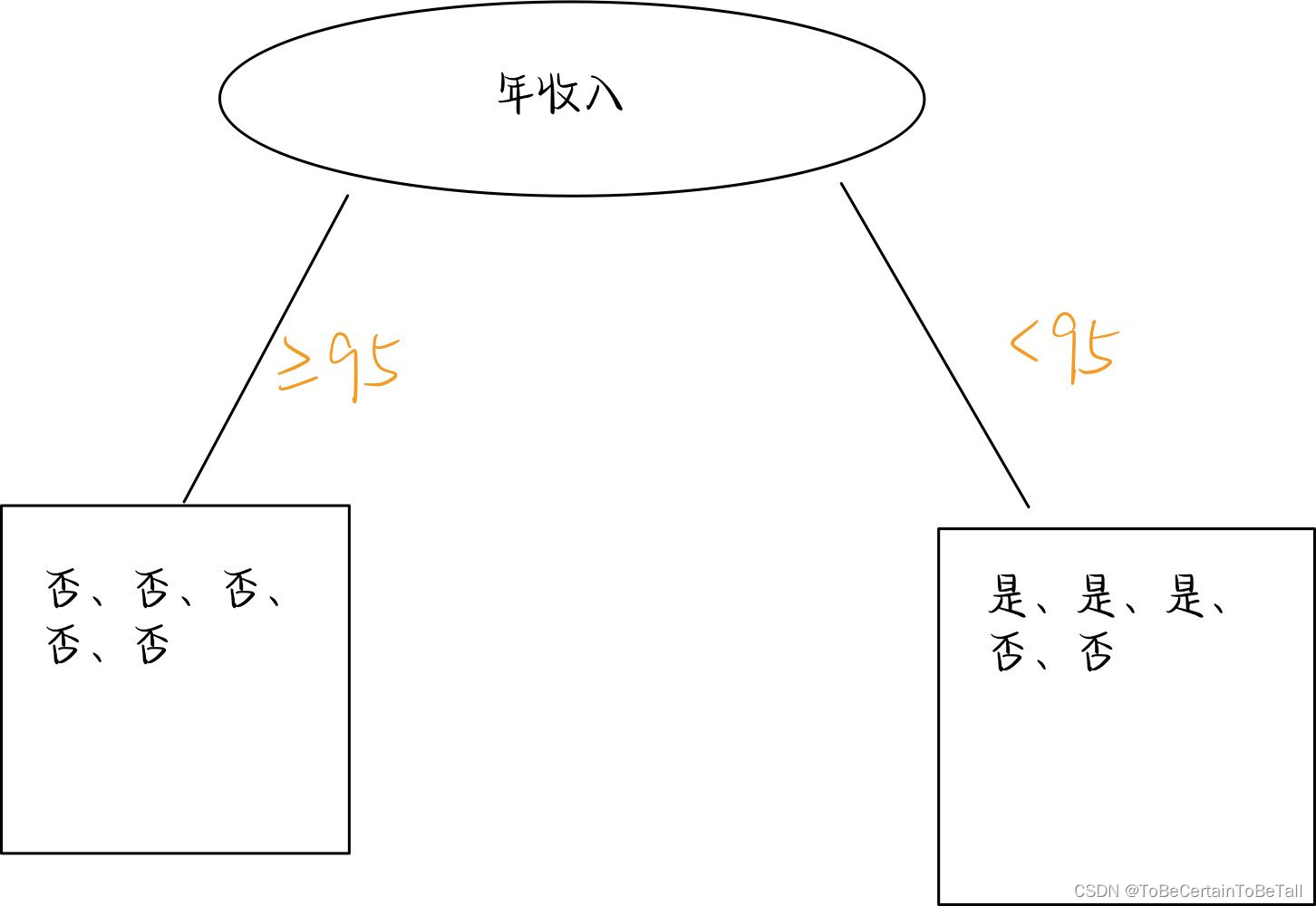
对于第一个节点 ≥ 95 \ge95 ≥95信息熵为0,不需要继续划分
对于第二个节点 < 95 <95 <95信息熵大于0,需要继续划分
即,重复上述计算过程,就可以得到一个完整的决策树
1.2.2 小节
样本集合D中含有k类样本,每个类别所占比例分别为 p k ( k = 1 , 2 , 3 , . . . . ) p_{k}(k=1,2,3,....) pk(k=1,2,3,....),那么集合D的信息熵为:
H ( D ) = − ∑ k = 1 k p k log 2 p k H(D)=-\sum_{k=1}^{k}p_{k}\log_{2}{p_{k}} H(D)=−k=1∑kpklog2pk
假设使用离散特征a对集合D进行划分,且特征a有V个取值,那么信息增益为:
g a i n ( D , a ) = H ( D ) − ∑ v = 1 V p k ∣ D v ∣ ∣ D ∣ H ( D v ) gain(D,a)=H(D)-\sum_{v=1}^{V}p_{k}\frac{\left | D_{v} \right | }{|D|} H(D^{v}) gain(D,a)=H(D)−v=1∑Vpk∣D∣∣Dv∣H(Dv)
2. 小节
决策树算法是一种“贪心”算法策略,只考虑当前,未见得是全局最优,不能进行回溯操作(吃葡萄永远只吃最好的)
决策树是在已知各种情况发生概率的基础上,通过构建决策树来进行分析的一种方式;决策树:一种树形结构每个内部节点表示一个属性的测试每个分支表示一个测试输出每个叶节点代表一种预测类别直观应用概率分析的图解法

2.1 算法分类
决策树是一种常用的有监督算法;从根节点开始,测试待分类项中对应的特征属性,并按照值选择输出分支,直到叶子节点:
-
将叶子节点存放的类别作为决策结果(分类树)
-
将叶子节点存放的值作为决策结果(回归树)
分类树作用:分类标签值回归树作用:预测连续值
2.2 决策树算法分割选择
根据特征属性的类型不同,在构建决策树的时候,采用不同的方式:
属性是离散值时,在不要求生成二叉决策树的前提下,一个属性就是一个分支属性是离散值时,在要求生成二叉决策树的前提下,分支为“属于此子集”和“不属于此子集”属性是连续值时,可以确定一个值作为分裂点,分别按照大于分裂点和小于分裂点生成两个分支
2.3 决策树算法的停止条件
决策树构建是一个递归的过程,如果不给予停止条件,会一直划分,直至叶子节点熵为0;这里我们给出三种常用的停止方式:
1. 当每个叶子节点只有一种类型时,停止构建;即熵为0 ,节点非常纯(会导致过拟合,一般不用)2. 给定树深度值,同时限制叶子节点样本数量小于某个阈值时,停止构建;此时对于不纯的节点,采用最大概率类别作为对应类型3. 限制分裂前后叶子节点中特征数目
2.4 决策树算法的评估
对于分类树:
1. 采用混淆矩阵,即计算准确率,召回率,精确率...2. 采用叶子节点的不纯度总和来评估效果,在确定树深和叶子节点个数的前提下,C(T)越小越好
C ( T ) = − ∑ t = 1 l e a f ∣ D t ∣ D H ( t ) C(T) = -\sum_{t=1}^{leaf} \frac{|D^{t}|}{D}H(t) C(T)=−t=1∑leafD∣Dt∣H(t)
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!



)
/2-4字母(声母)/三杂等品类域名)


 22.1.6 - 多云负载均衡平台)


)


 反馈用于拥塞控制)





