接雨水
- 方法一
- 思路
- 测试代码
- 复杂度
- 测试结果
- 方法二
- 思路
- 测试代码
- 复杂度
- 测试结果
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例1:
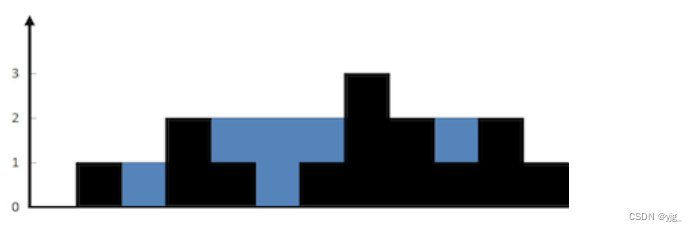
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,
在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
方法一
思路
我们需要维护一个到当前的前缀最大数组(当前元素的前缀最大的数字),和一个到当前的后缀最大数组(当前元素的后缀最大的数字)。
当我们遍历到当前元素的时候,选出前缀和后缀二者中小的那个减去高度即可,得到当前元素的接住的雨水量.

比如相对于这个 height = [0,1,0,2,1,0,1,3,2,1,2,1]高度图,
前缀最大数组是 :pre_max:[0,1,1,2,2,2,2,3,3,3,3,3];
后缀最大数组是: sub_max:[3,3,3,3,3,3,3,3,2,2,2,1];
把遍历到的每一个元素当成一个宽度为1的水桶,他的高就是与其索引一样的前缀最大数组和后缀最大数组中的最小的一个。
测试代码
class Solution{public int trap(int[] height) {int ans=0;int n=height.length;//数组前缀最大值int pre_max[]=new int[n];pre_max[0]=height[0];//后缀最大值数组int sub_max[]=new int[n];sub_max[n-1]=height[n-1];for (int i = 1; i <n; i++) {pre_max[i]=Math.max(height[i],pre_max[i-1]);}for (int i = n-2; i >=0; i--) {sub_max[i]=Math.max(height[i],sub_max[i+1]);}for (int i = 0; i <n; i++) {ans+=Math.min(pre_max[i],sub_max[i])-height[i];}return ans;}
}
复杂度
时间复杂度是:O(n),n,是数组的长度,因为只有三个单层for循环。
空间复杂度是:O(n),创建了两个为长度为n的数组。
测试结果

方法二
思路
我们可以定义两个变量,来维护相对于当前元素的前缀最大值,和后缀最大值。
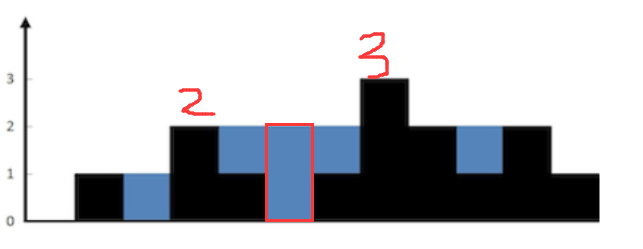
比如这个时候,当我们遍历到红色的框框时候,前缀最大值是2,后缀最大值是3,那么它形成的宽为1木桶,水桶高选择的是前缀,和,后缀小的那个(因为水桶的高度只能选择较小的不,选择大的会溢出去),然后减去高就可以得到当前元素的接雨水的量。
测试代码
class Solution {public int trap(int[] height) {//答案和int ans=0;//前缀最大值int pre_max=0;//后缀最大值int sub_max=0;int i=0,j=height.length-1;while (i<j){//更新前缀最大值pre_max=Math.max(pre_max,height[i]);//更新后缀最大值sub_max=Math.max(sub_max,height[j]);if (pre_max<sub_max){//前缀较小,更新答案ans+=pre_max-height[i];i++;}else {//后缀较小或者等于情况,更新答案ans+=sub_max-height[j];j--;}}return ans;}
}
复杂度
时间复杂度是:O(n)
空间复杂度是:O(1)
测试结果


![[JAVAee]线程安全](http://pic.xiahunao.cn/[JAVAee]线程安全)










)
vue项目中引入外部字体)

)


