注意:本文引用自专业人工智能社区Venus AI
更多AI知识请参考原站 ([www.aideeplearning.cn])
t-SNE是一种用于探索高维数据结构的非线性降维技术。它特别适用于高维数据的可视化,因为它能够在低维空间中保留原始高维数据的局部结构。由于这个特性,t-SNE在机器学习和数据分析领域越来越受到重视。
1 算法解读:
t-SNE的核心思想是在高维空间中为数据点之间定义一种概率分布,表示点与点之间的相似性,然后在低维空间中创建一个相似的概率分布。通过最小化这两个分布之间的差异(使用KL散度),算法将高维数据映射到低维空间,以便我们可以可视化。
2 步骤和细节:
Step 1. 计算高维空间中的相似度
我们使用高斯分布(正态分布)来计算点之间的相似性。高斯分布是一种常见的概率分布,其形状呈钟型,由均值和方差(标准差的平方)决定。高斯分布有一个很好的性质:它的形状由均值(中心点)和方差(分布的宽度)决定。当我们围绕一个数据点 x 画一个高斯分布时,这个分布会给予附近的点较高的概率值,而离得远的点则会有较低的概率值。这与我们直觉上对“相似性”的理解相一致:靠近的点更相似,远离的点不相似。
对于每个数据点,我们计算所有其他点
与其的条件概率
。这个概率反映了点
是 点
的近邻的可能性。计算公式为:
这里,分子部分计算了和
之间的欧氏距离的平方(即
),然后通过高斯分布转换成概率。分母部分是一个归一化因子,确保所有
的和为1。
是高斯分布的方差,决定了近邻的范围。不同的点可能有不同的密度,因此
对于每个 点
可能是不同的,需要通过一种叫做“困惑度”的量来确定。
最后,为了得到一个对称的相似度矩阵,我们取和
的平均值得到 pij :
这样,我们就得到了一个对称的相似度矩阵,其中的每个元素都反映了数据点
和
在高维空间中的相似性。
通过这一步,我们成功地量化了高维空间中数据点之间的相似性,为后续的低维空间嵌入奠 定了基础。
Step 2. 初始化低维空间的点
这一步可以是随机初始化,只需保证初始化点的数量和原数据相同,维度更低即可。
Step 3. 计算低维空间的点的相似度
在t-SNE算法中,高维空间的相似度是通过高斯(正态)分布计算的,而低维空间的相似度是通过t分布(具体来说是自由度为1的t分布,也叫做柯西分布)计算的。这种设计的目的是为了解决“拥挤问题”。
当我们将高维空间中的数据点降维到低维空间时,数据点之间的距离会发生变化。特别是在低维空间中,点与点之间可用的空间更少,容易出现拥挤的情况。如果直接使用高斯分布来计算低维空间的相似度,那么低维空间中远离的点之间的相似度可能会被过高地估计,导致降维结果的可视化效果不佳。
t分布(自由度为1)有一个重要的特性:它的尾部比高斯分布更“厚”(heavy-tailed)。这意味着,在低维空间中,即使两个点距离较远,它们之间的相似度(通过t分布计算)也不会迅速减小到0。这有助于缓解拥挤问题,因为低维空间中远离的点之间的相似度会被较低地估计。对t分布不了解的同学详见数学专栏的博文或视频。
在低维空间中,我们计算点 和
之间的相似度
如下:
这个公式来源于自由度为 1 的t分布。分子部分计算了 和
之间的欧氏距离的平方,并转换成了概率。分母部分是一个归一化因子,确保所有的
之和为1。
通过这种方式,我们得到了低维空间中点之间的相似度矩阵 {} 。接下来,t-SNE算法会试图使高维空间的相似度矩阵 {
} 和低维空间的相似度矩阵 {
} 尽可能地一致,从而得到合适的低维空间表示。
Step 4. 优化低维空间的点的位置
– 通过最小化 Kullback-Leibler 散度 (KL散度) 来优化低维空间中的点的位置。KL散度用于 衡量高维空间和低维空间中的相似度分布之间的差异。
– 使用梯度下降方法来最小化 KL散度,更新低维空间中的点的位置。
在梯度下降的计算中,输入是低维空间中每个点的坐标 {} 。这些坐标是我们要优化的参数。输出是低维空间中点与点之间的相似度 {
} 。这些相似度是由当前的低维坐标 {
} 计 算出来的。标签是高维空间中点与点之间的相似度 {
} 。这些相似度是已知的,因为它们是由原始 高维数据计算得出的。
我们的目标是通过调整低维空间中的点的坐标{ } (即输入),使得由这些坐标计算出的相 似度 {
} (即输出)尽可能接近已知的高维空间的相似度 {
} (即标签)。
为了实现这个目标,我们计算损失函数(即 KL 散度)相对于每个低维坐标的梯度,并使用这 个梯度来更新低维坐标。这个过程会重复进行,直到达到预定的迭代次数,或者低维坐标的 变化小于某个阈值。
3 举例:
我们可以考虑一个更复杂的例子。假设我们有四个四维的数据点,我们想将它们降维到二维空间:
3.1 计算高维空间中的相似度
计算两点间的欧氏距离的平方:
计算条件概率
由于 σ=1 ,我们有:
类似地,我们可以计算其他的 。
对称化
我们得到对称的相似度矩阵 P ,其形式为:
3.2 计算低维空间中的相似度
我们随机初始化低维空间中的点,例如:
计算低维空间中的相似度
计算低维空间中两点间的距离:
计算低维空间中的相似度:
类似地,我们可以计算其他的 ,然后对称化得到矩阵 Q
优化低维空间的点位置
我们使用梯度下降来优化低维空间中的点的位置。其中,
– 输入:这里的输入是低维空间中的点的坐标(初始通常是随机的),我们通过梯度下降来更 新这些坐标,使得低维空间中的相似度矩阵 Q 接近高维空间的相似度矩阵 P 。
– 输出: 经过优化后,低维空间中的点的坐标就是我们的输出。
– 标签: 在这个优化问题中,我们可以将高维空间中的点的相似度 P 视作是“标签”,因为我们 的目标是使低维空间中的点的相似度 Q 尽可能地接近 P 。
在这个意义上,我们是以低维空间的相似度为输入,以高维空间的相似度为标签,通过梯度下降来调整低维空间中的点的坐标,使得两者尽可能一致。
4. 代码实现
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# 定义高维数据点
X = np.array([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12],[13, 14, 15, 16]
])
# 初始化 t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=3)
# 进行 t-SNE 降维
X_tsne = tsne.fit_transform(X)
# 可视化结果
plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
for i, txt in enumerate(['Point 1', 'Point 2', 'Point 3', 'Point 4']):plt.annotate(txt, (X_tsne[i, 0], X_tsne[i, 1]))
plt.title('t-SNE Visualization')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()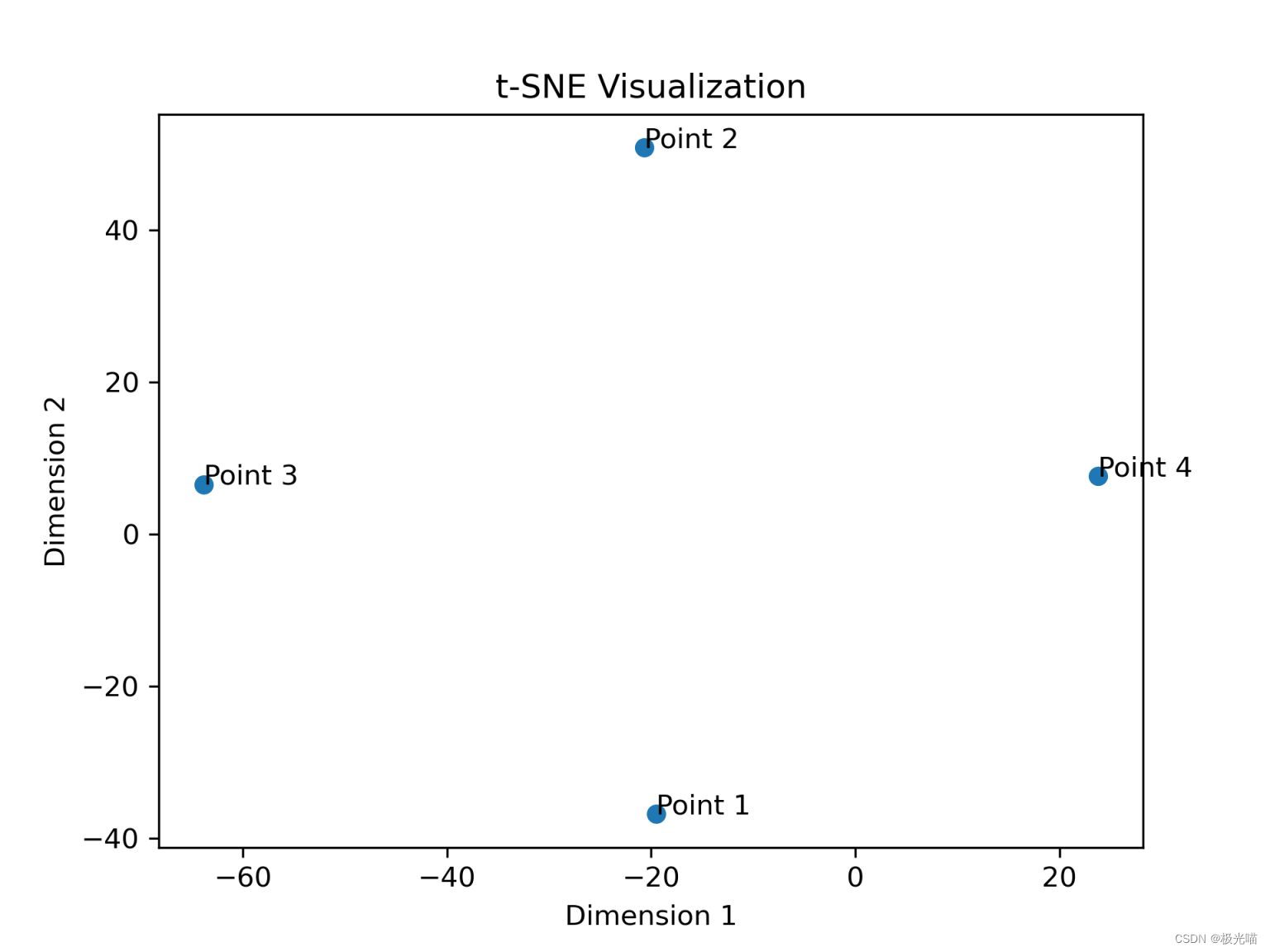
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.cm as cm
# 生成一个三维数据集
np.random.seed(0)
X_3D = np.random.rand(50, 3)
# 创建一个颜色映射
colors = cm.rainbow(np.linspace(0, 1, len(X_3D)))
# 可视化三维数据
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(121, projection='3d')
ax.scatter(X_3D[:, 0], X_3D[:, 1], X_3D[:, 2], c=colors, marker='o')
ax.set_title('Original 3D Data')
# 使用t-SNE降维到2维
tsne = TSNE(n_components=2, random_state=42)
X_2D = tsne.fit_transform(X_3D)
# 可视化降维后的2D数据
ax2 = fig.add_subplot(122)
ax2.scatter(X_2D[:, 0], X_2D[:, 1], c=colors, marker='o')
ax2.set_title('2D Data after t-SNE')
plt.tight_layout()
plt.show()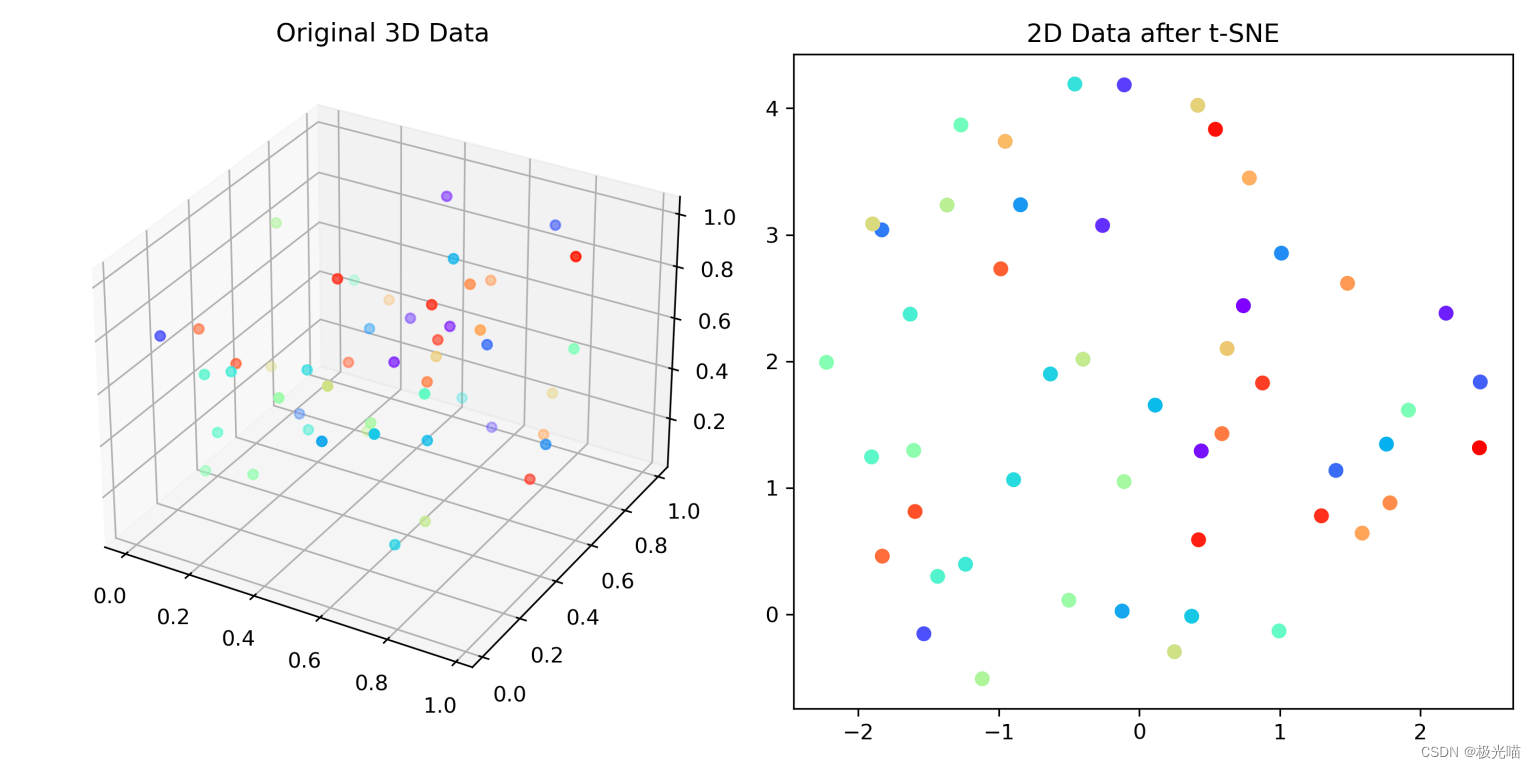
算法评价:
优点
- 保持局部结构:t-SNE 优秀于保持高维数据中的局部结构到低维空间,这意味着在原始空间中相互靠近的点在低维空间中也会靠近。
- 可视化效果佳:t-SNE 算法通常能够产生较好的可视化效果,尤其是对于高维数据,如图像、文本等。
- 对拥挤问题的处理:t-SNE 采用了 t 分布来计算低维空间中的相似度,这有助于缓解拥挤问题(即在低维空间中相互靠近的点过于拥挤)。
- 鲁棒性:t-SNE 对高维空间中的异常点较为鲁棒,能够在某种程度上减小它们对降维结果的影响。
缺点
- 计算复杂度高:t-SNE 算法的计算复杂度较高,特别是当处理大规模数据集时,可能需要较长的计算时间。
- 随机性:t-SNE 的结果受到初始点的随机选择的影响,不同的运行可能会产生不同的结果。
- 超参数敏感:t-SNE 算法有一些超参数,如困惑度(perplexity),需要手动设置。这些参数的选择会影响算法的性能,但很难给出一个通用的最优设置。
- 无法保持全局结构:t-SNE 主要侧重于保持局部结构,但这可能会以损害全局结构为代价,例如可能会将远离的群组拉得过近。
- 不适用于新数据点:t-SNE 没有提供直接的方式来嵌入新的数据点,如果要添加新的数据点,通常需要重新运行整个算法。
- 可能产生拥挤簇:虽然 t-SNE 在一定程度上处理了拥挤问题,但在某些情况下,仍然可能会出现簇的拥挤和重叠。
- 解释性:t-SNE 的可视化结果虽然直观,但由于算法的非线性特性,可能较难解释。例如,低维空间中的距离不一定与高维空间中的距离成正比。
6. 算法变体:
t-SNE 是一种流行的降维算法,已经产生了许多变体,这些变体旨在解决 t-SNE 的某些限制,例如计算效率、稳定性和可扩展性。下面是两个 t-SNE 的变体及其参考文献:
大规模 t-SNE(LargeVis):
论文标题:Visualizing Large-scale and High-dimensional Data
作者:Zhao, J., & Cao, N.
出版年份:2016
链接:arXiv:1602.00370
LargeVis 是为了处理大规模和高维数据而提出的 t-SNE 变体。与 t-SNE 相比,LargeVis 在构建 k-近邻图时采用了一种不同的方法,并使用了负采样技术来优化目标函数,从而显著提高了算法的计算效率。LargeVis 不仅能够快速处理大规模数据集,还能够保持良好的可视化效果。
UMAP(Uniform Manifold Approximation and Projection):
论文标题:UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
作者:McInnes, L., Healy, J., & Melville, J.
出版年份:2018
链接:arXiv:1802.03426
UMAP 是一种基于流形学习的降维算法,它可以被视为 t-SNE 的一种变体,但具有更广泛的应用场景。UMAP 在保持局部和全局结构方面表现优秀,计算效率高,且能够适应不同类型的数据和学习任务。UMAP 也适用于新数据点的嵌入,这是传统 t-SNE 不具备的特性。
这两种变体都通过各自的方法改善了 t-SNE 的某些方面,值得在实际应用中尝试和比较。
![[WUSTCTF2020]朴实无华](http://pic.xiahunao.cn/[WUSTCTF2020]朴实无华)






)





)



![[M贪心] lc2789. 合并后数组中的最大元素(贪心+思维)](http://pic.xiahunao.cn/[M贪心] lc2789. 合并后数组中的最大元素(贪心+思维))

