🤔决策树算法

决策树的思想来源可以追溯到古希腊时期，当时的哲学家们就已经开始使用类似于决策树的图形来表示逻辑推理过程。然而，决策树作为一种科学的决策分析工具，其发展主要发生在20世纪。

在20世纪50年代，美国兰德公司的研究人员在研究军事策略时首次提出了决策树的概念。他们使用决策树来分析和比较不同的军事策略，以帮助决策者做出最佳选择。

决策树的基本思想是，通过构建一个树状的图形模型，将决策过程中的各种可能情况和结果以直观的方式展现出来。每一个节点代表一个决策或事件，每一个分支代表一个可能的结果，而树的每一个路径则代表一种可能的决策序列。这种思想的朴素之处在于，它直接模仿了人类在日常生活中做决策的过程。人们在面对一个复杂的问题时，往往会将其分解为一系列的小问题，然后逐个解决。当选择一个餐厅时，可能会考虑菜品的口味、价格区间、餐厅的位置等因素。这些因素可以构成一个决策树，其中每个因素是决策节点，每个选择是方案枝，最终到达叶子节点，即做出决策。

决策树的思想虽然朴素，但它却能够处理非常复杂的决策问题，因此被广泛应用于经济学、管理学、计算机科学等多个领域。

🔎sklearn实现决策树分类

鸢尾花数据绘制图像

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn import tree
import matplotlib.pyplot as plt# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建决策树分类器
clf = DecisionTreeClassifier()# 训练模型
clf.fit(X_train, y_train)# 预测测试集
y_pred = clf.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率：", accuracy)# 绘制决策树图像
fig, ax = plt.subplots(figsize=(12, 12))
tree.plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, ax=ax)
plt.show()

构建决策树包括三个：

• 特征选择：选取有较强分类能力的特征

• 决策树生成

• 决策树剪枝

 🔎ID3 决策树

 ID3 树是基于信息增益构建的决策树，算法的核心在于使用信息增益作为属性选择的标准，即在每个节点选择尚未被用来划分的、具有最高信息增益的属性作为划分标准。通过这种方式，算法递归地构建决策树，直到所有的训练样本都能被完美分类。

• 计算信息熵：首先需要了解信息熵的概念，它衡量的是数据集中的不确定性或混乱程度。信息熵的计算公式为 Entropy = -∑(p(xi) * log2(p(xi)))，其中 p(xi) 是第 i 类样本出现的概率。

• 熵越大，数据的不确定性度越高
• 熵越小，数据的不确定性越低

假如有三个类别，分别占比为：{⅓,⅓,⅓}，信息熵计算结果 1.0986；

若分别占比为：{1/10,2/10,7/10}，信息熵计算结果为 0.8018。

import numpy as np
import matplotlib.pyplot as pltdef entropy(p):return -p*np.log(p)-(1-p)*np.log(1-p)x = np.linspace(0.01,0.99,200)
plt.plot(x,entropy(x))
plt.show()

 

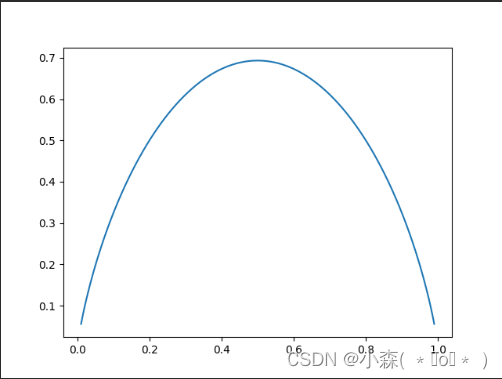
当我们的系统每一个类别是等概率的时候，系统的信息熵最高，直到系统整体百分之百的都到某一类中，此时信息熵就达到了最低值。

条件熵用于衡量以某个特征作为条件，对目标值纯度的提升程度。

💡信息增益

信息增益反映了在一个条件下，信息的不确定性减少了多少。它是通过计算信息熵和条件熵的差值得出的。条件熵是在已知某个条件或属性的情况下，数据集的不确定性。它通常用于衡量在给定某个属性的条件下，目标变量的不确定性。信息增益差值越大，说明该属性对于分类的贡献越大，因此在构建决策树时，我们倾向于选择信息增益大的属性作为节点的划分依据。

🔎C4.5 决策树

C4.5决策树算法是ID3算法的改进版本，它使用信息增益率来选择划分特征。

C4.5算法在构建决策树时采用了与ID3算法相似的自顶向下的贪婪搜索策略，但它在以下几个方面进行了重要的改进和优化：

• 信息增益率：C4.5算法使用信息增益率而非信息增益来选择划分特征。信息增益率是信息增益与分裂信息（split information）的比值，这种方法克服了ID3算法中信息增益倾向于选择取值较多的属性的不足。
• 处理连续属性：C4.5算法能够处理离散型和连续型的属性。对于连续型属性，算法会进行离散化处理，将其转换为可以用于决策树的离散值。
• 剪枝操作：在构造决策树之后，C4.5算法会进行剪枝操作，以减少模型的过拟合风险，提高模型的泛化能力。
• 处理缺失值：C4.5算法能够处理具有缺失属性值的训练数据，这使得算法更加健壮和适用于现实世界的数据。
• 数据：C4.5算法可以处理离散型描述属性，也可以处理连续数值型属性

🔎CART 分类决策树 

CART，全称为Classification and Regression Tree，即分类回归树，是一种非常灵活且功能强大的机器学习算法。它与之前的ID3和C4.5算法不同，CART能够处理连续型数据的分类以及回归任务。CART生成的是二叉树，这意味着在每个非叶节点上只会有两个分支。这样的结构有助于简化模型，提高解释性。CART使用基尼系数作为特征选择的标准。基尼系数衡量的是数据集的不纯度，基尼系数越小，表示数据越纯，即分类越明确。这与信息增益（率）的概念相反，后者是在ID3和C4.5中使用的。

基尼指数值越小（cart），则说明优先选择该特征。假设有一个包含两个类别的数据集，其中类别A有10个样本，类别B有20个样本。我们可以使用以下公式计算基尼指数：

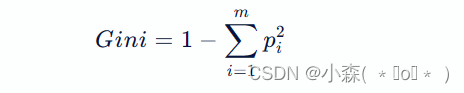
其中，pi​是第i个类别在数据集中出现的概率，m是类别的数量。在这个例子中，m=2 ，因此：Gini=1−(10/30)2−(20/30)2=0.475

这意味着这个数据集的基尼指数为0.475，表示数据集的不纯度较高，基尼指数只适用于二分类问题，对于多分类问题需要使用其他指标，如信息增益、信息增益率等。

🔎Cart分类树原理 

如果目标变量是离散变量，则是classfication Tree分类树。决策树算法对训练集很容易过拟合，导致泛化能力很差，为解决此问题，需要对CART树进行剪枝。CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小，从而能够对未知数据有更准确的预测，也就是说CART使用的是后剪枝法。一般分为两步：先生成决策树，产生所有可能的剪枝后的CART树，然后使用交叉验证来检验各种剪枝的效果，最后选择泛化能力好的剪枝策略。

 

💎 决策树算法sklearn总结

 在sklearn中，决策树算法主要通过DecisionTreeClassifier类实现。DecisionTreeClassifier类的构造方法接受多个参数，用于控制决策树的构建过程和行为。

• criterion：用于特征选择的准则，可选"gini"（基尼系数）或"entropy"（信息增益）。
• splitter：用于节点划分的策略，可选"best"（最优划分）或"random"（随机划分）。
• max_depth：决策树的最大深度，用于防止过拟合。
• min_samples_split：内部节点再划分所需最小样本数。
• min_samples_leaf：叶节点所需的最小样本数。
• class_weight：类别权重，用于处理不平衡数据集。

训练方法：使用fit方法来训练决策树模型，传入训练数据和对应的标签。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier# 加载数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=42)# 创建决策树分类器实例
clf = DecisionTreeClassifier(criterion="gini", max_depth=4)# 训练模型
clf.fit(X_train, y_train)

预测方法：使用predict方法进行预测，输入待预测的数据，输出预测结果。

y_pred = clf.predict(X_test)

评估方法：可以使用score方法来评估模型的准确性。

# 计算准确率
accuracy = clf.score(X_test, y_test)

sklearn中的决策树算法提供了一个灵活且易于使用的机器学习模型，适用于各种分类问题。通过调整不同的参数和选择合适的特征选择准则，可以有效地控制决策树的行为和性能。