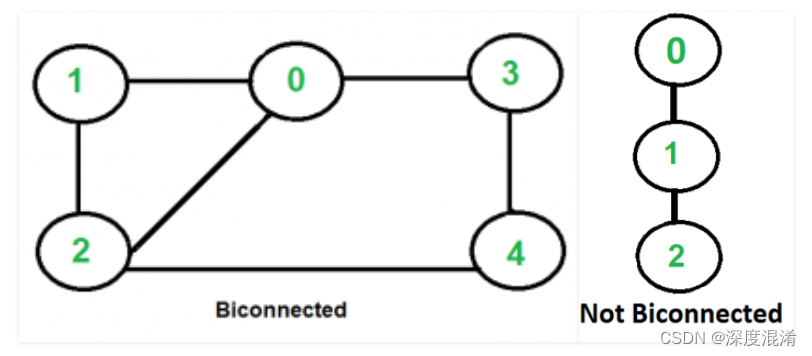
1 双连通图(Biconnected Components of Graph)
如果任意两个顶点之间有两条顶点不相交的路径,则无向图称为双连通图。在双连通图中,有一个通过任意两个顶点的简单循环。
按照约定,由边连接的两个节点构成双连通图,但这并不验证上述属性。对于具有两个以上顶点的图,必须存在上述属性才能进行双连接。或者换句话说:
如果满足以下条件,则称图形为双连通:
1) 它是连接的,即可以通过一条简单的路径从其他每个顶点到达每个顶点。
2) 即使移除任何顶点,图形仍保持连接。
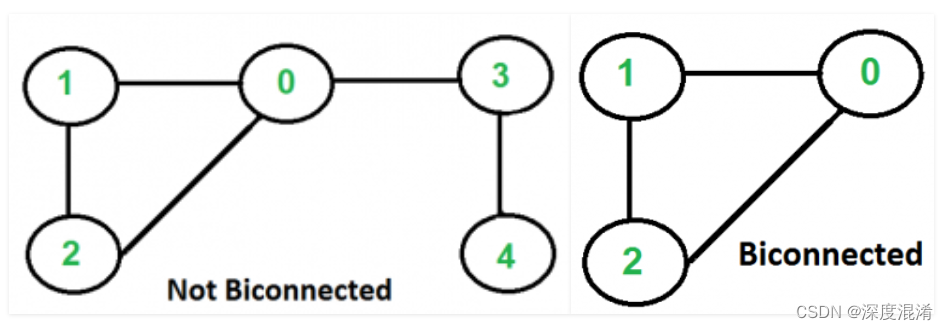
如果一个连通图是连通的并且没有任何连接点,那么它就是双连通的。我们主要需要检查图表中的两件事。
1) 图形已连接。
2) 图表中没有连接点。
我们从任何顶点开始进行DFS遍历。在DFS遍历中,我们检查是否有任何连接点。如果我们没有找到任何连接点,那么该图是双连接的。最后,我们需要检查是否所有顶点都可以在DFS中访问。如果所有顶点都不可到达,则图形甚至没有连接。
2 源程序
using System;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public partial class Graph
{
private void Biconnected_Components_Utility(int u, int[] disc, int[] low,ref List<Edge> st, int[] parent)
{
disc[u] = low[u] = ++time;
int children = 0;
foreach (int it in Adjacency[u])
{
int v = it;
if (disc[v] == -1)
{
children++;
parent[v] = u;
st.Add(new Edge(u, v));
Biconnected_Components_Utility(v, disc, low,ref st, pa




管理系统,帅呆了~~)
Token 概念)








)




