普林斯顿算法讲义（一）

原文：普林斯顿大学算法课程

译者：飞龙

协议：CC BY-NC-SA 4.0

1. 基础知识

原文：algs4.cs.princeton.edu/10fundamentals

译者：飞龙

协议：CC BY-NC-SA 4.0

概述。

本书的目标是研究各种重要和有用的算法——解决问题的方法适合计算机实现。算法与数据结构——组织数据的方案密切相关。本章介绍了我们研究算法和数据结构所需的基本工具。

1.1 编程模型介绍了我们的基本编程模型。我们所有的程序都是使用 Java 编程语言的一个小子集以及一些用于输入和输出的自定义库来实现的。
1.2 数据抽象强调数据抽象，我们定义抽象数据类型（ADTs）。我们指定一个应用程序编程接口（API），然后使用 Java 类机制开发一个实现，供客户端代码使用。
1.3 背包、队列和栈考虑了三种基本的 ADT：背包、队列和栈。我们使用调整大小数组和链表描述 API 和实现。
1.4 算法分析描述了我们分析算法性能的方法。我们方法的基础是科学方法：我们提出关于性能的假设，创建数学模型，并进行实验来测试它们。
1.5 案例研究：并查集是一个案例研究，我们考虑解决一个连接性问题的解决方案，该问题使用实现经典并查集ADT 的算法和数据结构。

本章中的 Java 程序。

下面是本章中的 Java 程序列表。点击程序名称以访问 Java 代码；点击参考号以获取简要描述；阅读教材以获取详细讨论。

REF PROGRAM 描述 / JAVADOC
- BinarySearch.java 二分查找
- RandomSeq.java 给定范围内的随机数
- Average.java 一系列数字的平均值
- Cat.java 连接文件
- Knuth.java Knuth 洗牌
- Counter.java 计数器
- StaticSETofInts.java 整数集合
- Allowlist.java 白名单客户端
- Vector.java 欧几里得向量
- Date.java 日期
- Transaction.java 交易
- Point2D.java 点
- RectHV.java 轴对齐矩形
- Interval1D.java 1d 区间
- Interval2D.java 2d 区间
- Accumulator.java 运行平均值和标准差
1.1 ResizingArrayStack.java LIFO 栈（调整大小数组）
1.2 LinkedStack.java 后进先出栈（链表）
- Stack.java 后进先出栈
- ResizingArrayQueue.java 先进先出队列（调整大小数组）
1.3 LinkedQueue.java 先进先出队列（链表）
- Queue.java 先进先出队列
- ResizingArrayBag.java 多重集（调整大小数组）
1.4 LinkedBag.java 多重集（链表）
- Bag.java 多重集
- Stopwatch.java 计时器（墙上时间）
- StopwatchCPU.java 计时器（CPU 时间）
- LinearRegression.java 简单线性回归
- ThreeSum.java 暴力三数求和
- ThreeSumFast.java 更快的三数求和
- DoublingTest.java 倍增测试
- DoublingRatio.java 倍增比率
- QuickFindUF.java 快速查找
- QuickUnionUF.java 快速联合
1.5 WeightedQuickUnionUF.java 加权快速联合
- UF.java 按秩合并并路径减半

REF	PROGRAM	描述 / JAVADOC
-	BinarySearch.java	二分查找
-	RandomSeq.java	给定范围内的随机数
-	Average.java	一系列数字的平均值
-	Cat.java	连接文件
-	Knuth.java	Knuth 洗牌
-	Counter.java	计数器
-	StaticSETofInts.java	整数集合
-	Allowlist.java	白名单客户端
-	Vector.java	欧几里得向量
-	Date.java	日期
-	Transaction.java	交易
-	Point2D.java	点
-	RectHV.java	轴对齐矩形
-	Interval1D.java	1d 区间
-	Interval2D.java	2d 区间
-	Accumulator.java	运行平均值和标准差
1.1	ResizingArrayStack.java	LIFO 栈（调整大小数组）
1.2	LinkedStack.java	后进先出栈（链表）
-	Stack.java	后进先出栈
-	ResizingArrayQueue.java	先进先出队列（调整大小数组）
1.3	LinkedQueue.java	先进先出队列（链表）
-	Queue.java	先进先出队列
-	ResizingArrayBag.java	多重集（调整大小数组）
1.4	LinkedBag.java	多重集（链表）
-	Bag.java	多重集
-	Stopwatch.java	计时器（墙上时间）
-	StopwatchCPU.java	计时器（CPU 时间）
-	LinearRegression.java	简单线性回归
-	ThreeSum.java	暴力三数求和
-	ThreeSumFast.java	更快的三数求和
-	DoublingTest.java	倍增测试
-	DoublingRatio.java	倍增比率
-	QuickFindUF.java	快速查找
-	QuickUnionUF.java	快速联合
1.5	WeightedQuickUnionUF.java	加权快速联合
-	UF.java	按秩合并并路径减半

1.1 编程模型

原文：algs4.cs.princeton.edu/11model

译者：飞龙

协议：CC BY-NC-SA 4.0

本节正在大规模施工中。

我们对算法的研究基于将它们作为用 Java 编程语言编写的程序来实现。我们这样做有几个原因：

我们的程序是算法的简洁、优雅和完整描述。
您可以运行程序来研究算法的属性。
您可以立即将算法应用于应用程序中。

原始数据类型和表达式。

数据类型是一组值和对这些值的一组操作。以下四种原始数据类型是 Java 语言的基础：

整数，带有算术运算（int）
实数，再次带有算术运算（double）
布尔值，值集合为{ true, false }，带有逻辑运算（boolean）
字符，您键入的字母数字字符和符号（char）

一个 Java 程序操作用标识符命名的变量。每个变量与数据类型关联，并存储其中一个可允许的数据类型值。我们使用表达式来应用与每种类型相关的操作。

以下表总结了 Java 的int、double、boolean和char数据类型的值集合和最常见操作。

表达式。 典型表达式为中缀。当一个表达式包含多个运算符时，优先级顺序指定它们应用的顺序：运算符*和/（以及%）的优先级高于（在+和-运算符之前应用）；在逻辑运算符中，!具有最高优先级，其次是&&，然后是||。通常，相同优先级的运算符是左结合（从左到右应用）。您可以使用括号来覆盖这些规则。
类型转换。 如果不会丢失信息，数字会自动提升为更包容的类型。例如，在表达式1 + 2.5中，1被提升为double值1.0，表达式求值为double值3.5。强制转换是将一个类型的值转换为另一个类型的指令。例如(int) 3.7是3。将double转换为int会朝向零截断。
比较。 以下混合类型运算符比较相同类型的两个值并产生一个boolean值：
- 等于（==)
- 不等于（!=)
- 小于（<)
- 小于或等于（<=)
- 大于（>）
- 大于或等于（>=)
其他原始类型。 Java 的int有 32 位表示；Java 的double类型有 64 位表示。Java 还有五种额外的原始数据类型：
- 64 位整数，带有算术运算（long）
- 16 位整数，带有算术运算（short）
- 16 位字符，带有算术运算（char）
- 8 位整数，带有算术运算（byte）
- 32 位单精度实数，带有算术运算（float）

语句。

一个 Java 程序由语句组成，通过创建和操作变量、为它们分配数据类型值以及控制这些操作的执行流程来定义计算。

声明创建指定类型的变量并用标识符命名它们。Java 是一种强类型语言，因为 Java 编译器会检查一致性。变量的作用域是程序中定义它的部分。
赋值将数据类型值（由表达式定义）与变量关联。
初始化声明将声明与赋值结合在一起，以初始化变量的同时声明变量。
隐式赋值。 当我们的目的是相对于当前值修改变量的值时，可以使用以下快捷方式：
- 递增/递减运算符：代码i++是i = i + 1��简写。代码++i相同，只是在递增/递减之后取表达式值，而不是之前。
- 其他复合运算符：代码i /= 2是i = i/2的简写。
条件语句提供了对执行流程的简单改变——根据指定条件在两个块中的一个中执行语句。
循环提供了对执行流程的更深刻改变——只要给定条件为真，就执行块中的语句。我们将循环中的语句称为循环的主体。
中断和继续。 Java 支持在 while 循环中使用的两个额外语句：
- break语句，立即退出循环
- continue语句，立即开始循环的下一次迭代
关于符号。 许多循环遵循这种方案：将索引变量初始化为某个值，然后使用while循环来测试涉及索引变量的循环继续条件，其中while循环中的最后一条语句递增索引变量。您可以使用 Java 的for符号简洁地表示这样的循环。
单语句块。 如果条件或循环中的语句块只有一个语句，则大括号可以省略。

以下表格说明了不同类型的 Java 语句。

数组。

数组存储相同类型的值序列。如果有N个值，我们可以使用符号a[i]来引用i的值，其中i的值从0到N-1。

创建和初始化数组。 在 Java 程序中创建数组涉及三个不同的步骤：
- 声明数组名称和类型。
- 创建数组。
- 初始化数组值。
默认数组初始化。 为了节省代码，我们经常利用 Java 的默认数组初始化约定，并将所有三个步骤合并为一个语句。数值类型的默认初始值为零，boolean类型的默认值为false。
初始化声明。 我们可以在编译时指定初始化值，通过在大括号之间列出逗号分隔的文字值。
使用数组。 一旦创建数组，其大小就固定了。程序可以使用代码a.length引用数组a[]的长度。Java 进行自动边界检查——如果您使用非法索引访问数组，程序将以ArrayIndexOutOfBoundsException终止。
别名。 数组名称指代整个数组——如果我们将一个数组名称分配给另一个数组名称，则两者都指代同一个数组，如下面的代码片段所示。
```
int[] a = new int[N];
...
a[i] = 1234;
...
int[] b = a;
...
b[i] = 5678;   // a[i] is now 5678.
```
这种情况被称为别名，可能导致微妙的错误。
二维数组。 在 Java 中，二维数组是一维数组的数组。二维数组可能是不规则的（其数组的长度可能各不相同），但我们通常使用（对于适当的参数 M 和 N）M×N 的二维数组。要引用二维数组a[][]中第i行第j列的条目，我们使用表示法a[i][j]。

静态方法。

许多编程语言中称静态方法为函数，因为它们可以像数学函数一样运行。每个静态方法是一系列语句，当调用静态方法时，这些语句将依次执行。

定义静态方法。 方法封装了一系列语句定义的计算。方法接受参数（给定数据类型的值）并计算某种数据类型的返回值或引起副作用。每个静态方法由签名和主体组成。
调用静态方法。 对静态方法的调用是其名称，后跟用逗号分隔的括号中指定参数值的表达式。当调用方法时，其参数变量将用调用中相应表达式的值初始化。return语句终止静态方法，将控制返回给调用者。如果静态方法要计算一个值，那么该值必须在return语句中指定。
方法的属性。 Java 方法具有以下特点：
- 参数按值传递。 调用函数时，参数值会被完全评估，并且生成的值会复制到参数变量中。这被称为按值传递。数组（和其他对象）引用也是按值传递的：方法无法更改引用，但可以更改数组中的条目（或对象的值）。
- 方法名可以重载。 类中的方法可以具有相同的名称，只要它们具有不同的签名。这个特性被称为重载。
- 方法具有单个返回值，但可能有多个返回语句。 Java 方法只能提供一个返回值。一旦到达第一个return语句，控制就会返回到调用程序。
- 方法可能具有副作用。 方法可以使用关键字void作为其返回类型，以指示它没有返回值并产生副作用（消耗输入，产生输出，更改数组中的条目，或以其他方式更改系统的状态）。
递归。 递归方法是一种直接或间接调用自身的方法。在开发递归程序时有三个重要的经验法则：
- 递归有一个基本情况。
- 递归调用必须处理在某种意义上更小的子问题，以便递归调用收敛到基本情况。
- 递归调用不应处理重叠的子问题。
基本编程模型。 一组静态方法的库是在 Java 类中定义的一组静态方法。Java 编程的基本模型是通过创建一组静态方法的库来解决特定的计算任务，其中一个方法被命名为main()。
模块化编程。 静态方法库使模块化编程成为可能，其中一个库中的静态方法可以调用其他库中定义的静态方法。这种方法有许多重要的优点。
- 使用合理大小的模块进行工作
- 共享和重用代码，而无需重新实现它
- 替换改进的实现
- 为解决编程问题开发适当的抽象模型
- 本地化调试
单元测试。 Java 编程中的最佳实践是在每个静态方法库中包含一个main()，用于测试库中的方法。
外部库。 我们使用来自三种不同类型的库的静态方法，每种库都需要（略有）不同的代码重用程序。
- java.lang中的标准系统库，包括java.lang.Math，java.lang.Integer和java.lang.Double。这些库在 Java 中始终可用。
- 导入的系统库，如java.util.Arrays。程序开头需要一个import语句来使用这些库。
- 本书中的库。按照这些说明添加 algs4.jar 到您的 Java 类路径。
要从另一个库调用方法，我们在每次调用时在方法名前加上库名：Math.sqrt()，Arrays.sort()，BinarySearch.rank()和StdIn.readInt()。

API。

Java 库。
我们的标准库。
您自己的库。

字符串。

连接。
转换。
自动转换。
命令行参数。

输入和输出。

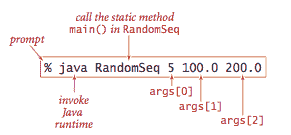
命令和参数。
标准输出。
格式化输出。
标准输入。
重定向和管道。
从文件中输入和输出。
标准绘图。

二分查找。

下面是一个完整的 Java 程序 BinarySearch.java，演示了我们编程模型的许多基本特性。它实现了一种称为二分查找的经典算法，并对其进行了白名单过滤应用的测试。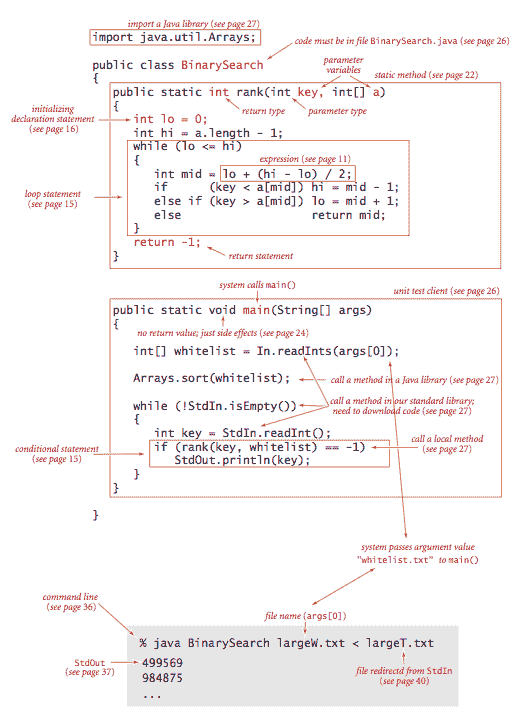二分查找的解剖静态方法rank()接受一个整数键和一个排序的int值数组作为参数，并在数组中返回键的索引，否则返回-1。它通过维护变量lo和hi来完成这个任务，使得如果键在a[lo..hi]中，则进入一个循环，测试间隔中的中间条目（在��引mid处）。如果键等于a[mid]，则返回值为mid；否则，该方法将间隔大小减半，如果键小于a[mid]，则查看左半部分，如果键大于a[mid]，则查看右半部分。当找到键或间隔为空时，该过程终止。有序数组中的二分查找

开发客户端。
白名单。 在测试中，我们使用样本文件 tinyAllowlist.txt，tinyText.txt，largeAllowlist.txt 和 largeText.txt。
性能。

输入和输出库。

这是我们在整本教材以及更多领域中使用的输入和输出库列表。

程序 描述 / JAVADOC
StdIn.java 从标准输入读取数字和文本
StdOut.java 将数字和文本写入标准输出
StdDraw.java 在窗口中绘制几何形状
StdAudio.java 创建、播放和操作声音
StdRandom.java 生成随机数
StdStats.java 计算统计数据
StdArrayIO.java 读取和写入 1D 和 2D 数组
In.java 从文件和 URL 读取数字和文本
Out.java 将数字和文本写入文件
Draw.java 绘制几何形状
DrawListener.java 在 Draw 中支持键盘和鼠标事件
Picture.java 处理数字图像
Stopwatch.java 测量运行时间
BinaryStdIn.java 从标准输入读取位
BinaryStdOut.java 将位写入标准输出
BinaryIn.java 从文件和 URL 读取位
BinaryOut.java 将位写入文件

程序	描述 / JAVADOC
StdIn.java	从标准输入读取数字和文本
StdOut.java	将数字和文本写入标准输出
StdDraw.java	在窗口中绘制几何形状
StdAudio.java	创建、播放和操作声音
StdRandom.java	生成随机数
StdStats.java	计算统计数据
StdArrayIO.java	读取和写入 1D 和 2D 数组
In.java	从文件和 URL 读取数字和文本
Out.java	将数字和文本写入文件
Draw.java	绘制几何形状
DrawListener.java	在 Draw 中支持键盘和鼠标事件
Picture.java	处理数字图像
Stopwatch.java	测量运行时间
BinaryStdIn.java	从标准输入读取位
BinaryStdOut.java	将位写入标准输出
BinaryIn.java	从文件和 URL 读取位
BinaryOut.java	将位写入文件

我们简要描述输入和输出库，并包含一个示例客户端。

标准输入和标准输出。

StdIn.java 和 StdOut.java 是用于从标准输入读取数字和文本并将数字和文本打印到标准输出的库。我们的版本比相应的 Java 版本具有更简单的接口（并提供一些技术改进）。RandomSeq.java 生成给定范围内的随机数。Average.java 从标准输入读取一系列实数，并在标准输出上打印它们的平均值。

% java Average
10.0 5.0 6.0 3.0 7.0 32.0
3.14 6.67 17.71
<Ctrl-d>
Average is 10.05777777777778

In.java 和 Out.java 是支持多个输入和输出流的面向对象版本，包括从文件或 URL 读取和写入文件。

标准绘图。

StdDraw.java 是一个易于使用的库，用于绘制几何形状，如点、线和圆。RightTriangle.java 绘制一个直角三角形和一个外接圆。

Draw.java 是支持在多个窗口中绘图的面向对象版本。

标准音频。

StdAudio.java 是一个易于使用的合成声音库。Tone.java 从命令行读取频率和持续时间，并为给定持续时间的给定频率声音化正弦波。

% java Tone 440.0 3.0

图像处理。

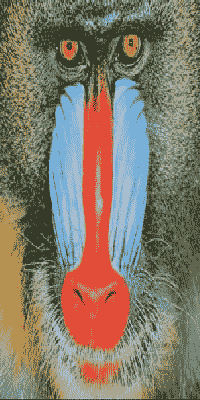
Picture.java 是一个易于使用的图像处理库。Scale.java 接受图片文件的名称和两个整数（宽度 w 和高度 h）作为命令行参数，并将图像缩放到 w-by-h。

| % java Scale mandrill.jpg 298 298 |

298-by-298 |

| % java Scale mandrill.jpg 200 200 |

200-by-400 |

| % java Scale mandrill.jpg 200 400 |

200-by-400 |

问答

Q. 使用一个好的洗牌算法有多重要？

A. 这里有一个有趣的轶事，讲述了当你没有正确执行时会发生什么（尤其是在你的业务是在线扑克时！）。如果你经营一个在线赌场，这里是洗牌一副牌的推荐方法：（i）使用一个密码学安全的伪随机数生成器，（ii）为每张卡分配一个随机的 64 位数字，（iii）根据它们的数字对卡进行排序。

创意问题

二项分布。 估计方法调用binomial1(100, 50, .25)在 Binomial.java 中将使用的递归调用次数。开发一个基于在数组中保存计算值的更好的实现。

网络练习

Sattolo’s algorithm. 编写一个程序 Sattolo.java，使用Sattolo’s algorithm生成一个长度为 N 的均匀分布循环。

Wget. 编写一个程序 Wget.java，从命令行指定的 URL 读取数据并将其保存在同名文件中。

% java Wget http://introcs.cs.princeton.edu/data/codes.csv
% more codes.csv
United States,USA,00
Alabama,AL,01
Alaska,AK,02
...

直角三角形。 编写一个客户端 RightTriangle.java，绘制一个直角三角形和一个外接圆。

% java RightTriangle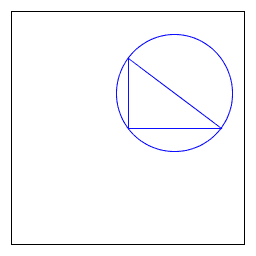
弹跳球。 编写一个程序 BouncingBall.java，演示弹跳球的运动。

<BouncingBall.mov>

您的浏览器不支持视频标记。

1.2 数据抽象

原文：algs4.cs.princeton.edu/12oop

译者：飞龙

协议：CC BY-NC-SA 4.0

面向对象编程。

Java 编程主要基于构建数据类型。这种编程风格被称为面向对象编程，因为它围绕着对象的概念展开，一个持有数据类型值的实体。使用 Java 的原始类型，我们主要限于操作数字的程序，但使用引用类型，我们可以编写操作字符串、图片、声音或 Java 标准库或我们的书站上提供的数百种其他抽象的程序。比预定义数据类型库更重要的是，Java 编程中可用的数据类型范围是开放的，因为您可以定义自己的数据类型。

数据类型。 数据类型 是一组值和对这些值的一组操作。
抽象数据类型。 抽象数据类型 是一个其内部表示对客户端隐藏的数据类型。
对象。 对象是一个可以取一个数据类型值的实体。对象具有三个基本属性：对象的状态是来自其数据类型的值；对象的标识区分一个对象与另一个对象；对象的行为是数据类型操作的效果。在 Java 中，引用是访问对象的机制。
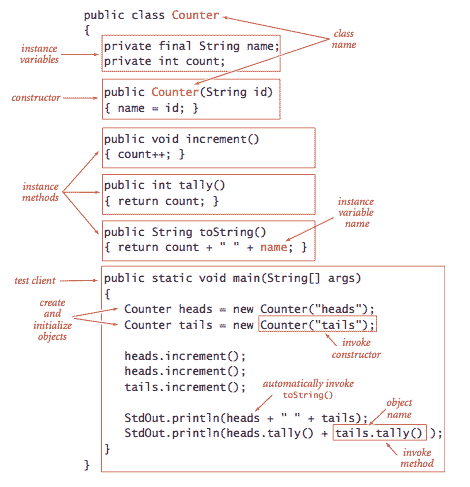
应用程序编程接口（API）。 为了指定抽象数据类型的行为，我们使用一个应用程序编程接口（API），它是一个构造函数和实例方法（操作）的列表，每个操作的效果都有一个非正式描述，就像这个Counter的 API 一样：
客户端。 客户端是使用数据类型的程序。
实现。 实现是实现 API 中指定的数据类型的代码。

使用抽象数据类型。

客户端不需要知道数据类型是如何实现的才能使用它。

创建对象。 每个数据类型值都存储在一个对象中。要创建（或实例化)一个单独的对象，我们通过使用关键字new来调用一个构造函数。每当客户端使用new时，系统会为对象分配内存空间，初始化其值，并返回对对象的引用。
调用实例方法。 实例方法的目的是操作数据类型的值。实例方法具有静态方法的所有属性：参数按值传递，方法名称可以重载，它们可能有返回值，并且可能会引起副作用。它们具有表征它们的附加属性：每次调用都与一个对象关联。
使用对象。 声明为我们提供了在代码中可以使用的对象的变量名。要使用给定的数据类型，我们：
- 声明类型的变量，用于引用对象
- 使用关键字new来调用创建该类型对象的构造函数
- 使用对象名称来调用实例方法，可以作为语句或在表达式中
例如，Flips.java 是一个 Counter.java 客户端，它接受一个命令行参数T并模拟T次硬币翻转。
赋值语句。 具有引用类型的赋值语句会创建引用的副本（而不会创建新对象）��这种情况被称为别名：两个变量都引用同一个对象。别名是 Java 程序中常见的错误来源，如下例所示：
```
Counter c1 = new Counter("ones");
c1.increment();
Counter c2 = c1;
c2.increment(); 
StdOut.println(c1);
```
该代码打印字符串"2 ones"。
对象作为参数。 您可以将对象作为参数传递给方法。Java 将调用程序中的参数值的副本传递给方法。这种安排称为按值传递。如果您将一个指向Counter类型对象的引用传递给方法，Java 将传递该引用的副本。因此，该方法无法更改原始引用（使其指向不同的Counter），但可以更改对象的值，例如通过使用引用调用increment()。
对象作为返回值。 您还可以将对象作为方法的返回值。该方法可能会返回作为参数传递给它的对象，就像 FlipsMax.java 中的情况，或者它可能创建一个对象并返回对其的引用。这种能力很重要，因为 Java 方法只允许一个返回值——使用对象使我们能够编写代码，实际上返回多个值。
数组是对象。 在 Java 中，任何非原始类型的值都是对象。特别是，数组是对象。与字符串一样，对数组有特殊的语言支持：声明、初始化和索引。与任何其他对象一样，当我们将数组传递给方法或在赋值语句的右侧使用数组变量时，我们只是复制数组引用，而不是数组本身的副本。
对象数组。 数组条目可以是任何类型。当我们创建一个对象数组时，需要分两步进行：使用数组构造函数的括号语法创建数组；为数组中的每个对象创建一个标准构造函数。Rolls.java 模拟掷骰子，使用Counter对象数组来跟踪每个可能值出现的次数。

抽象数据类型的示例。

几何对象。 面向对象编程的一个自然示例是为几何对象设计数据类型。
- Point2D.java 是用于平面上的点的数据类型。
- Interval1D.java 是用于一维区间的数据类型。
- Interval2D.java 是用于二维区间的数据类型。
信息处理。 抽象数据类型提供了一个自然的机制来组织和处理信息。信息
- Date.java 是一个表示日期、月份和年份的��据类型。
- Transaction.java 是一个表示客户、日期和金额的数据类型。
累加器。 Accumulator.java 定义了一个 ADT，为客户提供了维护数据值的运行平均值的能力。例如，我们在本书中经常使用这种数据类型来处理实验结果。VisualAccumulator.java 是一个增强版本，还会绘制数据（灰色）和运行平均值（红色）。
字符串。 Java 的String数据类型是一个重要且有用的 ADT。String是char值的索引序列。String有几十种实例方法，包括以下内容：String有特殊的语言支持用于初始化和连接：我们可以使用字符串字面量来创建和初始化字符串，而不是使用构造函数；我们可以使用+运算符来连接字符串，而不是调用concat()方法。
输入和输出再探讨。 第 1.1 节的StdIn、StdOut和StdDraw库的一个缺点是它们限制了我们在任何给定程序中只能使用一个输入文件、一个输出文件和一个绘图。通过面向对象编程，我们可以定义类似的机制，允许我们在一个程序中使用多个输入流、输出流和绘图。具体来说，我们的标准库包括支持多个输入和输出流的数据类型 In.java、Out.java 和 Draw.java。

实现抽象数据类型。

我们使用 Java 类来实现 ADTs，将代码放在与类同名的文件中，后面跟着.java 扩展名。文件中的第一条语句声明实例变量，定义数据类型的值。在实例变量之后是构造函数和实例方法，实现对数据类型值的操作。

实例变量. 为了定义数据类型的值（每个对象的状态），我们声明实例变量的方式与声明局部变量的方式非常相似。每个实例变量对应着许多值（对应数据类型的每个实例对象）。每个声明都由可见性修饰符修饰。在 ADT 实现中，我们使用private，使用 Java 语言机制来强制执行 ADT 的表示应该对客户端隐藏，还可以使用final，如果该值在初始化后不会更改。
构造函数. 构造函数建立对象的标识并初始化实例变量。构造函数总是与类同名。我们可以重载名称并具有具有不同签名的多个构造函数，就像方法一样。如果没有定义其他构造函数，则隐式存在一个默认无参数构造函数，没有参数，并将实例值初始化为默认值。原始数值类型的默认值为 0，boolean为false，null。
实例方法. 实例方法指定数据类型的操作。每个实例方法都有一个返回类型，一个签名（指定其名称和参数变量的类型和名称），以及一个主体（包括一系列语句，包括一个返回语句，将返回类型的值提供给客户端）。当客户端调用方法时，参数值（如果有）将用客户端值初始化，语句将执行直到计算出返回值，并将该值返回给客户端。实例方法可以是public（在 API 中指定）或private（用于组织计算且不可用于客户端）。
作用域. 实例方法使用三种类型的变量：参数变量，局部变量和实例变量。前两者与静态方法相同：参数变量在方法签名中指定，并在调用方法时用客户端值初始化，局部变量在方法主体内声明和初始化。参数变量的作用域是整个方法；局部变量的作用域是定义它们的块中的后续语句。实例变量保存类中对象的数据类型值，其作用域是整个类（在存在歧义时，可以使用this前缀来标识实例变量）。

设计抽象数据类型。

我们将与设计数据类型相关的重要信息放在一个地方供参考，并为本书中的实现奠定基础。

封装. 面向对象编程的一个特点是它使我们能够将数据类型封装在其实现中，以促进客户端和数据类型实现的分开开发。封装实现了模块化编程。
设计 APIs. 在构建现代软件中最重要且最具挑战性的步骤之一是设计 APIs。理想情况下，API 将清晰地阐明所有可能输入的行为，包括副作用，然后我们将有软件来检查实现是否符合规范。不幸的是，理论计算机科学中的一个基本结果，即规范问题，意味着这个目标实际上是不可能实现的。在设计 API 时存在许多潜在的陷阱：
- 过于难以实现，使得开发变得困难或不可能。
- 过于难以使用，导致复杂的客户端代码。
- 过于狭窄，省略了客户端需要的方法。
- 过于广泛，包含许多任何客户端都不需要的方法。
- 过于一般，提供没有用的抽象。
- 过于具体，提供的抽象太过模糊，无用。
- 过于依赖特定表示，因此不能使客户端代码摆脱表示的细节。
总之，为客户端提供他们需要的方法，而不是其他方法。
算法和 ADT. 数据抽象自然适合于算法的研究，因为它帮助我们提供一个框架，可以精确指定算法需要完成的任务以及客户端如何使用算法。例如，我们在本章开头的白名单示例自然地被视为 ADT 客户端，基于以下操作：
- 从给定值数组构造一个 SET。
- 确定给定值是否在集合中。
这些操作封装在 StaticSETofInts.java 和 Allowlist.java 中。
接口继承. Java 提供了语言支持来定义对象之间的关系，称为继承。我们考虑的第一种继承机制称为子类型化，它允许我们通过在接口中指定一组每个实现类必须包含的共同方法来指定否则无关的类之间的关系。我们使用接口继承进行比较和迭代。
实现继承. Java 还支持另一种继承机制，称为子类化，这是一种强大的技术，使程序员能够在不从头开始重写整个类的情况下更改行为和添加功能。这个想法是定义一个��承实例方法和实例变量的新类（子类），从另一个类（超类）继承。我们在本书中避免使用子类化，因为它通常违反封装。这种方法的某些残留物内置在 Java 中，因此不可避免：具体来说，每个类都是Object的子类。
字符串转换. 每种 Java 类型都从Object继承了toString()。这种约定是 Java 自动将连接运算符+的一个操作数转换为String的基础，只要另一个操作数是String。我们通常包含重写默认toString()的实现，如 Date.java 和 Transaction.java。
包装类型. Java 提供了内置的引用类型，称为包装类型，每种原始类型对应一个：

基本类型 包装类型
boolean Boolean
byte Byte
char Character
double Double
float Float
int Integer
long Long
short Short
Java 在必要时会自动将基本类型转换为包装类型（autoboxing）并在需要时转换回来（auto-unboxing）。
相等性. 两个对象相等意味着什么？如果我们用 (a == b) 测试相等性，其中 a 和 b 是相同类型的引用变量，我们正在测试它们是否具有相同的标识：是否引用相等。典型的客户端更希望能够测试数据类型值（对象状态）是否相同。每个 Java 类型都从 Object 继承了 equals() 方法。Java 为标准类型（如 Integer、Double 和 String）以及更复杂类型（如 java.io.File 和 java.net.URL）提供了自然的实现。当我们定义自己的数据类型时，我们需要重写 equals()。Java 的约定是 equals() 必须是一个等价关系：
- 自反性: x.equals(x) 成立。
- 对称性: x.equals(y) 成立当且仅当 y.equals(x) 成立。
- 传递性: 如果 x.equals(y) 和 y.equals(z) 成立，则 x.equals(z) 也成立。
此外，它必须以 Object 作为参数，并满足以下属性。
- 一致性: 多次调用 x.equals(y) 一致地返回相同的值，前提是没有修改任何对象。
- 非空: x.equals(null) 返回 false。
遵循这些 Java 约定可能会有些棘手，就像 Date.java 和 Transaction.java 中所示的那样。
内存管理. Java 最重要的特性之一是其能够自动管理内存。当一个对象不再被引用时，它被称为孤立的。Java 跟踪孤立的对象，并将它们使用的内存返回给一个空闲内存池。以这种方式回收内存被称为垃圾回收。
不可变性. 一个不可变的数据类型具有一个特性，即对象的值在构造后永远不会改变。相比之下，可变的数据类型操作旨在改变的对象值。Java 为帮助强制实现不可变性提供了 final 修饰符。当你声明一个变量为 final 时，你承诺只能在初始化程序或构造函数中为其分配一个值。试图修改 final 变量的值的代码会导致编译时错误。

Vector.java 是一个用于向量的不可变数据类型。为了保证不可变性，它防御性地复制了可变的构造函数参数。
异常和错误是处理我们无法控制的意外错误的破坏性事件。我们已经遇到了以下异常和错误：
- ArithmeticException。当发生异常的算术条件（例如整数除以零）时抛出。
- ArrayIndexOutOfBoundsException。当使用非法索引访问数组时抛出。
- NullPointerException。当需要对象而使用 null 时抛出。
- OutOfMemoryError。当 Java 虚拟机无法分配对象因为内存不足时抛出。
- StackOverflowError。当递归方法递归太深时抛出。
你也可以创建自己的异常。最简单的一种是终止程序执行并打印错误消息的 RuntimeException。
```
throw new RuntimeException("Error message here.");
```
断言是在我们开发的代码中验证我们所做假设的布尔表达式。如果表达式为 false，程序将终止并报告错误消息。例如，假设您有一个计算值，可能用于��引到数组中。如果这个值为负，它将在稍后引起ArrayIndexOutOfBoundsException。但如果您编写代码
```
assert index >= 0; 
```
您可以确定发生错误的地方。默认情况下，断言是禁用的。您可以通过使用-enableassertions标志（简写为-ea）从命令行启用它们。断言用于调试：您的程序不应依赖断言进行正常操作，因为它们可能被禁用。

基本类型	包装类型
`boolean`	Boolean
`byte`	Byte
`char`	Character
`double`	Double
`float`	Float
`int`	Integer
`long`	Long
`short`	Short

Q + A.

Q. Java 中是否有真正的不可变类？

如果使用反射，可以访问任何类的private字段并更改它们。程序 MutableString.java 演示了如何改变一个String。程序 MutableInteger.java 证明了即使实例变量是 final，这也是正确的。

练习

编写一个 Point2D.java 客户端，从命令行获取一个整数值 N，在单位正方形内生成 N 个随机点，并计算最近一对点之间的距离。

以下代码片段打印什么？

String string1 = "hello";
String string2 = string1;
string1 = "world";
StdOut.println(string1);
StdOut.println(string2);

解决方案：

world
hello

如果一个字符串 s 是字符串 t 的circular rotation，那么当字符被任意数量的位置循环移位时，它们匹配；例如，ACTGACG 是 TGACGAC 的循环移位，反之亦然。检测这种条件在基因组序列研究中很重要。编写一个程序，检查两个给定的字符串 s 和 t 是否彼此的循环移位。

解决方案： (s.length() == t.length()) && (s.concat(s).indexOf(t) >= 0)

以下递归函数返回什么？

public static String mystery(String s) {int N = s.length();if (N <= 1) return s;String a = s.substring(0, N/2);String b = s.substring(N/2, N);return mystery(b) + mystery(a);
}

解决方案： 字符串的反转。

使用我们的 Date.java 的实现作为模型，开发一个 Transaction.java 的实现。
使用我们在 Date.java 中的equals()的实现作为模型，为 Transaction.java 开发一个equals()的实现。

创意问题

有理数。 为有理数实现一个不可变的数据类型 Rational.java，支持加法、减法、乘法和除法。您不必担心溢出测试，但使用两个表示分子和分母的long值作为实例变量，以限制溢出的可能性。使用欧几里得算法确保分子和分母永远没有任何公因数。包括一个测试客户端，测试所有方法。
累加器的样本方差。 验证以下代码，为 Accumulator.java 添加var()和stddev()方法，计算作为addDataValue()参数呈现的数字的均值、样本方差和样本标准差。

参考： 这里有一个很好的解释这种一次性方法，最早由 Welford 在 1962 年发现。这种方法可以应用于计算偏度、峰度、回归系数和皮尔逊相关系数。
解析。 为您的 Date.java 和 Transaction.java 实现开发解析构造函数，使用下表中给出的格式的单个String参数指定初始化值。

1.3 袋子、队列和栈

原文：algs4.cs.princeton.edu/13stacks

译者：飞龙

协议：CC BY-NC-SA 4.0

几种基本数据类型涉及对象的集合。具体来说，值的集合是对象的集合，操作围绕向集合中添加、删除或检查对象展开。在本节中，我们考虑了三种这样的数据类型，称为袋子、队列和栈。它们在规定下一个要移除或检查的对象方面有所不同。

API。

我们为袋子、队列和栈定义了 API。除了基础知识外，这些 API 还反映了两个 Java 特性：泛型和可迭代集合。袋子、队列和栈的 API

泛型. 集合 ADT 的一个重要特征是我们应该能够将它们用于任何类型的数据。一种名为泛型的特定 Java 机制实现了这一功能。在我们的每个 API 中类名后面的 <Item> 表示将 Item 命名为 类型参数，一个用于客户端的具体类型的符号占位符。你可以将 Stack<Item> 理解为“项目的堆栈”。例如，你可以编写如下代码
```
Stack<String> stack = new Stack<String>();
stack.push("Test");
...
String next = stack.pop(); 
```
用于 String 对象的堆栈。
自动装箱. 类型参数必须实例化为引用类型，因此 Java 在赋值、方法参数和算术/逻辑表达式中自动在原始类型和其对应的包装类型之间转换。这种转换使我们能够在原始类型中使用泛型，就像以下代码中所示：
```
Stack<Integer> stack = new Stack<Integer>();
stack.push(17);        // autoboxing (int -> Integer)
int i = stack.pop();   // unboxing   (Integer -> int)
```
将基本类型自动转换为包装类型称为 自动装箱，将包装类型自动转换为基本类型称为拆箱。
可迭代集合. 对于许多应用程序，客户端的要求只是以某种方式处理每个项目，或者在集合中迭代。Java 的 foreach 语句支持这种范例。例如，假设 collection 是一个 Queue<Transaction>。那么，如果集合是可迭代的，客户端可以通过一条语句打印交易列表：
```
for (Transaction t : collection)StdOut.println(t);
```
袋子. 一个袋子是一个不支持移除项目的集合——它的目的是为客户提供收集项目并遍历收集项目的能力。Stats.java 是一个袋子客户端，从标准输入读取一系列实数，并打印出它们的平均值和标准差。
FIFO 队列. 一个 FIFO 队列 是基于 先进先出（FIFO）策略的集合。按照任务到达的顺序执行任务的策略在我们日常生活中经常遇到：从在剧院排队等候的人们，到在收费站排队等候的汽车，再到等待计算机应用程序服务的任务。
推入栈. 一个 推入栈 是基于 后进先出（LIFO）策略的集合。当你点击超链接时，浏览器会显示新页面（并将其推入栈）。你可以继续点击超链接访问新页面，但总是可以通过点击返回按钮重新访问上一页（从栈中弹出）。Reverse.java 是一个堆栈客户端，从标准输入读取一系列整数，并以相反顺序打印它们。
算术表达式求值. Evaluate.java 是一个堆栈客户端，用于评估完全括号化的算术表达式。它使用 Dijkstra 的 2 栈算法：
- 将操作数推送到操作数栈上。
- 将运算符推送到运算符栈上。
- 忽略左括号。
- 遇到右括号时，弹出一个运算符，弹出所需数量的操作数，并将将该运算符应用于这些操作数的结果推送到操作数栈上。
这段代码是一个 解释器 的简单示例。

数组和调整大小数组实现集合。

*固定容量的字符串栈。*FixedCapacityStackOfString.java 使用数组实现了一个固定容量的字符串栈。
*固定容量的通用栈。*FixedCapacityStack.java 实现了一个通用的固定容量栈。
数组调整大小栈。ResizingArrayStack.java 使用调整大小数组实现了一个通用栈。使用调整大小数组，我们动态调整数组的大小，使其足够大以容纳所有项目，同时又不会浪费过多空间。如果数组已满，在push()中我们将数组大小加倍；如果数组少于四分之一满，在pop()中我们将数组大小减半。
*数组调整大小队列。*调整大小数组队列.java 使用调整大小数组实现队列 API。

链表。

链表是一种递归数据结构，要么为空（null），要么是指向具有通用项和指向链表的节点的引用。要实现链表，我们从定义节点抽象的嵌套类开始。

private class Node {Item item;Node next;
}

构建链表。 要构建一个包含项目to、be和or的链表，我们为每个项目创建一个Node，将每个节点中的项目字段设置为所需值，并设置next字段以构建链表。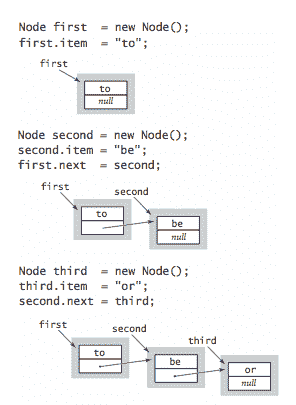
在开头插入。 在链表中插入新节点的最简单位置是在开头。
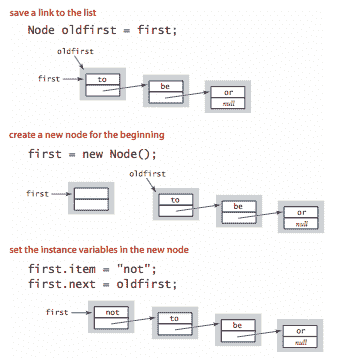
从开头删除。 删除链表中的第一个节点也很容易。
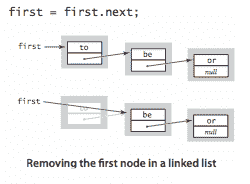
在末尾插入。 要在链表的末尾插入一个节点，我们需要维护一个指向链表中最后一个节点的链接。

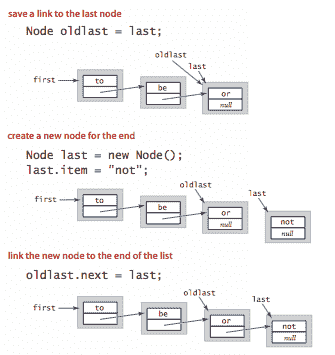
遍历。 以下是遍历链表中节点的习惯用法。

for (Node x = first; x != null; x = x.next) {// process x.item
}

集合的链表实现。

*栈的链表实现。*Stack.java 使用链表实现了一个通用栈。它将栈作为一个链表维护，栈的顶部在开头，由实例变量first引用。要push()一个项目，我们将其添加到列表的开头；要pop()一个项目，我们将其从列表的开头移除。
队列的链表实现。 程序 Queue.java 使用链表实现了一个通用 FIFO 队列。它将队列作为一个链表维护，从最近添加的项目到最近添加的项目的顺序，队列的开始由实例变量first引用，队列的结束由实例变量last引用。要enqueue()一个项目，我们将其添加到列表的末尾；要dequeue()一个项目，我们将其从列表的开头移除。
背包的链表实现。 程序 Bag.java 使用链表实现了一个通用背包。该实现与 Stack.java 相同，只是将push()的名称更改为add()并删除pop()。

迭代。

要考虑实现迭代的任务，我们从一个客户端代码片段开始，该代码打印字符串集合中的所有项目，每行一个：

Stack<String> collection = new Stack<String>();
...
for (String s : collection)StdOut.println(s);
...

这个foreach语句是以下while语句的简写：

Iterator<String> i = collection.iterator();
while (i.hasNext()) { String s = i.next();StdOut.println(s);
}

要在集合中实现迭代：

包含以下import语句，以便我们的代码可以引用 Java 的java.util.Iterator接口：
```
import java.util.Iterator;
```
将以下内容添加到类声明中，承诺提供一个iterator()方法，如Java.lang.Iterable接口中指定的：
```
implements Iterable<Item>
```
实现一个返回实现Iterator接口的类的对象的方法iterator()：
```
public Iterator<Item> iterator() {return new LinkedIterator();
}
```
实现一个嵌套类，通过包含hasNext()、next()和remove()方法来实现Iterator接口。我们总是对可选的remove()方法使用空方法，因为最好避免在迭代中插入修改数据结构的操作。
- 当底层数据结构是链表时，Bag.java 中的嵌套类LinkedIterator说明了如何实现一个实现Iterator接口的类。
- 当底层数据结构是数组时，ResizingArrayBag.java 中的嵌套类ArrayIterator也是如此。

自动装箱问题 + 回答

Q. 自动装箱如何处理以下代码片段？

Integer a = null;
int b = a;

A. 这导致运行时错误。原始类型可以存储其对应包装类型的每个值，除了null。

Q. 为什么第一组语句打印true，但第二组打印false？

Integer a1 = 100;
Integer a2 = 100;
System.out.println(a1 == a2);   // trueInteger b1 = new Integer(100);
Integer b2 = new Integer(100);
System.out.println(b1 == b2);   // falseInteger c1 = 150;
Integer c2 = 150;
System.out.println(c1 == c2);   // false

A. 第二个打印false，因为b1和b2是指向不同 Integer 对象的引用。第一个和第三个代码片段依赖于自动装箱。令人惊讶的是，第一个打印 true，因为在-128 和 127 之间的值似乎指向相同的不可变 Integer 对象（Java 的valueOf()实现在整数在此范围内时检索缓存值），而 Java 为此范围外的每个整数构造��对象。

这里是另一个 Autoboxing.java 的异常。

泛型问题 + 回答

Q. 泛型仅用于自动转换吗？

A. 不是，但我们只会用于“具体参数化类型”，其中每种数据类型都由单个类型参数化。主要好处是在编译时而不是运行时发现类型不匹配错误。泛型还有其他更一般（更复杂）的用途，包括通配符。这种一般性对于处理子类型和继承很有用。有关更多信息，请参阅这个泛型常见问题解答和这个Java 泛型教程。

Q. 具体参数化类型可以像普通类型一样使用吗？

A. 是的，有几个例外情况（数组创建、异常处理、使用instanceof和在类文字中）。

Q. 我可以将 Node 类设为静态吗？

A. 对于 LinkedStackOfString.java，你可以这样做而不需要其他更改，并节省每个节点的 8 字节（内部类开销）。然而，在 LinkedStack.java 中的嵌套类Node使用外部类的Item类型信息，因此你需要做一些额外的工作使其静态化。Stack.java 通过使嵌套类（和嵌套迭代器）泛型化来实现这一点：有三个单独的泛型类型参数，每个都命名为Item。

Q. 当我尝试创建泛型数组时为什么会出现“无法创建泛型数组”的错误？

public class ResizingArrayStack<Item> {Item[] a = new Item[1];

A. 不幸的是，在 Java 1.5 中无法创建泛型数组。根本原因是 Java 中的数组是协变的，但泛型不是。换句话说，String[]是Object[]的子类型，但Stack<String>不是Stack<Object>的子类型。为了解决这个缺陷，你需要执行一个未经检查的转换，就像在 ResizingArrayStack.java 中一样。ResizingArrayStackWithReflection.java 是一个（笨拙的）替代方案，通过使用反射来避免未经检查的转换。

Q. 那么，为什么数组是协变的？

A. 许多程序员（和编程语言理论家）认为 Java 类型系统中的协变数组是一个严重的缺陷：它们会产生不必要的运行时性能开销（例如，参见ArrayStoreException），并且可能导致微妙的错误。Java 引入协变数组是为了解决 Java 最初设计中不包含泛型的问题，例如，实现Arrays.sort(Comparable[])并使其能够接受String[]类型的输入数组。

Q. 我可以创建并返回一个参数化类型的新数组吗，例如为泛型队列实现一个toArray()方法？

A. 不容易。你可以使用反射来实现，前提是客户端向toArray()传递所需具体类型的对象。这是 Java 集合框架采取的（笨拙的）方法。GenericArrayFactory.java 提供了一个客户端传递Class类型变量的替代解决方案。另请参阅 Neal Gafter 的博客，了解使用type tokens的解决方案。

迭代器问答

Q. 为什么这个结构被称为foreach，而它使用关键字for？

A. 其他语言使用关键字foreach，但 Java 开发人员不想引入新关键字并破坏向后兼容性。

Q. String可迭代吗？

A. 不。

Q. 数组是Iterable吗？

A. 不。你可以使用它们的 foreach 语法。但是，你不能将数组传递给期望Iterable的方法，也不能从返回Iterable的方法返回数组。这样会很方便，但实际上不起作用。

Q. 以下代码片段有什么问题？

String s;
for (s : listOfStrings)System.out.println(s);

A. 增强的 for 循环要求在循环内部声明迭代变量。

练习

在 FixedCapacityStackOfStrings.java 中添加一个isFull()方法。
给出java Stack对输入打印的输出
```
it was - the best - of times - - - it	was - the - -
```
解决方案。was best times of the was the it (1 left on stack)

假设执行了一系列交错的（栈）push和pop操作。push 操作按顺序将整数 0 到 9 推入栈；pop 操作打印返回值。以下哪种序列不可能发生？

(a)  4 3 2 1 0 9 8 7 6 5(b)  4 6 8 7 5 3 2 9 0 1(c)  2 5 6 7 4 8 9 3 1 0(d)  4 3 2 1 0 5 6 7 8 9(e)  1 2 3 4 5 6 9 8 7 0(f)  0 4 6 5 3 8 1 7 2 9(g)  1 4 7 9 8 6 5 3 0 2(h)  2 1 4 3 6 5 8 7 9 0

答案：(b)、(f)和(g)。

编写一个栈客户端 Parentheses.java，从标准输入中读取一系列左右括号、大括号和方括号，并使用栈来确定序列是否平衡。例如，你的程序应该对[()]{}{[()()]()}打印true，对[(])打印false。

当n为 50 时，以下代码片段打印什么？给出当给定正整数n时它的高级描述。

Stack<Integer> s = new Stack<Integer>();
while (n > 0) {s.push(n % 2);n = n / 2;
}
while (!s.isEmpty())System.out.print(s.pop());
System.out.println();

答案：打印N的二进制表示（当n为50时为110010）。

以下代码片段对队列q做了什么？

Stack<String> s = new Stack<String>();
while(!q.isEmpty())s.push(q.dequeue());
while(!s.isEmpty())q.enqueue(s.pop());

答案：颠倒队列中的项目。

在 Stack.java 中添加一个peek方法，返回栈中最近插入的项（不弹出）。
编写一个过滤器程序 InfixToPostfix.java，将中缀算术表达式转换为后缀表达式。
编写一个程序 EvaluatePostfix.java，从标准输入中获取后缀表达式，对其进行评估，并打印值。（将上一个练习的程序输出通过管道传递给这个程序，可以实现与 Evaluate.java 相同的行为。）
假设客户端执行了一系列交错的（队列）enqueue和dequeue操作。enqueue 操作按顺序将整数 0 到 9 放入队列；dequeue 操作打印返回值。以下哪种序列不可能发生？
```
(a)  0 1 2 3 4 5 6 7 8 9(b)  4 6 8 7 5 3 2 9 0 1 (c)  2 5 6 7 4 8 9 3 1 0(d)  4 3 2 1 0 5 6 7 8 9
```
答案：(b)、©和(d)。
开发一��类 ResizingArrayQueueOfStrings，使用固定大小数组实现队列抽象，然后扩展您的实现以使用数组调整大小以消除大小限制。

解决方案: ResizingArrayQueue.java

链表练习

创意问题

约瑟夫问题。 在古代的约瑟夫问题中，N 个人陷入困境，并同意采取以下策略来减少人口。他们围成一个圆圈（位置从 0 到 N-1 编号），沿着圆圈进行，每隔 M 个人就淘汰一个，直到只剩下一个人。传说中约瑟夫找到了一个位置可以避免被淘汰。编写一个 Queue 客户端 Josephus.java，从命令行获取 M 和 N，并打印出人们被淘汰的顺序（从而向约瑟夫展示在圆圈中应该坐在哪里）。
```
 % java Josephus 2 7
1 3 5 0 4 2 6
```

复制一个栈。 为链表实现的 Stack.java 创建一个新的构造函数，使得 Stack t = new Stack(s) 使 t 引用栈 s 的一个新且独立的副本。

递归解决方案: 为从给定 Node 开始的链表创建一个复制构造函数，并使用它来创建新的栈。

Node(Node x) {item = x.item;if (x.next != null) next = new Node(x.next);
}public Stack(Stack<Item> s) { first = new Node(s.first); }

非递归解决方案: 为单个 Node 对象创建一个复制构造函数。

Node(Node x) { this.item = x.item; this.next = x.next; }public Stack(Stack<Item> s) {if (s.first != null) {first = new Node(s.first);for (Node x = first; x.next != null; x = x.next)x.next = new Node(x.next);}
}

栈的可生成性。 假设我们有一个混合 push 和 pop 操作的序列，就像我们的测试栈客户端一样，其中按顺序 0、1、…、N-1（push 指令）与 N 个减号（pop 指令）交错。设计一个算法，确定混合序列是否会导致栈下溢。（您只能使用与 N 无关的空间量 - 不能将整数存储在数据结构中。）设计一个线性时间算法，确定给定排列是否可以由我们的测试客户端生成输出（取决于 pop 操作发生的位置）。

解决方案。 只有存在整数 k，使得前 k 个 pop 操作发生在前 k 个 push 操作之前，栈才会下溢。

如果可以生成给定的排列，那么它将唯一生成如下：如果排列中的下一个整数在栈的顶部，则弹出它；否则，将输入序列中的下一个整数推送到栈上（或者如果已经推送了 N-1，则停止）。只有在终止时栈为空，排列才能生成。
栈可生成的禁止三元组。 (R. Tarjan) 证明排列可以由栈生成（如前一个问题中所述），当且仅当它没有 禁止的三元组 (a, b, c)，其中 a < b < c，c 第一，a 第二，b 第三（可能在 c 和 a 之间以及 a 和 b 之间有其他插入的整数）。

部分解决方案。 假设存在一个禁止的三元组（a，b，c）。在 a 和 b 之前弹出项 c，但在 c 之前推入 a 和 b。因此，当推入 c 时，a 和 b 都在栈上。因此，在弹出 b 之前，a 不能被弹出。
可连接的队列、栈或 steque。 添加一个额外的连接操作，（破坏性地）连接两个队列、栈或 steques。提示: 使用循环链表，保持指向最后一项的指针。
快速失败的迭代器。 修改 Stack.java 中的迭代器代码，如果客户端在迭代期间修改集合（通过 push() 或 pop()）则立即抛出 java.util.ConcurrentModificationException。

解决方案: 维护一个计数器，计算 push() 和 pop() 操作的次数。创建一个迭代器时，将此值存储为迭代器实例变量。在每次调用 hasNext() 和 next() 之前，检查该值是否自构造迭代器以来已更改；如果已更改，则抛出异常。
带优先级的表达式求值。 编写一个程序 EvaluateDeluxe.java，扩展 Evaluate.java 以处理未完全括号化的表达式，使用标准的运算符 +、-、* 和 / 的优先级顺序。

网络练习

尾部。 编写一个程序 Tail，使得 Tail k < file.txt 打印文件 file.txt 的最后 k 行。使用 StdIn.readLine()。应该使用哪种数据结构？
有界栈。 一个有界栈是一个最多容纳 N 个元素的栈。（应用：带有有限缓冲区的撤销或历史记录。）
删除第 i 个元素。 创建一个支持以下操作的数据类型：isEmpty、insert 和 remove(int i)，其中删除操作删除并返回队列中最近添加的第 i 个对象。首先使用数组实现，然后使用链表实现。每个操作的运行时间是多少？
动态缩小。 使用栈和队列的数组实现时，当数组不足以存储下一个元素时，我们会将数组大小加倍。如果我们执行了多次加倍操作，然后删除了很多元素，可能会得到一个比必要的大得多的数组。实现以下策略：每当数组的填充率低于 1/4 时，将其缩小到一半大小。解释为什么当填充率低于 1/2 时我们不将其缩小到一半大小。
栈 + 最大值。 创建一个数据结构，有效支持栈操作（弹出和推入），并返回最大元素。假设元素是整数或实数，以便可以比较它们。

提示：使用两个堆栈，一个用于存储所有元素，另一个用于存储最大值。
PostScript。 PostScript 是大多数打印机使用的基于堆栈的语言。使用一个堆栈实现 PostScript 的一个小子集。
面试问题。 给定一个未知数量的字符串的堆栈，打印出倒数第 5 个字符串。在此过程中破坏堆栈是可以的。提示：使用一个包含 5 个元素的队列。
标签系统。 编写一个程序，从命令行读取一个二进制字符串，并应用以下（00, 1101��标签系统：如果第一个位是 0，则删除前三位并追加 00；如果第一个位是 1，则删除前三位并追加 1101。只要字符串至少有 3 位，就重复此过程。尝试确定以下输入是否会停止或进入无限循环：10010, 100100100100100100。使用一个队列。
图灵带。 实现一个一维图灵带。带由一系列单元格组成，每个单元格存储一个整数（初始化为 0）。在任何时刻，都有一个带头指向其中一个单元格。支持以下接口方法：moveLeft 将带头向左移动一个单元格，moveRight 将带头向右移动一个单元格，look 返回活动单元格的内容，write(int a) 将活动单元格的内容更改为 a。提示：使用一个 int 表示活动单元格，使用两个堆栈表示带的左侧和右侧部分。类似于文本编辑器缓冲区。
回文检查器。 编写一个程序，读取一系列字符串并检查它们是否构成回文。忽略标点、空格和大小写。（A MAN, A PLAN, A CANAL - PANAMA）。使用一个栈和一个队列。
流算法。 给定一长序列的项目，设计一个数据结构来存储最近看到的 k 个项目。
2 M/M/1 队列。 下一个顾客被分配到两个队列中较小的一个。使用 2 个先进先出队列。当接近收费站时，总是选择较长的队列（或错误的车道）的感觉。假设两辆车同时进入收费站并选择相同长度的不同队列。计算一辆车领先另一辆车的平均时间长度。
M/M/k 队列。 比较 k 个独立的 M/M/1 队列和 M/M/k 队列。
M/G/1 队列。 分析具有不同服务分布（G = 一般）的排队模型。
中缀表达式转后缀表达式并考虑优先级顺序。 编写一个程序将中缀表达式转换为后缀表达式。从左到右扫描中缀表达式。
- 操作数：输出它。
- 左括号：推入栈中。
- 右括号：重复弹出栈中的元素并输出，直到遇到左括号。丢弃两个括号。
- 优先级高于栈顶的运算符：推入栈中。
- 优先级低于或等于栈顶的运算符：重复弹出栈中的元素并输出，直到栈顶的运算符具有更高的优先级。将扫描到的运算符推入栈中。之后，弹出栈中的剩余元素并输出。
检查重复。 编写一个代码片段，确定一个袋子是否包含任何重复项目。使用两个嵌套迭代器。
检查三重复。 编写一个代码片段，确定一个袋子是否包含至少三次重复的项目。使用三重嵌套迭代器。
相等。 如果两个队列按相同顺序包含相同项目，则它们相等。如果两个袋子包含相同项目但顺序不同，则它们相等。
整数集合。 创建一个表示 0 到 N-1 之间（无重复）整数集合的数据类型。支持add(i)，exists(i)，remove(i)，size()，intersect，difference，symmetricDifference，union，isSubset，isSuperSet和isDisjointFrom。包括一个迭代器。
冒号。 有经验的程序员知道，像下面这样写一个循环通常是一个坏主意
```
for (double x = 0.0; x <= N; x += 0.1) {..
}
```
由于浮点精度的结果，如果 N = xxx，则循环将执行 10N 次，如果 N = yyy，则执行 10N + 1 次。创建一个数据类型Mesh，使得x从left到right以delta的大小增量。假设right >= left，则循环应该恰好执行1 + floor((right - left) / delta)次。
```
for (double x : new Mesh(left, right, delta)) {..
}
```
这是 MATLAB 中冒号运算符的工作原理。您还应该对程序进行调试，以确保即使left > right且delta为负数也能正常工作。
列表迭代器。 我们可能还想包括用于在列表中向后移动的方法hasPrevious()和previous()。要实现previous()，我们可以使用双向链表。程序 DoublyLinkedList.java 实现了这种策略。它使用 Java 的java.util.ListIterator接口支持向前和向后移动。我们实现了所有可选方法，包括remove()，set()和add()。remove()方法删除next()或previous()返回的最后一个元素。set()方法覆盖next()或previous()返回的最后一个元素的值。add()方法在next()将返回的下一个元素之前插入一个元素。只有在调用next()或previous()之后，且没有调用remove()或add()之后，才能调用set()和remove()是合法的。

我们使用一个虚拟的头节点和尾节点来避免额外的情况。我们还存储一个额外的变量lastAccessed，它存储在最近一次调用next()或previous()时访问的节点。删除元素后，我们将lastAccessed重置为null；这表示调用remove()是非法的（直到随后调用next()或previous()为止）。
双向迭代器。 定义一个支持四种方法的接口TwoWayIterator：hasNext()，hasPrevious()，next()和previous()。实现一个支持TwoWayIterator的列表。提示：使用数组或双向链表实现列表。
将一个袋子添加到另一个末尾。 编写一个方法，将一个袋子 b 的项目添加到调用方的末尾。假设两个袋子存储相同类型的项目。

提示：使用迭代器遍历 b 的项目，并将每个项目添加到调用方的末尾。
替换所有。 编写一个方法，在队列或栈中用项目from替换所有出现的项目to。
将列表添加到自身。 以下代码片段的结果是什么？
```
List list1 = new ArrayList();
List list2 = new ArrayList();
list1.add(list2);
list2.add(list1);
System.out.println(list1.equals(list2));List list = new ArrayList();
list.add(list);
System.out.println(list.hashCode());
```
答案： 栈溢出。Java 文档中说：“虽然列表可以包含自身作为元素，但极度谨慎是明智的：在这样的列表上，equals 和 hashCode 方法不再被很好地定义。”
歌曲播放列表。 创建一个支持以下操作的数据类型：enqueue（将新歌曲添加到列表末尾）、play（打印下一首歌曲的名称）、skip（跳过列表中的下一首歌曲，不打印其名称）和back（返回上一首歌曲）。使用支持前向和后向迭代器的列表。
Josephus。 程序 Josephus.java 计算 Josephus 数。
以下代码会按升序打印出整数 0 到 9 吗？
```
int[] vals = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
for (int val : vals) {System.out.print(val + " ");StdRandom.shuffle(vals);     // mutate the array while iterating
}
System.out.println();
```
不会。它会打印出 10 个值，但会有一些重复项，并且不会按升序排列。迭代器不会保存原始数组的副本 - 相反，它使用已变异的副本。
使用一个访问指针实现队列。 重新实现一个队列，所有操作都需要恒定时间，但只有一个实例变量（而不是两个）。提示： 使用循环链表，保持指向最后一个项目的指针。
Steque。 栈结束队列或steque是一种支持 push、pop 和 enqueue 的数据类型。Knuth 将其称为输出受限双端队列。使用单链表实现它。
使用两个栈实现队列。 实现一个使用两个栈的队列，使得每个队列操作都需要恒定的摊销栈操作次数。提示： 如果你将元素推入栈然后全部弹出，它们会以相反顺序出现。如果你重复这个过程，它们现在又会按顺序排列。

*解决方案：*QueueWithTwoStacks.java。
使用恒定数量的栈实现队列。 实现一个使用恒定数量的栈的队列，使得每个队列操作都需要恒定（最坏情况）的栈操作次数。警告： 难度非常高。
使用队列实现栈。 实现一个使用单个队列的栈，使得每个栈操作都需要线性数量的队列操作。提示： 要删除一个项目，逐个获取队列中的所有元素，并将它们放在末尾，除了最后一个应该删除并返回。（诚然非常低效。）
使用 Deque 实现两个栈。 使用单个 Deque 实现两个栈，使得每个操作都需要恒定数量的 Deque 操作。
使用两个栈实现 Steque。（R. Tarjan） 实现一个使用两个栈的 Steque，使得每个 Steque 操作都需要恒定的摊销栈操作次数。
使用栈和 Steque 实现 Deque。（R. Tarjan） 实现一个使用栈和 Steque 的 Deque，使得每个 Deque 操作都需要恒定的摊销栈和 Steque 操作次数。
使用三个栈实现 Deque。（R. Tarjan） 实现一个使用三个栈的 Deque，使得每个 Deque 操作都需要恒定的摊销栈操作次数。
多词搜索。 程序 MultiwordSearch.java 从命令行读取查询词 q[1]，…，q[k]的序列，从标准输入读取文档单词 d[1]，…，d[N]的序列，并找到这些 k 个单词按相同顺序出现的最短间隔。（这里最短意味着间隔中的单词数。）即找到索引 i 和 j，使得 d[i1] = q[1]，d[i2] = q[2]，…，d[ik] = q[k]，且 i1 < i2 < … < ik。

答案：对于每个查询词，创建一个在文档中出现的索引的排序列表。按照 2 到 k 的顺序扫描列表，删除每个列表前面的索引，直到生成的 k 个列表的第一个元素按升序排列。
```
q[1]: 50 123 555 1002 1066
q[2]: 33 44 93 333 606 613
q[3]: 60 200
q[4]: 12 18 44 55 203 495q[1]: 50 123 555 1002 1066
q[2]: 93 333 606 613
q[3]: 200
q[4]: 203 495
```
列表 1 上的第一个元素序列形成包含列表 1 上第一个元素的最短间隔。

现在删除列表 1 上的第一个元素。重复删除列表 2 中的元素，直到它与列表 1 一致。对列表 3 重复此操作，直到整个数组按升序排列。检查这个序列的第一个元素等等。
M/M/1 队列. 马尔可夫/马尔可夫/单服务器模型是运筹学和概率论中的基本排队模型。任务以特定速率 λ 按泊松过程到达。这意味着每小时到达 λ 个顾客。��具体地说，到达遵循均值为 1 / λ 的指数分布：在时间 0 和 t 之间到达 k 个的概率是 (λ t)^k e^(-λ t) / k!。任务按照率为 μ 的泊松过程按 FIFO 顺序服务。两个 M 代表马尔可夫：这意味着系统是无记忆的：到达之间的时间是独立的，离开之间的时间也是独立的。

M/M/1 模型分析。我们感兴趣的是理解排队系统。如果 λ > μ，则队列大小会无限增加。对于像 M/M/1 这样的简单模型，我们可以使用概率论来分析这些数量。假设 μ > λ，系统中恰好有 n 个顾客的概率是 (λ / μ)^n (1 - λ / μ)。
- L = 系统中平均顾客数量 = λ / (μ - λ).
- L[Q] = 队列中平均顾客数量 = λ² / (μ (μ - λ)).
- W = 顾客在系统中的平均时间 = 1 / (μ - λ).
- W[Q] = 顾客在队列中的平均时间 = W - 1 / μ.
程序 MM1Queue.java 对于更复杂的模型，我们需要使用这样的模拟。变体：多个队列，多个服务器，顺序多级服务器，使用有限队列并测量被拒绝的顾客数量。应用：麦当劳的顾客，互联网路由器中的数据包，
列出文件. Unix 目录是文件和目录的列表。程序 Directory.java 接受目录名称作为命令行参数，并按级别顺序打印出该目录中包含的所有文件（以及任何子目录）。它使用一个队列。
中断处理. 当编写可以被中断的实时系统（例如，通过鼠标点击或无线连接）时，有必要立即处理中断，然后再继续当前活动。如果中断应按照到达顺序处理，则 FIFO 队列是适当的数据结构。
库实现. Java 有一个名为 Stack 的内置库，但您应该避免使用它。它具有不通常与堆栈相关联的附加操作，例如获取第 i 个元素和将元素添加到堆栈底部（而不是顶部）。尽管具有这些额外操作可能看起来是一个奖励，但实际上是一个诅咒。我们使用 ADT 不是因为它们提供了每个可用的操作，而是因为它们限制了我们可以执行的操作类型！这可以防止我们执行我们实际上不想要的操作。如果我们需要的不仅仅是 LIFO 访问，我们应该使用不同的数据类型。我们仍然可以从 Java 库构建一个堆栈数据类型，但我们要小心限制操作类型。没有 Java 队列实现。
负载平衡. N 个用户必须在网络中的 N 个相同服务器中进行选择。目标：平衡用户在资源之间的分布。检查每个资源以找到一个空闲的（或最不忙的）资源太昂贵了。相反，选择一个随机服务器。在任何步骤中，您应该能够看到每台机器上的作业。程序 Server.java 绘制负载分布。理论：平均负载 = 1，最大负载 = log N / log log N。
负载平衡再加载. (Azar, Broder, Karlin, and Upfal) 选择两个随机资源。插入到两者中最不忙的资源上。理论：平均负载 = 1，最大负载 = log log N。
*网格化。*给定单位盒中的 N 个欧几里得点和参数 d，找到所有距离 d 以内的点对。将盒子分成一个 G×G 的网格，其中 G = ceil(1/d)。将所有点放入给定网格单元格中的列表。任何距离 d 以内的邻居必须在该单元格或其 8 个邻居之一中。程序 Grid.java 使用辅助数据类型 Point2D.java 实现了这种策略。
*Java 库。*Java 包含库类LinkedList和ArrayList，实现了一个列表。比我们的Sequence数据类型具有更广泛的接口：通过索引访问元素，删除元素，搜索元素。没有 urns。
为Stack添加一个名为dup()的方法，用于创建顶部元素的副本并将其推入栈中。
为Stack添加一个名为exch()的方法，用于交换栈顶部的两个元素。
为Stack添加一个名为size()的方法，返回栈中的元素数量。
为Stack添加一个名为Item[] multiPop(int k)的方法，从栈中弹出 k 个元素并将它们作为对象数组返回。
为Queue添加一个名为Item[] toArray()的方法，将队列中的所有 N 个元素作为长度为 N 的数组返回。
编写一个递归函数，该函数以队列作为输入，并重新排列队列，使其顺序相反。提示：出队第一个元素，递归反转队列，然后入队第一个元素。
给定一个队列，创建两个新队列 q1 和 q2，使得 q1 包含 q 的偶数元素，q2 包含奇数元素，例如，就像处理一副牌一样。

以下代码片段做什么？

Queue<Integer> q = new Queue<Integer>();
q.enqueue(0);
q.enqueue(1);
for (int i = 0; i < 10; i++) {int a = q.dequeue();int b = q.dequeue();q.enqueue(b);q.enqueue(a + b);System.out.println(a);
}

在文字处理器中实现“撤销”功能，您会选择哪种数据类型来实现？
假设您有一个大小为 N 的单个数组，并且希望实现两个栈，以便在两个栈上的元素总数为 N+1 之前不会溢出。您将如何实现这一点？
假设您在 Stack.java 的链表实现中使用以下代码实现push。错误在哪里？
```
public void push(Item item) {Node second = first;Node first = new Node();first.item = item;first.next = second;
}
```
答案：通过重新声明first，您创建了一个名为first的新局部变量，它与名为first的实例变量不同。
**最小栈。**设计一个数据类型，实现以下操作，所有操作都在常数时间内完成：推送，弹出，最小值。假设项目是Comparable的。

解决方案：维护两个栈，一个包含所有项目，另一个包含最小值。要推送项目，请将其推送到第一个栈；如果它小于第二个栈的顶部项目，请将其也推送到第二个栈。要弹出项目，请从第一个栈弹出；如果它是第二个栈的顶部项目，请也从第二个栈弹出。要找到最小值，请返回第二个栈的顶部项目。
**翻倍和减半。**将 ResizingArrayStack.java 中的减半测试从if (N > 0 && N == a.length/4) resize(a.length/2);替换为if (N == a.length/4) resize(2*N);的效果是什么？
**Shunting-yard 算法。**实现 Dijkstra 的shunting-yard 算法将中缀表达式转换为后缀表达式。支持运算符优先级，包括左结合和右结合运算符。
**FIFO 队列与随机删除。**实现一个数据类型，支持插入一个项目，删除最近添加的项目和删除一个随机项目。每个操作应该在每次操作中花费常数期望摊销时间，并且应该使用空间（最多）与数据结构中的项目数量成比例。
**股票价格。**给定每日股票价格数组prices[]，创建一个数组days[]，使得days[i]告诉您从第i天开始，直到股票价格超过prices[i]需要等待多少天。

提示：你的算法应该以线性时间运行，并使用一个数组索引的栈。

1.4 算法分析

原文：algs4.cs.princeton.edu/14analysis

译者：飞龙

协议：CC BY-NC-SA 4.0

随着人们在使用计算机方面的经验增加，他们用计算机来解决困难问题或处理大量数据，不可避免地会引发这样的问题：

我的程序需要多长时间？
为什么我的程序会耗尽内存？

科学方法。

科学家用来理解自然界的方法同样适用于研究程序的运行时间：

观察自然界的某些特征，通常是通过精确的测量。
假设一个与观察一致的模型。
使用假设预测事件。
通过进一步观察验证预测。
通过重复直到假设和观察一致来验证。

我们设计的实验必须是可重复的，我们制定的假设必须是可证伪的。

观察。

我们的第一个挑战是确定如何对程序的运行时间进行定量测量。Stopwatch.java 是一种测量程序运行时间的数据类型。秒表 API ThreeSum.java 计算一个包含 N 个整数的文件中总和为 0 的三元组的数量（忽略整数溢出）。DoublingTest.java 生成一系列随机输入数组，每一步将数组大小加倍，并打印 ThreeSum.count() 的运行时间。DoublingRatio.java 类似，但还输出从一个大小到下一个大小的运行时间比率。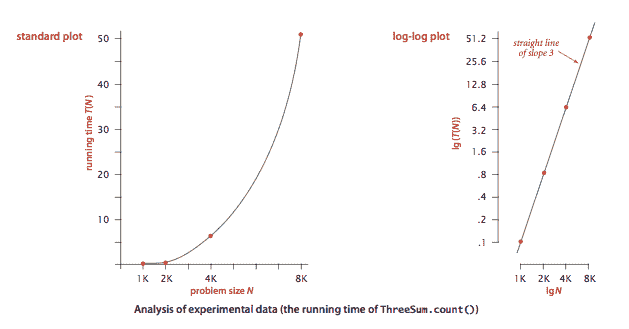运行时间的对数图

数学模型。

一个程序的总运行时间由两个主要因素决定：执��每个语句的成本和每个语句的执行频率。

波浪线近似。 我们使用波浪线近似，其中我们丢弃复杂化公式的低阶项。我们写 ~ f(N) 来表示任何函数，当除以 f(N) 时，随着 N 的增长趋近于 1。我们写 g(N) ~ f(N) 来表示当 N 增长时，g(N) / f(N) 趋近于 1。
增长顺序分类。 我们通常使用形式为 g(N) ~ a f(N) 的波浪线近似，其中 f(N) = N^b log^c N，并将 f(N) 称为 g(N) 的增长顺序。我们只使用几个结构原语（语句、条件、循环、嵌套和方法调用）来实现算法，因此成本的增长顺序往往是问题大小 N 的几个函数之一。
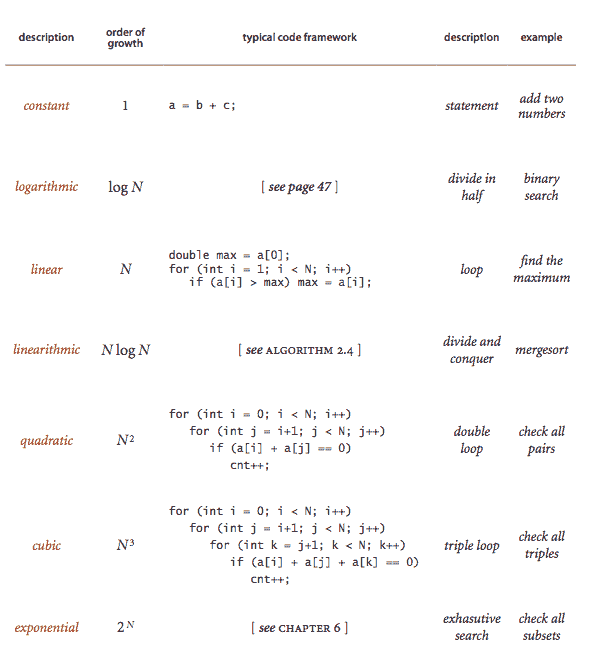
成本模型。 我们通过阐明定义基本操作的成本模型来关注算法的属性。例如，对于 3-sum 问题，一个适当的成本模型是我们访问数组条目的次数，无论是读取还是写入。

性质。 ThreeSum.java 的运行时间增长顺序为 N³。

命题。 暴力 3-sum 算法使用*~ N³ / 2* 数组访问来计算在 N 个数字中总和为 0 的三元组的数量。

设计更快的算法。

研究程序增长顺序的一个主要原因是帮助设计更快的算法来解决相同的问题。使用归并排序和二分查找，我们为 2-sum 和 3-sum 问题开发了更快的算法。

2-sum. 暴力解决方案 TwoSum.java 需要的时间与 N² 成正比。TwoSumFast.java 在时间上与 N log N 成正比地解决了 2-sum 问题。
3-sum. ThreeSumFast.java 在时间上与 N² log N 成正比地解决了 3-sum 问题。

处理对输入的依赖。

对于许多问题，运行时间可能会根据输入而有很大的变化。

输入模型. 我们可以仔细地对要处理的输入类型进行建模。这种方法具有挑战性，因为模型可能是不现实的。
最坏情况性能保证. 程序的运行时间小于某个界限（作为输入大小的函数），无论输入是什么。这种保守的方法可能适用于运行核反应堆、心脏起搏器或汽车刹车的软件。
随机算法. 提供性能保证的一种方法是引入随机性，例如快速排序和哈希。每次运行算法时，它都会花费不同的时间。这些保证并不是绝对的，但它们无效的几率小于你的计算机被闪电击中的几率。因此，这些保证在实践中与最坏情况的保证一样有用。
摊销分析. 对于许多应用程序，算法的输入可能不仅仅是数据，还包括客户端执行的操作序列。摊销分析提供了对操作序列的最坏情况性能保证。

命题. 在Bag、Stack和Queue的链表实现中，所有操作在最坏情况下都需要常数时间。

命题. 在Bag、Stack和Queue的调整大小数组实现中，从空数据结构开始，任何长度为N的操作序列在最坏情况下需要与N成比例的时间（摊销每个操作的常数时间）。

内存使用。

要估算我们的程序使用了多少内存，我们可以计算变量的数量，并根据它们的类型按字节加权。对于典型的 64 位机器，

原始类型. 下表给出了原始类型的内存需求。
对象. 要确定对象的内存使用量，我们将每个实例变量使用的内存量加到与每个对象相关联的开销上，通常为 16 字节。此外，内存使用量通常会填充为 8 字节的倍数（在 64 位机器上）。
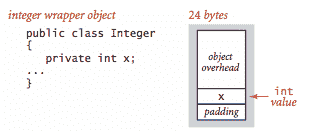
参考文献. 对象的引用通常是一个内存地址，因此在 64 位机器上使用 8 字节的内存。
链表. 嵌套的非静态（内部）类，比如我们的Node类，需要额外的 8 字节开销（用于引用封闭实例）。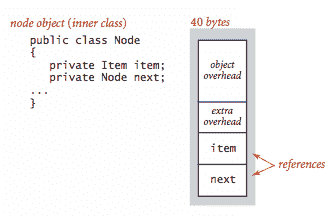
数组. Java 中的数组被实现为对象，通常需要额外的开销来存储长度。原始类型值的数组通常需要 24 字节的头信息（16 字节的对象开销，4 字节的长度，和 4 字节的填充），再加上存储值所需的内存。
字符串. Java 7 中长度为N的字符串通常使用 32 字节（用于String对象），再加上 24 + 2N字节（用于包含字符的数组），总共为 56 + 2N字节。

根据上下文，我们可能会或不会递归地计算对象的内存引用。例如，我们会计算String对象中的char[]数组的内存，因为这段内存是在创建字符串时分配的。但是，我们通常不会计算StackOfStrings对象中String对象的内存，因为这些String对象是由客户端创建的。

问与答

问. 如何增加 Java 分配的内存和堆栈空间？

A. 你可以通过使用 java -Xmx200m Hello 来增加分配给 Java 的内存量，其中 200m 表示 200 兆字节。默认设置通常为 64MB。你可以通过使用 java -Xss200k Hello 来增加分配给 Java 的堆栈空间量，其中 200k 表示 200 千字节。默认设置通常为 128KB。你可以通过使用 java -Xmx200m -Xss200k Hello 来同时增加内存和堆栈空间的量。

Q. 填充的目的是什么？

A. 填充使所有对象占用的空间是 8 字节的倍数。这可能会浪费一些内存，但可以加快内存访问和垃圾回收速度。

Q. 我在我的计算实验中得到了不一致的时间信息。有什么建议吗？

A. 确保你的计算消耗足够的 CPU 周期，以便你可以准确地测量它。通常，1 秒到 1 分钟是合理的。如果你使用了大量内存，那可能是瓶颈。考虑关闭 HotSpot 编译器，使用 java -Xint，以确保更统一的测试环境。缺点是你不再准确地测量你想要测量的内容，即实际运行时间。

Q. 如果考虑垃圾回收和其他运行时进程，链表实现的栈或队列是否真的保证每次操作的常数时间？

A. 我们的分析没有考虑许多系统效应（如缓存、垃圾回收和即时编译）-在实践中，这些效应很重要。特别是，默认的 Java 垃圾收集器仅保证每次操作的摊销常数时间。然而，有实时垃圾收集器保证最坏情况下每次操作的常数时间。实时 Java提供了 Java 的扩展，为各种运行时进程（如垃圾回收、类加载、即时编译和线程调度）提供最坏情况下的性能保证。

练习

给出以下代码片段的运行时间的增长顺序（作为 N 的函数）：

int sum = 0;
for (int n = N; n > 0; n /= 2)for (int i = 0; i < n; i++) sum++;

int sum = 0;
for (int i = 1; i < N; i *= 2)for(int j = 0; j < i; j++)sum++;

```
int sum = 0;
for (int i = 1; i < N; i *= 2)for (int j = 0; j < N; j++)sum++;
```
答案：线性（N + N/2 + N/4 + …）；线性（1 + 2 + 4 + 8 + …）；线性对数级（外部循环循环 lg N 次）。

创意问题

4-求和。 对 FourSum.java 问题开发一个蛮力解决方案。
数组中的局部最小值。 编写一个程序，给定一个由 n 个不同整数组成的数组 a[]，找到一个局部最小值：一个索引 i，使得a[i] < a[i-1] 和 a[i] < a[i+1]（假设相邻条目在范围内）。在最坏情况下，你的程序应该使用 ~ 2 lg n 次比较。

答案：检查中间值 a[n/2] 及其两个邻居 a[n/2 - 1] 和 a[n/2 + 1]。如果 a[n/2] 是局部最小值，则停止；否则在较小邻居的一半中搜索。
矩阵中的局部最小值。 给定一个由 n² 个不同整数组成的 n×n 数组 a[]，设计一个算法，其运行时间与 n log n 成正比，以找到一个局部最小值：一对索引 i 和 j，使得 a[i][j] < a[i+1][j]，a[i][j] < a[i][j+1]，a[i][j] < a[i-1][j]，以及 a[i][j] < a[i][j-1]（假设相邻条目在范围内）。

提示：找到第 n/2 行中的最小条目，称为 a[n/2][j]。如果它是局部最小值，则返回它。否则，检查它的两个垂直邻居 a[n/2-1][j] 和 a[n/2+1][j]。在较小邻居的一半中进行递归。

额外奖励：设计一个算法，其运行时间与 n 成正比。
双峰搜索。 如果一个数组由一个递增的整数序列紧接着一个递减的整数序列组成，则该数组是双峰的。编写一个程序，给定一个由 n 个不同 int 值组成的双峰数组，确定给定的整数是否在数组中。在最坏情况下，你的程序应该使用 ~ 3 log n 次比较。

答案: 使用二分查找的一个版本，如 BitonicMax.java 中所示，找到最大值（在~ 1 lg n次比较中）；然后使用二分查找在每个片段中搜索（每个片段在~ 1 lg n次比较中）。
只使用加法和减法的二分查找。 [Mihai Patrascu] 编写一个程序，给定一个按升序排列的包含n个不同整数的数组，确定给定的整数是否在数组中。你只能使用加法和减法以及恒定数量的额外内存。你的程序在最坏情况下的运行时间应与 log n成比例。

答案: 不要基于二的幂（二分查找）进行搜索，而是使用斐波那契数（也呈指数增长）。保持当前搜索范围为[i, i + F(k)]，并将 F(k)、F(k-1)保存在两个变量中。在每一步中，通过减法计算 F(k-2)，检查元素 i + F(k-2)，并将范围更新为[i, i + F(k-2)]或[i + F(k-2), i + F(k-2) + F(k-1)]。
带有重复项的二分查找。 修改二分查找，使其始终返回与搜索键匹配的项的键的最小（最大）索引。
从建筑物上扔鸡蛋。 假设你有一座N层的建筑物和大量的鸡蛋。假设如果鸡蛋从第F层或更高处扔下，就会摔碎，否则不会。首先，设计一种策略来确定F的值，使得在使用*~ lg N次扔鸡蛋时破碎的鸡蛋数量为~ lg N*，然后找到一种方法将成本降低到*~ 2 lg F*，当N远大于F时。

提示: 二分查找；重复加倍和二分查找。
从建筑物上扔两个鸡蛋。 考虑前面的问题，但现在假设你只有两个鸡蛋，你的成本模型是扔鸡蛋的次数。设计一种策略，确定F，使得扔鸡蛋的次数最多为 2 sqrt(√ N)，然后找到一种方法将成本降低到*~c √ F*，其中 c 是一个常数。

第一部分的解决方案: 为了达到 2 * sqrt(N)，在 sqrt(N)、2 * sqrt(N)、3 * sqrt(N)、…、sqrt(N) * sqrt(N)层放置鸡蛋。（为简单起见，我们假设 sqrt(N)是一个整数。）假设鸡蛋在第 k * sqrt(N)层摔碎。用第二个鸡蛋，你应该在区间(k-1) * sqrt(N)到 k * sqrt(N)中进行线性搜索。总共，你最多需要进行 2 * sqrt(N)次试验就能找到楼层 F。

第二部分的提示: 1 + 2 + 3 + … k ~ 1/2 k²。
热还是冷。 你的目标是猜测一个介于 1 和N之间的秘密整数。你反复猜测介于 1 和N之间的整数。每次猜测后，你会得知它是否等于秘密整数（游戏停止）；否则（从第二次猜测开始），你会得知猜测是更热（更接近）还是更冷（距离更远）比你之前的猜测。设计一个算法，在*~ 2 lg N次猜测中找到秘密数字。然后，设计一个算法，在~ 1 lg N*次猜测中找到秘密数字。

提示: 第一部分使用二分查找。对于第二部分，首先设计一个算法，在*~1 lg N次猜测中解决问题，假设你被允许在范围-N到 2N*中猜测整数。

网页练习

设 f 是一个单调递增的函数，满足 f(0) < 0 且 f(N) > 0。找到最小的整数 i，使得 f(i) > 0。设计一个算法，使得对 f()的调用次数为 O(log N)。
上下取整。 给定一组可比较的元素，x 的上取整是集合中大于或等于 x 的最小元素，下取整是小于或等于 x 的最大元素。假设你有一个按升序排列的包含 N 个项的数组。给出一个 O(log N)的算法，找到 x 的上取整和下取整。
使用 lg N 两路比较进行排名。 实现rank()，使其使用~ 1 lg N 两路比较（而不是~ 1 lg N 三路比较）。
身份。 给定一个按升序排列的包含 N 个不同整数（正数或负数）的数组 a。设计一个算法来找到一个索引 i，使得 a[i] = i，如果这样的索引存在的话。提示：二分查找。
多数派。 给定一个包含 N 个字符串的数组。如果一个元素出现次数超过 N/2 次，则称其为多数派。设计一个算法来识别多数派是否存在。你的算法应在线性对数时间内运行。
多数派。 重复上一个练习，但这次你的算法应在线性时间内运��，并且只使用恒定数量的额外空间。此外，你只能比较元素是否相等，而不能比较字典顺序。

答案：如果 a 和 b 是两个元素且 a != b，则移除它们两个；多数派仍然存在。使用 N-1 次比较找到多数派的候选者；使用 N-1 次比较检查候选者是否真的是多数派。
第二小元素。 给出一个算法，使用最少的比较次数从 N 个项目的列表中找到最小和第二小的元素。答案：通过构建一个锦标赛树，在 ceil(N + lg(N) - 2) 次比较中完成。每个父节点都是其两个子节点中的最小值。最小值最终在根节点处；第二小值在根节点到最小值的路径上。
查找重复项。 给定一个包含 N 个元素的数组，其中每个元素是介于 1 和 N 之间的整数，请编写一个算法来确定是否存在任何重复项。你的算法应在线性时间内运行，并使用 O(1) 额外空间。提示：你可以破坏数组。
查找重复项。 给定一个包含 N+1 个元素的数组，其中每个元素是介于 1 和 N 之间的整数，请编写一个算法来查找重复项。你的算法应在线性时间内运行，使用 O(1) 额外空间，并且不得修改原始数组。提示：指针加倍。
查找共同元素。 给定两个包含 N 个 64 位整数的数组，设计一个算法来打印出两个列表中都出现的所有元素。输出应按排序顺序排列。你的算法应在 N log N 时间内运行。提示：归并排序，归并排序，合并。备注：在基于比较的模型中，不可能比 N log N 更好。
查找共同元素。 重复上述练习，但假设第一个数组有 M 个整数，第二个数组有 N 个整数，其中 M 远小于 N。给出一个在 N log M 时间内运行的算法。提示：排序和二分查找。
变位词。 设计一个 O(N log N) 算法来读取一个单词列表，并打印出所有的变位词。例如，字符串 “comedian” 和 “demoniac” 是彼此的变位词。假设有 N 个单词，每个单词最多包含 20 个字母。设计一个 O(N²) 的算法应该不难，但将其降至 O(N log N) 需要一些巧妙的方法。
在排序、旋转数组中搜索。 给定一个包含 n 个不同整数的排序数组，该数组已经旋转了未知数量的位置，例如，15 36 1 7 12 13 14，请编写一个程序 RotatedSortedArray.java 来确定给定的整数是否在列表中。你的算法的运行时间增长应为对数级别。
找到数组中的跳跃。 给定一个由 n 个整数组成的数组，形式为 1, 2, 3, …, k-1, k+j, k+j+1, …, n+j，其中 1 <= k <= n 且 j > 0，请设计一个对数时间算法来找到整数 k。也就是说，数组包含整数 1 到 n，只是在某个点上，所有剩余值都增加了 j。
找到缺失的整数。 一个数组 a[] 包含从 0 到 N 的所有整数，除了 1。但是，你不能通过单个操作访问一个元素。相反，你可以调用 get(i, k)，它返回 a[i] 的第 k 位，或者你可以调用 swap(i, j)，它交换 a[] 的第 i 和第 j 个元素。设计一个 O(N) 算法来找到缺失的整数。为简单起见，假设 N 是 2 的幂。
最长的 0 行。 给定一个由 0 和 1 组成的 N×N 矩阵，使得在每行中 0 不会出现在 1 之前，找到具有最多 0 的行，并在 O(N) 时间内完成。
单调二维数组。 给定一个 n×n 的元素数组，使得每行按升序排列，每列也按升序排列，设计一个 O(n)的算法来确定数组中是否存在给定元素 x。你可以假设 n×n 数组中的所有元素都是不同的。
你站在一条路中间，但有一场尘暴遮挡了你的视线和方向。只有一个方向有庇护所，但直到你站在它面前才能看到任何东西。设计一个能够找到庇护所的算法，保证能找到。你的目标是尽量减少步行的距离。提示：某种来回走动的策略。
通过尽可能大的常数因子改进以下代码片段，以适应大规模 n。通过性能分析确定瓶颈在哪里。假设b[]是一个长度为n的整数数组。
```
double[] a = new double[n];
for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)a[j] += Math.exp(-0.5 * (Math.pow(b[i] - b[j], 2)); 
```
原地置换。 编写一个程序Permutation.java，其中包含接受数组和置换（或逆置换）的函数，并根据置换（或逆置换）重新排列数组中的元素。原地操作：只使用恒定量的额外内存。
三数之和。 给定三个集合 A、B 和 C，每个集合最多包含 N 个整数，确定是否存在三元组 a 在 A 中，b 在 B 中，c 在 C 中，使得 a + b + c = 0。

答案：按升序对 B 进行排序；按降序对 C 进行排序；对于 A 中的每��a，扫描 B 和 C，找到一个对，使得它们的和为-a（当和太小时，在 B 中前进，当和太大时，在 C 中前进）。
两数之和。 给定两个集合 A 和 B，每个集合最多包含 N 个整数，确定 A 中任意两个不同整数的和是否等于 B 中的一个整数。
连续和。 给定一组实数和目标值 V，找到一个连续块（任意长度），其和尽可能接近 V。

暴力法：通过暴力法计算每个连续块的总和。这需要 O(N³)的时间。

部分和：计算所有部分和 s[i] = a[0] + a[1] + … + a[i]，以便连续块的和形式为 s[j] - s[i]。这需要 O(N²)的时间。

排序和二分查找：按上述方式形成部分和，然后按升序对它们进行排序。对于每个 i，二分查找尽可能接近 s[i]的 s[j]。这需要 O(N log N)的时间。
三变量的线性方程。 对于三个变量的固定线性方程（例如整数系数），给定 N 个数字，其中任意三个是否满足方程？为该问题设计一个二次算法。提示：参见三数之和的二次算法。
卷积三数之和。 给定 N 个实数，确定是否存在索引 i 和 j，使得 a[i] + a[j] = a[i+j]。为该问题设计一个二次算法。提示：参见三数之和的二次算法。
找到主要项。 给定一个从标准输入中任意长的项序列，其中一个项出现的次数严格占多数，识别主要项。只使用恒定量的内存。

解决方案。 维护一个整数计数器和一个变量来存储当前的冠军项。读取下一个项，如果该项等于冠军项，则将计数器加一。(ii) 否则将计数器减一，如果计数器达到 0，则用当前项替换冠军值。终止时，冠军值将是主要项。
数组的记忆。 MemoryOfArrays.java。依赖于 LinearRegression.java。
字符串和子字符串的记忆。 MemoryOfStrings.java。依赖于 LinearRegression.java 和 PolynomialRegression.java。取决于你使用的是 Java 6 还是 Java 7。
栈和队列的记忆。 作为 N 个项的栈的内存使用量是 N 的函数吗？

解决方案。 32 + 40N（不包括引用对象的内存）。MemoryOfStacks.java。
欧几里得算法的分析。 证明欧几里得算法的时间复杂度最多与N成正比，其中N是较大输入中的位数。

答案：首先我们假设 p > q。如果不是，则第一个递归调用实际上会交换 p 和 q。现在，我们要证明在至多 2 次递归调用后，p 会减少一半。为了证明这一点，有两种情况需要考虑。如果 q ≤ p / 2，则下一个递归调用将有 p’ = q ≤ p / 2，因此在仅一次递归调用后，p 至少减少了一半。否则，如果 p / 2 < q < p，则 q’ = p % q = p - q < p / 2，因此 p’’ = q’ < p / 2，经过两次迭代后，p 将减少一半或更多。因此，如果 p 有 N 位，则在至多 2N 次递归调用后，欧几里得算法将达到基本情况。因此，总步数与 N 成正比。
查找重复项。 给定一个包含 0 到 N 之间的 N+2 个整数的排序数组，其中恰好有一个重复项，设计一个对数时间复杂度的算法来找到重复项。

提示二分查找。

给定一个包含 n 个实数的数组a[]，设计一个线性时间算法来找到a[j] - a[i]的最大值，其中j ≥ i。

解决方案：

double best = 0.0;
double min = a[0];
for (int i = 0; i < n; i++) {min  = Math.min(a[i], min);best = Math.max(a[i] - min, best);
}

给定一个包含 n 个实数的数组a[]，设计一个线性时间算法来找到|a[j] - a[i]| + |j - i|的最大值。

提示：创建两个长度为 n 的数组 b[]和 c[]，其中 b[i] = a[i] - i，c[i] = a[i] + i。

1.5 案例研究：并查集

原文：algs4.cs.princeton.edu/15uf

译者：飞龙

协议：CC BY-NC-SA 4.0

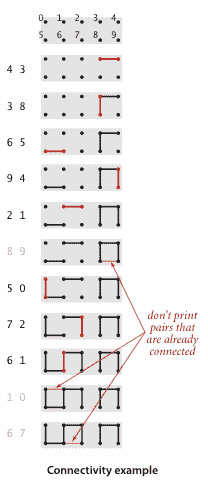
动态连通性示例

动态连通性。

输入是一系列整数对，其中每个整数表示某种类型的对象，我们将解释对p q为p连接到q。我们假设“连接到”是一个等价关系：

对称性：如果p连接到q，那么q连接到p。
传递性：如果p连接到q且q连接到r，那么p连接到r。
自反性：p连接到p。

等价关系将对象划分为等价类或连通分量。

我们的目标是编写一个程序来过滤序列中的多余对：当程序从输入中读取一对p q时，只有当它到目前为止看到的对不意味着p连接到q时，它才将这对写入输出。如果之前的对确实意味着p连接到q，那么程序应忽略这对p q并继续读取下一对。

并查集 API。

以下 API 封装了我们需要的基本操作。并查集 API

为了测试 API 的实用性，UF.java 中的main()解决了动态连通性问题。我们还准备了测试数据：文件 tinyUF.txt 包含我们小例子中使用的 11 个连接，文件 mediumUF.txt 包含 900 个连接，文件 largeUF.txt 是一个包含数百万连接的示例。

实现。

我们现在考虑几种不同的实现方式，都基于使用一个站点索引数组id[]来确定两个站点是否在同一个组件中。

快速查找. QuickFindUF.java 维护了这样一个不变量：当且仅当id[p]等于id[q]时，p和q连接。换句话说，组件中的所有站点在id[]中必须具有相同的值。
快速联合. QuickUnionUF.java 基于相同的数据结构——站点索引id[]数组，但它使用了不同的值解释，导致更复杂的结构。具体来说，每个站点的id[]条目将是同一组件中另一个站点的名称（可能是它自己）。为了实现find()，我们从给定站点开始，沿着它的链接到另一个站点，再沿着那个站点的链接到另一个站点，依此类推，一直沿着链接直到到达一个根节点，一个有链接指向自身的站点。只有当这个过程将它们导向相同的根节点时，两个站点才在同一个组件中。为了验证这个过程，我们需要union()来维护这个不变量，这很容易安排：我们沿着链接找到与每个给定站点相关联的根节点，然后通过将其中一个根节点链接到另一个根节点来重命名一个组件。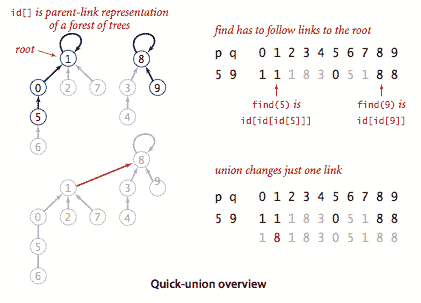
加权快速联合. 在快速联合算法中，为了union()将第二棵树任意连接到第一棵树，我们跟踪每棵树的大小，并始终将较小的树连接到较大的树。程序 WeightedQuickUnionUF.java 实现了这种方法。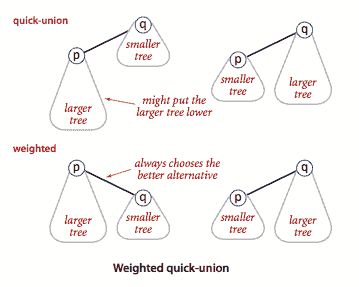
带路径压缩的加权快速联合. 有许多简单的方法可以进一步改进加权快速联合算法。理想情况下，我们希望每个节点直接链接到其树的根节点，但我们不想付出改变大量链接的代价。我们可以通过使我们直接检查的所有节点直接链接到根节点来接近理想状态。

并查集成本模型。

在研究并查集算法时，我们计算数组访问次数（访问数组条目的次数，用于读取或写入）。

定义。

树的大小是其节点数。树中节点的深度是从节点到根的路径上的链接数。树的高度是其节点中的最大深度。

命题。

快速查找算法对每次find()调用使用一个数组访问，并且对于每次将两个组件合并的union()调用，数组访问次数在n + 3 和 2n + 1 之间。

命题。

在快速联合中，find()所使用的数组访问次数为 1 加上节点深度的两倍，该节点对应给定站点。union()和connected()所使用的数组访问次数为两个find()操作的成本（如果给定站点在不同树中，则union()还需加 1）。

命题。

由加权快速联合构建的森林中任何节点的深度最多为 lg n。

推论。

对于具有n个站点的加权快速联合，find()、connected()和union()的最坏情况成本增长顺序为 log n。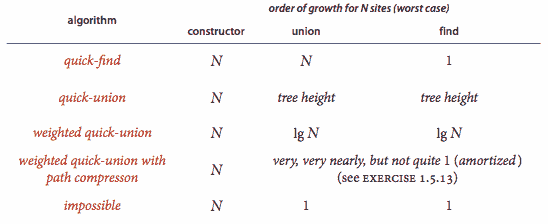 union-find 算法的性能

问与答

Q. 是否有一种有效的数据结构，支持边的插入和删除？

A. 是的。然而，用于图连接性的已知最佳完全动态数据结构比我们考虑的增量版本复杂得多。此外，它的效率也不如增量版本。参见 Mikkel Thorup 的Near-optimal fully-dynamic graph connectivity。

练习

开发类 QuickUnionUF.java 和 QuickFindUF.java，分别实现快速联合和快速查找。
给出一个反例，说明快速查找的union()的这种直观实现是不正确的：
```
public void union(int p, int q) {if (connected(p, q)) return;for (int i = 0; i < id.length; i++)if (id[i] == id[p]) id[i] = id[q];count--;
}
```
答案. 在 for 循环中，id[p]的值会改变为id[q]。因此，任何r > p且id[r]等于id[p]的对象都不会被更新为等于id[q]。
在加权快速联合实现中，假设我们将id[root(p)]设置为q而不是id[root(q)]。得到的算法是否正确？

答案. 是的。然而，这会增加树的高度，因此性能保证将无效。

创意问题

带路径压缩的快速联合。 修改 QuickUnionUF.java 以包括路径压缩，通过在find()中添加一个循环，将从 p 到根的路径上的每个站点连接起来。给出一系列输入对，使得该方法产生长度为 4 的路径。注意：该算法的摊销成本每次操作已知为对数级别。

解决方案. QuickUnionPathCompressionUF.java。
带路径压缩的加权快速联合。 修改 WeightedQuickUnionUF.java 以实现路径压缩，如练习 1.5.12 所述。给出一系列输入对，使得该方法产生高度为 4 的树。

注意：该算法的摊销成本每次操作已知受到称为反阿克曼函数的函数的限制，对于实践中出现的任何可想象的n值，该函数均小于 5。

解决方案. WeightedQuickUnionPathCompressionUF.java。
按高度加权快速联合。 开发一个实现 WeightedQuickUnionByHeightUF.java 的算法，该算法使用与加权快速联合相同的基本策略，但跟踪树高度并始终将较短的树链接到较高的树。证明对于n个站点，您的算法对树的高度有对数上界。

解决方案. 不同树中元素之间的联合操作要么保持高度不变（如果两棵树的高度不同），要么增加一次高度（如果两棵树的高度相同）。你可以通过归纳证明树的大小至少为 2^高度。因此，高度最多可以增加 lg n次。
随机连接。开发一个UF客户端 ErdosRenyi.java，接受一个整数命令行参数n��在 0 到n之间生成随机整数对，调用connected()确定它们是否连接，如果没有连接则调用union()（与我们的开发客户端相同），循环直到所有站点连接，并打印生成的连接数。将程序打包为一个以n为参数的静态方法count()，返回连接数和一个从命令行获取n的main()，调用count()，并打印返回的值。

网页练习

真或假。在快速联合实现中，假设我们将parent[p]设置为parent[root(q)]而不是将parent[root(p)]设置为parent[root(q)]，得到的算法是否正确？

答案。不。
在执行带路径压缩的加权快速联合时，以下哪个数组不可能出现：
1. 0 1 2 3 4 5 6 7 8 9
2. 7 3 8 3 4 5 6 8 8 1
3. 6 3 8 0 4 5 6 9 8 1
4. 0 0 0 0 0 0 0 0 0 0
5. 9 6 2 6 1 4 5 8 8 9
6. 9 8 7 6 5 4 3 2 1 0
解决方案。B、C、E 和 F。

递归路径压缩。使用递归实现路径压缩。

解决方案：

public int find(int p) {if (p != parent[p])parent[p] = find(parent[p]);return parent[p];

路径减半。编写一个数据类型 QuickUnionPathHalvingUF.java，实现一种更简单的策略，称为路径减半，使得查找路径上的每个其他节点都链接到其祖父节点。备注：该算法每次操作的摊销成本被限制在一个称为反阿克曼函数的函数中。
路径分裂。编写一个数据类型 WeightedQuickUnionPathSplittingUF.java，实现一种称为路径分裂的替代策略，使得查找路径上的每个节点都链接到其祖父节点。备注：该算法每次操作的摊销成本被限制在一个称为反阿克曼函数的函数中。
随机快速联合。实现以下版本的快速联合：将整数 0 到 n-1 均匀随机分配给 n 个元素。在链接两个根时，始终将具有较小标签的根链接到具有较大标签的根。添加路径压缩。备注：没有路径压缩版本的每次操作的期望成本是对数级的；具有路径压缩版本的每次操作的期望摊销成本被限制在一个称为反阿克曼函数的函数中。
3D 位置渗透。对 3D 晶格重复。阈值约为 0.3117。
键合渗透。与位置渗透相同，但是随机选择边而不是位置。真实阈值恰好为 0.5。
给定一组 N 个元素，创建一个 N 个联合操作的序列，使得带权重的快速联合的高度为 Theta(log N)。对带路径压缩的带权重快速联合重复。
六角形。六角形游戏在一个梯形六边形网格上进行…描述如何检测白色或黑色何时赢得游戏。使用并查集数据结构。
六角形。证明游戏不可能以平局结束。提示：考虑从棋盘左侧可达的单元格集合。
六角形。证明第一个玩家可以通过完美的游戏获胜。提示：如果第二个玩家有一个获胜策略，你可以最初选择一个随机单元格，然后只需复制第二个玩家的获胜策略。这被称为策略窃取。
在网格上标记聚类。 物理学家将其称为Hoshen–Kopelman 算法，尽管它只是在栅格图上进行的并查集算法，按照栅格扫描顺序进行。应用包括模拟渗透和电导。绘制站点占用概率与聚类数量的关系（比如 100x100，p 在 0 到 1 之间，聚类数量在 0 到 1500 之间）或聚类分布。（似乎 DFS 在这里就足够了）Matlab 在图像处理工具箱中有一个名为bwlabel的函数，用于执行聚类标记。

2. 排序

原文：algs4.cs.princeton.edu/20sorting

译者：飞龙

协议：CC BY-NC-SA 4.0

概述。

排序是重新排列一系列对象的过程，使它们按照某种逻辑顺序排列。排序在商业数据处理和现代科学计算中起着重要作用。在交易处理、组合优化、天体物理学、分子动力学、语言学、基因组学、天气预测等领域都有广泛的应用。

在本章中，我们考虑了几种经典的排序方法以及一个称为优先队列的基本数据类型的高效实现。我们讨论了比较排序算法的理论基础，并以对排序和优先队列算法的应用进行调查来结束本章。

2.1 Elementary Sorts介绍了选择排序、插入排序和希尔排序。
2.2 Mergesort描述了归并排序，这是一种能够保证在线性对数时间内运行的排序算法。
2.3 Quicksort描述了快速排序，它比其他任何排序算法都被广泛使用。
2.4 Priority Queues介绍了优先队列数据类型以及使用二叉堆的高效实现。它还介绍了堆排序。
2.5 Applications描述了排序的应用，包括使用替代排序、选择、系统排序和稳定性。

本章的 Java 程序。

以下是本章中的 Java 程序列表。点击程序名称以访问 Java 代码；点击参考号以获取简要描述；阅读教材以获取全面讨论。

REF PROGRAM DESCRIPTION / JAVADOC
2.1 Insertion.java 插入排序
- InsertionX.java 插入排序（优化版）
- BinaryInsertion.java 二分插入排序
2.2 Selection.java 选择排序
2.3 Shell.java 希尔排序
2.4 Merge.java 自顶向下的归并排序
- MergeBU.java 自底向上的归并排序
- MergeX.java 优化的归并排序
- Inversions.java 逆序对数量
2.5 Quick.java 快速排序
- Quick3way.java 三向切分的快速排序
- QuickX.java 优化的双向快速排序
- QuickBentleyMcIlroy.java 优化的三向快速排序
- TopM.java 优先队列客户端
2.6 MaxPQ.java 最大堆优先队列
- MinPQ.java 最小堆优先队列
- IndexMinPQ.java 索引最小堆优先队列
- IndexMaxPQ.java 索引最大堆优先队列
- Multiway.java 多路归并
2.7 Heap.java 堆排序

REF	PROGRAM	DESCRIPTION / JAVADOC
2.1	Insertion.java	插入排序
-	InsertionX.java	插入排序（优化版）
-	BinaryInsertion.java	二分插入排序
2.2	Selection.java	选择排序
2.3	Shell.java	希尔排序
2.4	Merge.java	自顶向下的归并排序
-	MergeBU.java	自底向上的归并排序
-	MergeX.java	优化的归并排序
-	Inversions.java	逆序对数量
2.5	Quick.java	快速排序
-	Quick3way.java	三向切分的快速排序
-	QuickX.java	优化的双向快速排序
-	QuickBentleyMcIlroy.java	优化的三向快速排序
-	TopM.java	优先队列客户端
2.6	MaxPQ.java	最大堆优先队列
-	MinPQ.java	最小堆优先队列
-	IndexMinPQ.java	索引最小堆优先队列
-	IndexMaxPQ.java	索引最大堆优先队列
-	Multiway.java	多路归并
2.7	Heap.java	堆排序

排序演示。

以下是一些有趣的排序演示。

排序算法动画，作者 David Martin。
排序算法的声音和可视化，作者 Timo Bingmann。
快速排序的声音。
机器人可视化展示快速排序和归并排序。
Carlo Zapponi 的排序可视化，使用逆序计数作为进度的衡量标准。

2.1 基本排序

原文：algs4.cs.princeton.edu/21elementary

译者：飞龙

协议：CC BY-NC-SA 4.0

在本节中，我们将学习两种基本的排序方法（选择排序和插入排序）以及其中一种的变体（希尔排序）。

游戏规则。

我们的主要关注点是重新排列包含关键字的项目数组的算法，目标是重新排列项目，使它们的关键字按升序排列。在 Java 中，关键字的抽象概念在内置机制中��现为Comparable接口。除了少数例外，我们的排序代码只通过两个操作引用数据：比较对象的方法less()和交换它们的方法exch()。

private static boolean less(Comparable v, Comparable w) {return (v.compareTo(w) < 0);
}private static void exch(Comparable[] a, int i, int j) {Comparable swap = a[i];a[i] = a[j];a[j] = swap;
}

排序成本模型。在研究排序算法时，我们计算比较和交换。对于不使用交换的算法，我们计算数组访问。
额外内存。我们考虑的排序算法分为两种基本类型：一种是原地排序（除了可能需要一小段函数调用堆栈或常数数量的实例变量外，不需要额外内存），另一种是需要足够额外内存来保存另一个要排序的数组的副本。
数据类型。我们的排序代码适用于实现 Java 的Comparable 接口的任何数据类型。这意味着存在一个compareTo()方法，其中v.compareTo(w)在 v < w 时返回负整数，在 v = w 时返回零，在 v > w 时返回正整数。该方法必须实现全序：
- *自反性：*对于所有的 v，v = v。
- *反对称性：*对于所有的 v 和 w，如果(v < w)，那么(w > v)；如果(v = w)，那么(w = v)。
- *传递性：*对于所有的 v、w 和 x，如果(v ≤ w)且(w ≤ x)，那么 v ≤ x。
此外，如果v和w是不兼容类型或其中任何一个为null，v.compareTo(w)必须抛出异常。

Date.java 演示了如何为用户定义的类型实现Comparable接口。

选择排序。

最简单的排序算法之一的工作方式如下：首先，在数组中找到最小的项，并将其与第一个条目交换。然后，找到下一个最小的项并将其与第二个条目交换。继续这样做，直到整个数组排序完成。这种方法被称为选择排序，因为它通过重复选择剩余的最小项来工作。Selection.java 是这种方法的实现。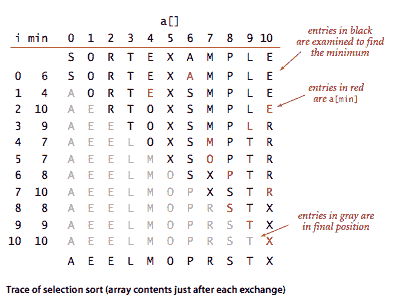

命题。

选择排序使用~n²/2 次比较和 n 次交换来对长度为 n 的数组进行排序。

插入排序。

人们经常用来排序桥牌的算法是逐个考虑卡片，将每张卡片插入到已考虑的卡片中的适当位置（保持它们排序）。在计算机实现中，我们需要为当前项目腾出空间，通过将较大的项目向右移动一个位置，然后将当前项目插入到空出的位置。Insertion.java 是这种方法的实现，称为插入排序。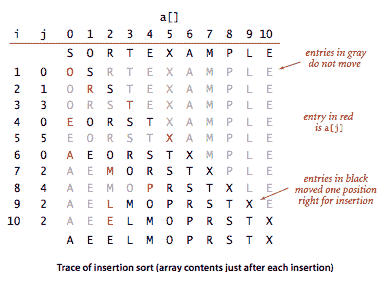选择排序

命题。

对于具有不同键的长度为 N 的随机排序数组，插入排序平均使用~N²/4 次比较和~N²/4 次交换。最坏情况下，使用~N²/2 次比较和~N²/2 次交换，最佳情况下是 N-1 次比较和 0 次交换。

插入排序对于某些在实践中经常出现的非随机数组非常有效，即使它们很大。逆序对是数组中顺序不正确的一对关键字。例如，E X A M P L E 有 11 个逆序对：E-A、X-A、X-M、X-P、X-L、X-E、M-L、M-E、P-L、P-E 和 L-E。如果数组中的逆序对数量小于数组大小的常数倍，则称该数组是部分排序的。

命题。

插入排序使用的交换次数等于数组中的逆序数，比较次数至少等于逆序数，最多等于逆序数加上数组大小。

属性。

对于具有不同值的随机排序数组，插入排序和选择排序的运行时间是二次的，并且彼此之间相差一个小的常数因子。

SortCompare.java 使用命令行参数中命名的类中的sort()方法执行给定数量的实验（对给定大小的数组进行排序），并打印算法观察运行时间的比率。

可视化排序算法。

我们使用简单的可视化表示来描述排序算法的属性。我们使用垂直条形图，按其高度排序。SelectionBars.java 和 InsertionBars.java 生成这些可视化效果。选择排序和插入排序的可视化效果

希尔排序。

希尔排序是插入排序的简单扩展，通过允许远离的条目进行交换，以产生部分排序的数组，最终可以通过插入排序高效地排序。其思想是重新排列数组，使其具有这样的属性：取每个第 h 个条目（从任何位置开始）会产生一个排序序列。这样的数组称为h-排序。通过对一些大的 h 值进行 h-排序，我们可以将数组中的条目移动到较远的距离，从而使得对较小的 h 值进行 h-排序更容易。对于以 1 结尾的任何增量序列的值使用这种过程将产生一个排序的数组：这就是希尔排序。Shell.java 是这种方法的实现。

ShellBars.java 生成希尔排序的可视化效果。

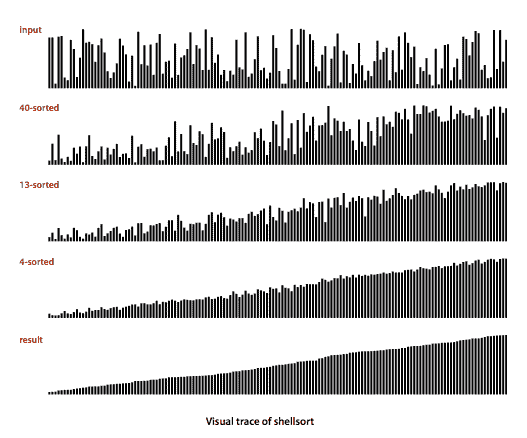
希尔排序的可视化效果

属性。

使用增量为 1、4、13、40、121、364 的希尔排序所使用的比较次数受到 N 的倍数限制，与使用的增量数量成正比。

命题。

使用增量为 1、4、13、40、121、364 的希尔排序所使用的比较次数为 O(N^(3/2))。

问与答

Q. 当我编译 Insertion.java 时，编译器会发出警告。有没有办法避免这种情况？

Insertion.java:73: warning: [unchecked] unchecked call to compareTo(T)as a member of the raw type java.lang.Comparablereturn (v.compareTo(w) < 0);

A. 是的，如果使用静态泛型，就像 InsertionPedantic.java 一样。这会导致笨拙（但无警告）的代码。

练习

以选择排序示例跟踪的方式展示选择排序如何对数组进行排序。
```
E A S Y Q U E S T I O N
```
解决方案。
在选择排序中涉及任何特定项目的最大交换次数是多少？涉及特定项目 x 的平均交换次数是多少？

解决方案。 平均交换次数恰好为 2，因为总共有 n 次交换和 n 个项目（每次交换涉及两个项目）。最大交换次数为 n，如下例所示。
以插入排序示例跟踪的方式展示插入排序如何对数组进行排序。
```
E A S Y Q U E S T I O N
```
解决方案。
对于所有键相同的数组，选择排序和插入排序哪个运行速度更快？

解决方案。 当所有键相等时，插入排序运行时间为线性时间。
假设我们在一个随机排序的数组上使用插入排序，其中项目只有三个键值之一。运行时间是线性的、二次的还是介于两者之间的？

解决方案。 二次的。
以希尔排序示例跟踪的方式展示希尔排序如何对数组进行排序。
```
E A S Y S H E L L S O R T Q U E S T I O N
```
解决方案。
为什么在希尔排序的h排序中不使用选择排序？

解决方案。 插入排序在部分排序的输入上更快。

创意问题

昂贵的交换。 一家运输公司的职员负责按照要运出的时间顺序重新排列一些大箱子。因此，相对于交换的成本（移动箱子），比较的成本非常低（只需查看标签）。仓库几乎满了：有足够的额外空间来容纳任何一个箱子，但不能容纳两个。职员应该使用哪种排序方法？

解决方案。 使用选择排序，因为它最小化了交换的次数。
可视化跟踪。 修改你对上一个练习的解决方案，使 Insertion.java 和 Selection.java 产生类似本节中所示的可视化跟踪。

解决方案。 TraceInsertion.java、TraceSelection.java 和 TraceShell.java。
可比较的交易。 扩展你的 Transaction.java 实现，使其实现Comparable，使得交易按金额顺序排列。
交易排序测试客户端。 编写一个类 SortTransactions.java，其中包含一个静态方法main()，从标准输入读取一系列交易，对其进行排序，并在标准输出上打印结果。

实验

带哨兵的插入排序。 开发一个插入排序的实现 InsertionX.java，通过首先将最小的项目放入位置来消除内部循环中的 j > 0 测试。使用 SortCompare.java 来评估这样做的有效性。注意：通常可以通过这种方式避免索引越界测试——使测试能够被消除的项目称为哨兵。
无交换的插入排序。 开发一个插入排序的实现 InsertionX.java，将较大的项目向右移动一个位置，而不是进行完整的交换。使用 SortCompare.java 来评估这样做的有效性。

网络练习

排序网络。 编写一个程序 Sort3.java，其中有三个if语句（没有循环），从命令行读取三个整数a、b和c，并按升序打印它们。
```
if (a > b) swap a and b
if (a > c) swap a and c
if (b > c) swap b and c
```

无视排序网络。 说服自己，以下代码片段重新排列存储在变量 A、B、C 和 D 中的整数，使得 A <= B <= C <= D。

if (A > B) { t = A; A = B; B = t; }
if (B > C) { t = B; B = C; C = t; }
if (A > B) { t = A; A = B; B = t; }
if (C > D) { t = C; C = D; D = t; }
if (B > C) { t = B; B = C; C = t; }
if (A > B) { t = A; A = B; B = t; }
if (D > E) { t = D; D = E; E = t; }
if (C > D) { t = C; C = D; D = t; }
if (B > C) { t = B; B = C; C = t; }
if (A > B) { t = A; A = B; B = t; }

设计一系列语句，可以对 5 个整数��行排序。你的程序使用了多少个if语句？

最佳的无视排序网络。 创建一个程序，使用仅 5 个if语句对四个整数进行排序，以及使用仅 9 个上述类型的if语句对五个整数进行排序？无视排序网络对于在硬件中实现排序算法很有用。如何检查你的程序对所有输入都有效？

答案： Sort4.java 使用 5 个比较交换对 4 个项目进行排序。Sort5.java 使用 9 个比较交换对 5 个项目进行排序。

0-1 原则说，你可以通过检查一个（确定性的）排序网络是否正确地对由 0 和 1 组成的输入进行排序来验证其正确性。因此，要检查Sort5.java是否有效，你只需要在 32 个可能的由 0 和 1 组成的输入上测试它。
最佳的无视排序（具有挑战性）。 找到一个针对 6、7 和 8 个输入的最佳排序网络，分别使用 12、16 和 19 个上一个问题中形式的if语句。

答案：Sort6.java 是对 6 个项目进行排序的解决方案。
最佳非盲目排序。 编写一个程序，仅使用 7 次比较对 5 个输入进行排序。提示：首先比较前两个数字，然后比较后两个数字，以及两组中较大的数字，并标记它们，使得 a < b < d 和 c < d。其次，将剩余的项目 e 插入到链 a < b < d 中的适当位置，首先与 b 进行比较，然后根据结果与 a 或 d 进行比较。第三，以与插入 e 相同的方式将 c 插入到涉及 a、b、d 和 e 的链中的适当位置（知道 c < d）。这使用了 3（第一步）+ 2（第二步）+ 2（第三步）= 7 次比较。这种方法最初是由 H.B. Demuth 在 1956 年发现的。
Stupidsort。 分析以下排序算法的运行时间（最坏情况和最佳情况）、正确性和稳定性。从左到右扫描数组，直到找到两个连续的位置不正确的项。交换它们，并从头开始。重复直到扫描到数组的末尾。
```
for (int i = 1; i < N; i++) {if (less(a[i], a[i-1])) {exch(i, i-1);i = 0;}
}
```
考虑以下递归变体并分析最坏情况下的内存使用情况。
```
public static void sort(Comparable[] a) {for (int i = 1; i < a.length; i++) {if (less(a[i], a[i-1])) {exch(i, i-1);sort(a);}}
}
```
Stoogesort。 分析以下递归排序算法的运行时间和正确性：如果最左边的项大于最右边的项，则交换它们。如果当前子数组中有 2 个或更多项，(i) 递归地对数组的前两个三分之一进行排序，(ii) 对数组的最后两个三分之一进行排序，(iii) 再次对数组的前两个三分之一进行排序。
猜测排序。 随机选择两个索引 i 和 j；如果 a[i] > a[j]，则交换它们。重复直到输入排序。分析此算法的预期运行时间。提示：每次交换后，逆序的数量会严格减少。如果有 m 个坏对，那么找到一个坏对的预期时间为 Theta(n²/m)。从 m = 1 到 n² 求和得到 O(N² log N)的总体时间，类似于收集优惠券。这个界限是紧的：考虑输入 1 0 3 2 5 4 7 6 …
Bogosort。 Bogosort 是一种随机算法，通过将 N 张卡片抛起来，收集它们，并检查它们是否以递增顺序排列。如果没有，重复直到它们排好序。使用第 1.4 节中的洗牌算法实现 bogosort。估计运行时间作为 N 的函数。
慢速排序。 考虑以下排序算法：随机选择两个整数 i 和 j。如果 i < j，但 a[i] > a[j]，则交换它们。重复直到数组按升序排列。论证该算法最终会完成（概率为 1）。作为 N 的函数，它需要多长时间？提示：在最坏情况下，它会进行多少次交换？
对数组进行排序的最小移动次数。 给定一个包含 N 个键的列表，移动操作包括从列表中移除任意一个键并将其附加到列表的末尾。不允许其他操作。设计一个算法，使用最少的移动次数对给定列表进行排序。
猜测排序。 考虑以下基于交换的排序算法：随机选择两个索引；如果 a[i]和 a[j]是一个逆序，交换它们；重复。证明对大小为 N 的数组进行排序的预期时间最多为 N² log N。参见此论文进行分析，以及称为 Fun-Sort 的相关排序算法。
交换一个逆序。 给定一个包含 N 个键的数组，设 a[i]和 a[j]是一个逆序（i < j 但 a[i] > a[j]）。证明或证伪：交换 a[i]和 a[j]会严格减少逆序的数量。
二进制插入排序。 开发一个实现 BinaryInsertion.java 的插入排序，该排序使用二分查找来找到插入点 j 以便将条目 a[i]插入，然后将所有条目 a[j]到 a[i-1]向右移动一个位置。在最坏情况下，对长度为 n 的数组进行排序的比较次数应该约为~ n lg n。请注意，在最坏情况下，数组访问次数仍然是二次的。使用 SortCompare.java 来评估这样做的有效性。