如果图片本身比较小，卷积之后输出也会很小，那么可以在图片与卷积核相乘之前先填充一下，让输出为预期大小

一般填充后输入，输出相同

当图片比较大的时候，如果利用卷积核去得到我们想要的大小的话，得用到多层卷积核来，一步步得出我们期望的大小，这就导致卷积的层数很大，权重的数量变多，模型的大小也会变大

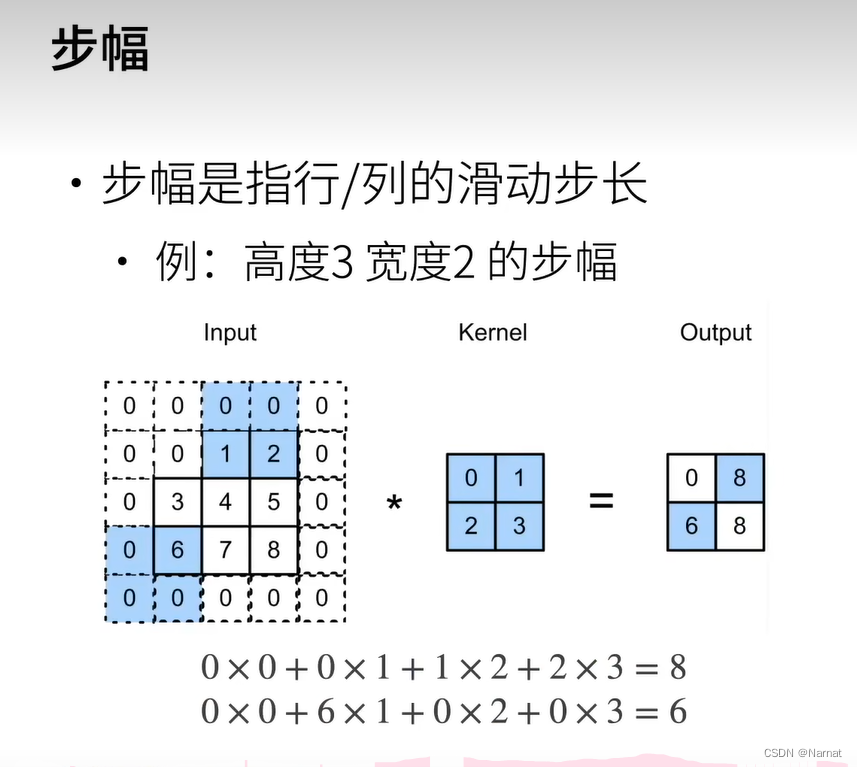
解决这个问题的方式，就是让卷积核能够每隔多个长度做一次扫描，这样一层卷积核一次的操作即可让输出变得很小

填充代码：

import torch
from torch import nn# 为了方便起见，我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):# 这里的（1，1）表示批量大小和通道数都是1X = X.reshape((1, 1) + X.shape)  # 填充两个维度Y = conv2d(X)# 省略前两个维度：批量大小和通道return Y.reshape(Y.shape[2:])# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)  #规定输入数据的通道数，输出数据的通道数，卷积核3*3，填充一圈0
X = torch.rand(size=(8, 8))  # 8 * 8 二维
print(comp_conv2d(conv2d, X).shape)

卷积模型输入需要四维张量，分别是样本数量，通道数，高度，宽度，其中通道数指的是图片的颜色灰色图片一个通道，彩色图片三个通道

原本这个模型的输出应该是（8 - 3 + 1）* （8 - 3 + 1）输出，但是由于在两边都填充了一边0所以填充后的输出是（8 + 2 - 3 + 1）*（8 + 2 -3 + 1）依旧是原本输出的形状

代码：

import torch
from torch import nn# 为了方便起见，我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):# 这里的（1，1）表示批量大小和通道数都是1X = X.reshape((1, 1) + X.shape)  # 填充两个维度Y = conv2d(X)# 省略前两个维度：批量大小和通道return Y.reshape(Y.shape[2:])# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
X = torch.rand(size=(8, 8))  # 8 * 8 二维
print(comp_conv2d(conv2d, X).shape)

不规则填充卷积核是5 * 3,那么输出大小原本是（8 - 5 + 1） * （8 - 3 + 1）但是上下填充1行，左右填充两列，最后输出是（8 - 5 + 4 + 1） * （8 - 3 + 2 + 1)依旧不变

代码：

import torch
from torch import nn# 为了方便起见，我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):# 这里的（1，1）表示批量大小和通道数都是1X = X.reshape((1, 1) + X.shape)  # 填充两个维度Y = conv2d(X)# 省略前两个维度：批量大小和通道return Y.reshape(Y.shape[2:])# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
X = torch.rand(size=(8, 8))  # 8 * 8 二维
print(comp_conv2d(conv2d, X).shape)

在第一个代码的基础上添加了步幅,即横纵跳跃两格扫描，最后输出[（8 - 3 + 2) / 2 + 1] * [(8 - 3 + 2) / 2 + 1]即4 * 4输出

代码：

import torch
from torch import nn# 为了方便起见，我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):# 这里的（1，1）表示批量大小和通道数都是1X = X.reshape((1, 1) + X.shape)  # 填充两个维度Y = conv2d(X)# 省略前两个维度：批量大小和通道return Y.reshape(Y.shape[2:])# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
X = torch.rand(size=(8, 8))  # 8 * 8 二维
print(comp_conv2d(conv2d, X).shape)

横向跳三，纵向跳四，输出是[(8 - 3 + 0) / 3 + 1] * [(8 - 5 + 2) / 4 + 1]即2 * 2输出

疑惑拓展：

整个卷积模型一般有很多卷积核，这些卷积核是如何每层每层的更新的？

首先再回忆一下损失函数的求解过程：

深度学习_5_模型拟合_梯度下降原理

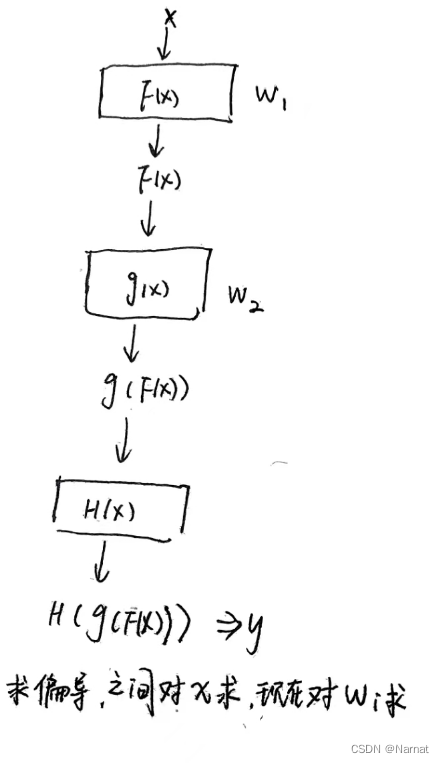
可以看出损失函数中的变量，包含所有卷积核的权重，即所有卷积核的权重都是变量Wi,损失函数正式由这些变量构成，在最后一层卷积核，损失函数由最后一层卷积核输出的值与真实值比较得出。而每一层的梯度即对损失函数求每一层卷积核权重的偏导，这个求偏导的过程一般是反向传递的方式再由求得的梯度去更新每一层的权重

例子：

假设我们有一个两层卷积神经网络，第一层的权重是 W1 ，第二层的权重是 W2 。输入数据是 x，正确的输出是 y来描述反向传递这个过程。