🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 不同情形下检验方式
- 1.1 单正态总体参数的检验
- 1.2 两正态总体参数的检验
- 1.3 成对数据的t检验
- 1.4 单样本比率的检验、两样本比率的检验
- 2 题目实战
- 2.1 题目一:z/u检验
- 2.2 题目二:z/u(t)检验
- 2.3 题目三:t检验
- 2.4 题目四:t检验
- 2.5 题目五:t检验
- 2.6 题目六:t检验
- 2.7 题目七:t检验
- 2.8 题目八:t检验
- 2.9 题目九:F检验
- 2.10 题目十:F检验
- 2.11 题目十一:F(t)检验
- 2.12 题目十二:z/u检验
- 2.13 题目十三:两样本比率检验
- 2.14 题目十四:大样本检验
- 2.15 题目十五:单样本比率检验
- 2.16 题目十六:卡方检验
- 2.17 题目十七:似然检验
- 2.18 题目十八:Fisher精确检验
该篇文章首先介绍了样本不同情形下的检验方式:单正态总体参数的z/t/卡方检验;两正态总体参数的t/F检验;成对数据的t检验;单样本比率检验、两样本比率检验,然后以例题的形式使用R语言编程结合题目背景完成不同情形下的假设检验并给出详细分析。
1 不同情形下检验方式
1.1 单正态总体参数的检验
(1)方差 σ 2 \sigma^2 σ2已知时, μ \mu μ的检验:Z检验。
z.test()
(2)方差 σ 2 \sigma^2 σ2未知时, μ \mu μ的检验:t检验。
t.test()
(3)方差 σ 2 \sigma^2 σ2的检验: χ 2 \chi ^2 χ2检验。
chisq.var.test( )
1.2 两正态总体参数的检验
(1)均值的比较:t检验。
t.test(x, y, var.equal=TRUE)
(2)方差的比较:F检验。
var.test(x, y)
1.3 成对数据的t检验
t.test(x, y, paired=TRUE)
1.4 单样本比率的检验、两样本比率的检验
prop.test( )函数调用格式:prop.test(x, n, p = NULL,alternative = c("two.sided", "less", "greater"),conf.level = 0.95, correct = TRUE)
x为样本中具有某种特性的样本数量, n为样本容量, correct选项为是否做连续性校正。
2 题目实战
2.1 题目一:z/u检验
有一枪弹,出厂时,其初速率v~N(950,100)(单位:m/s).经过较长时间储存,取9发进行测试,得样本值(单位:m/s)如下:914 920 910 934 953 945 912 924 940。据经验,枪弹经储存后其初速率仍服从正态分布,且标准差保持不变,问是否可以认为这批枪弹的初速率有显著降低。 α = 0.05 \alpha=0.05 α=0.05。
运行程序:
z.test<-function(x,n,sigma,alpha,u0=0,alternative="two.sided"){ options(digits=6) #结果显示6为有效数result<-list() #构造一个空的list,用于存放输出结果mean<-mean(x) #求x的算术平均值z<-(mean-u0)/(sigma/sqrt(n)) #计算z统计量的值p<-pnorm(z,lower.tail=FALSE) #返回值是正态分布的分布函数值 result$mean<-mean #将均值存入结果result$z<-z #将z值存入结果 result$p.value<-p #得出P值根据其判定参数估计效果ifelse(alternative=="two.sided",result$p.value <- 2*(1-pnorm(abs(z))), #双侧检验ifelse(alternative=="less",result$p.value <- pnorm(z,lower.tail=T), #下侧检验ifelse(alternative=="greater",result$p.value <-pnorm(z,lower.tail=F),#上侧检验return("your input is wrong"))))result$conf.int<-c(mean-sigma*qnorm(1-alpha/2,mean=0,sd=1,lower.tail=TRUE)/sqrt(n),mean+sigma*qnorm(1-alpha/2,mean=0,sd=1,lower.tail=TRUE)/sqrt(n))result
}
#调用z.test()函数
z.test(928,9,10,0.05,u0=950,alternative="less") #函数中对应的值分别为样本均值、样本数量、总体标准差、置信水平、检验初速率
运行结果:
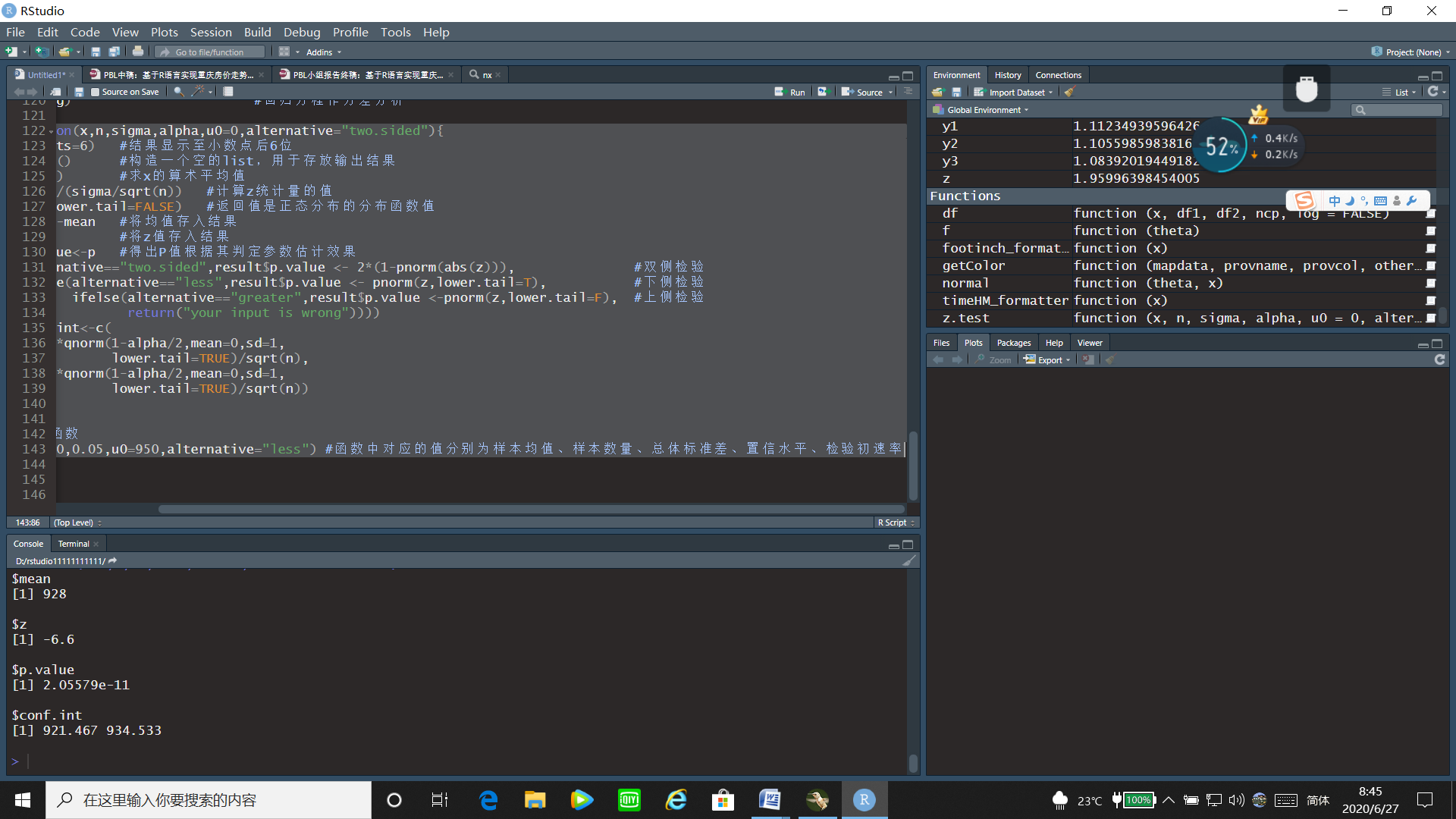
通过u检验的运行结果可以看出z统计量的值为-6.6,置信区间为[921.476, 934.533],p值= 2.05579 e − 11 < 0.05 2.05579e^{-11}<0.05 2.05579e−11<0.05,故拒绝原假设,即可以认为这批枪弹的初速率有显著降低。
2.2 题目二:z/u(t)检验
从一批钢管抽取10根,测得期内径(单位:mm)为:
100.36 100.31 99.99 100.11 100.64
100.85 99.42 99.91 99.35 100.10
设这批钢管内径服从正态分布N(μ,σ2),试分别在下列条件下检验假设。设(α=0.05)。H0:μ=100 vs H1:μ>100。
(1)已知σ=0.5;(z/u检验)
运行程序:
z.test(100.104,10,0.5,0.05,u0=100,alternative="less")#将样本均值、样本数量、总体标准差、置信水平、u0带入计算出均值、检验统计量的值、p值、置信区间。
运行结果:
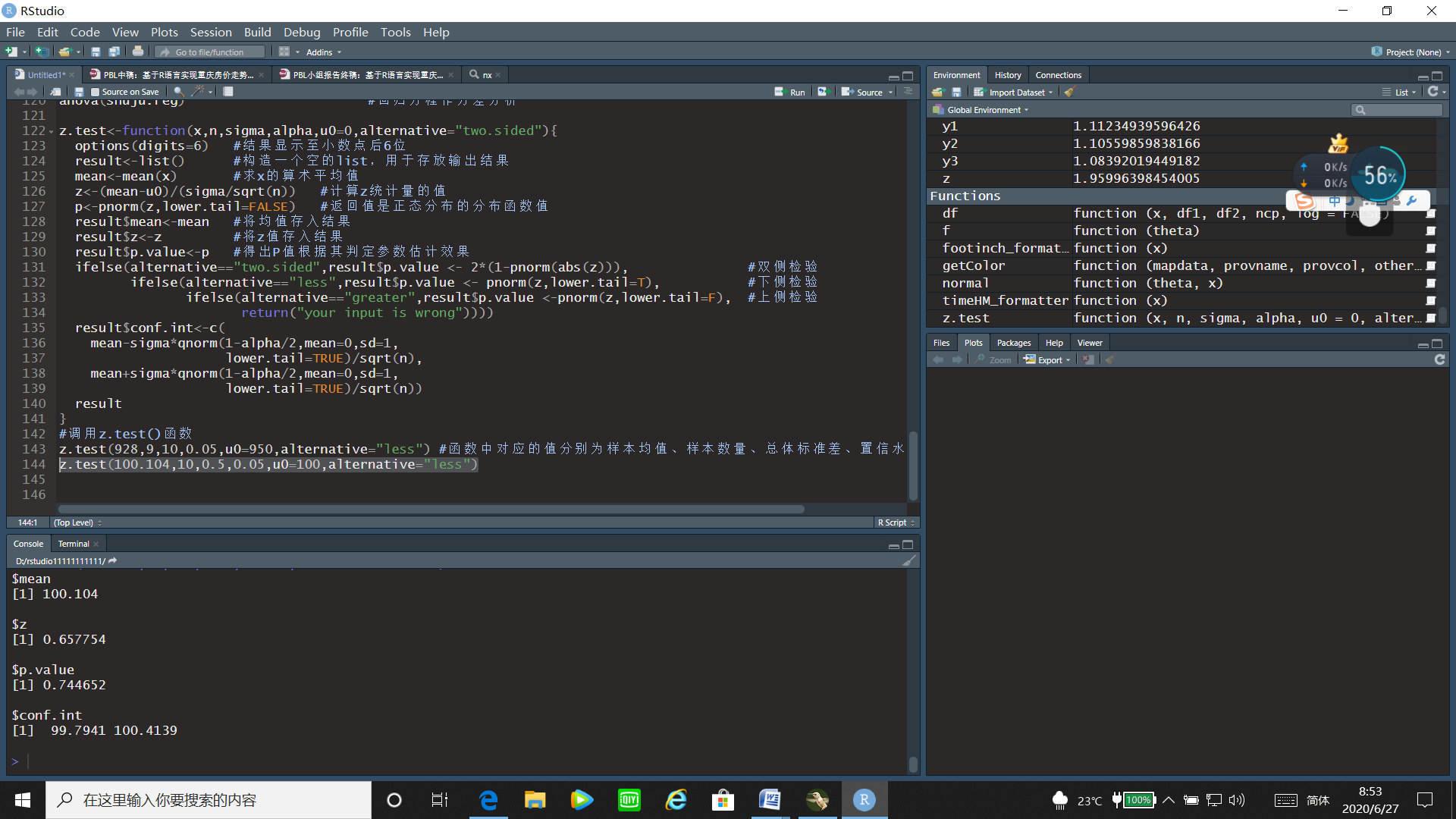
通过u检验的运行结果可以看出z统计量的值为0.657754,置信区间为[99.7941,100.4139],p值=0.744652>0.05,故接受原假设,即不能认为这批钢管内径大于100。
(2)σ未知。(t检验)
运行程序:
salt<-c(100.36,100.31,99.99,100.11,100.64,100.85,99.42,99.91,99.35,100.1)#将样本各个数据定义为一个向量,便于调用
t.test(salt,mu=100,alternative="greater")#将u0等于100带入调用的t检验函数
运行结果:

通过t检验的运行结果可以看出t统计量的值为0.691,p值=0.254>0.05,故接受原假设,即不能认为这批钢管内径大于100。
2.3 题目三:t检验
考察一鱼塘中鱼的含汞量,随机的取10条鱼测得各鱼的含汞量(单位:mg)为:
0.8 1.6 0.9 0.8 1.2 0.4 0.7 1.0 1.2 1.1
设鱼的含汞量服从正态分布N(μ,σ2),试检验假设H0:μ<=1.2 vs H1:μ>1.2 (取α=0.1)。
运行程序:
salt <- c(0.8,1.6,0.9,0.8,1.2,0.4,0.7,1,1.2,1.1)#将样本各个数据定义为一个向量,便于调用
t.test(salt,mu=1.2,alternative="greater",conf.level=0.9)#将u0等于1.2带入调用的t检验函数
运行结果:
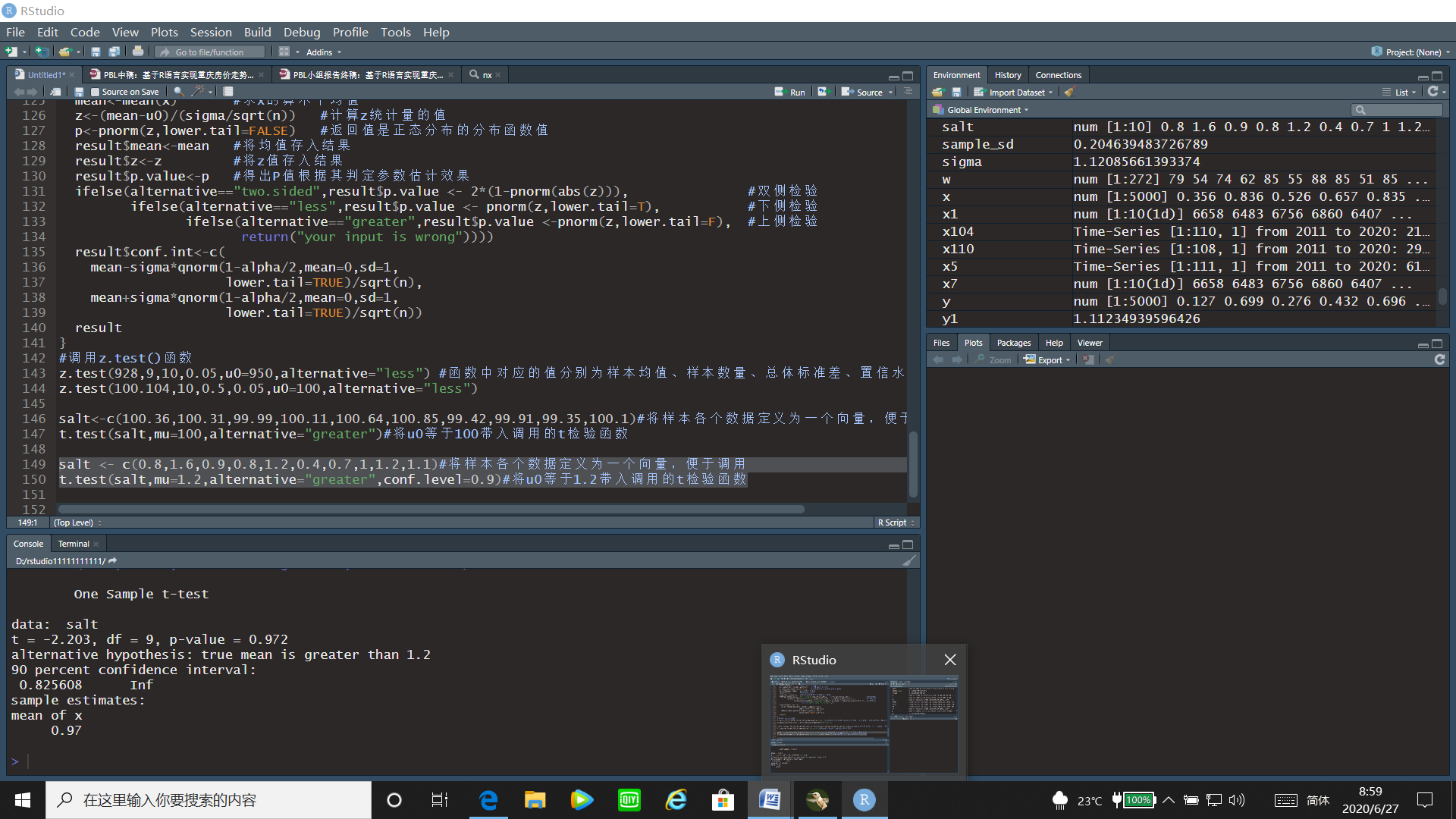
通过t检验的运行结果可以看出t统计量的值为-2.203,p值=0.972>0.05,故接受原假设,即鱼的含汞量没有大于1.2。
2.4 题目四:t检验
如果一个矩形的宽度w与长度l的比w/l=1/2(√5-1)≈0.618,这样的矩形称为黄金矩形。下面列出从某工艺品工厂随机抽取的20个矩形的长度与宽度的比值.
0.693 0.749 0.654 0.670 0.662 0.672 0.615 0.606 0.690 0.628
0.668 0.611 0.606 0.609 0.553 0.570 0.844 0.576 0.933 0.630
设这一工厂生产的矩形长度与宽度的比值总体服从正态分布其均值未μ,试
求检验假设(取α=0.05)。
H0:μ=0.618 vs H1:μ≠0.618。
运行程序:
salt<-c(0.693,0.749,0.654,0.67,0.662,0.672,0.615,0.606,0.69,0.628,0.668,0.611,0.606,0.609,0.553,0.57,0.844,0.576,0.933,0.63)#将样本各个数据定义为一个向量,便于调用
t.test(salt,mu=0.618,alternative="two.sided")#将u0等于0.618带入调用的t检验函数
运行结果:
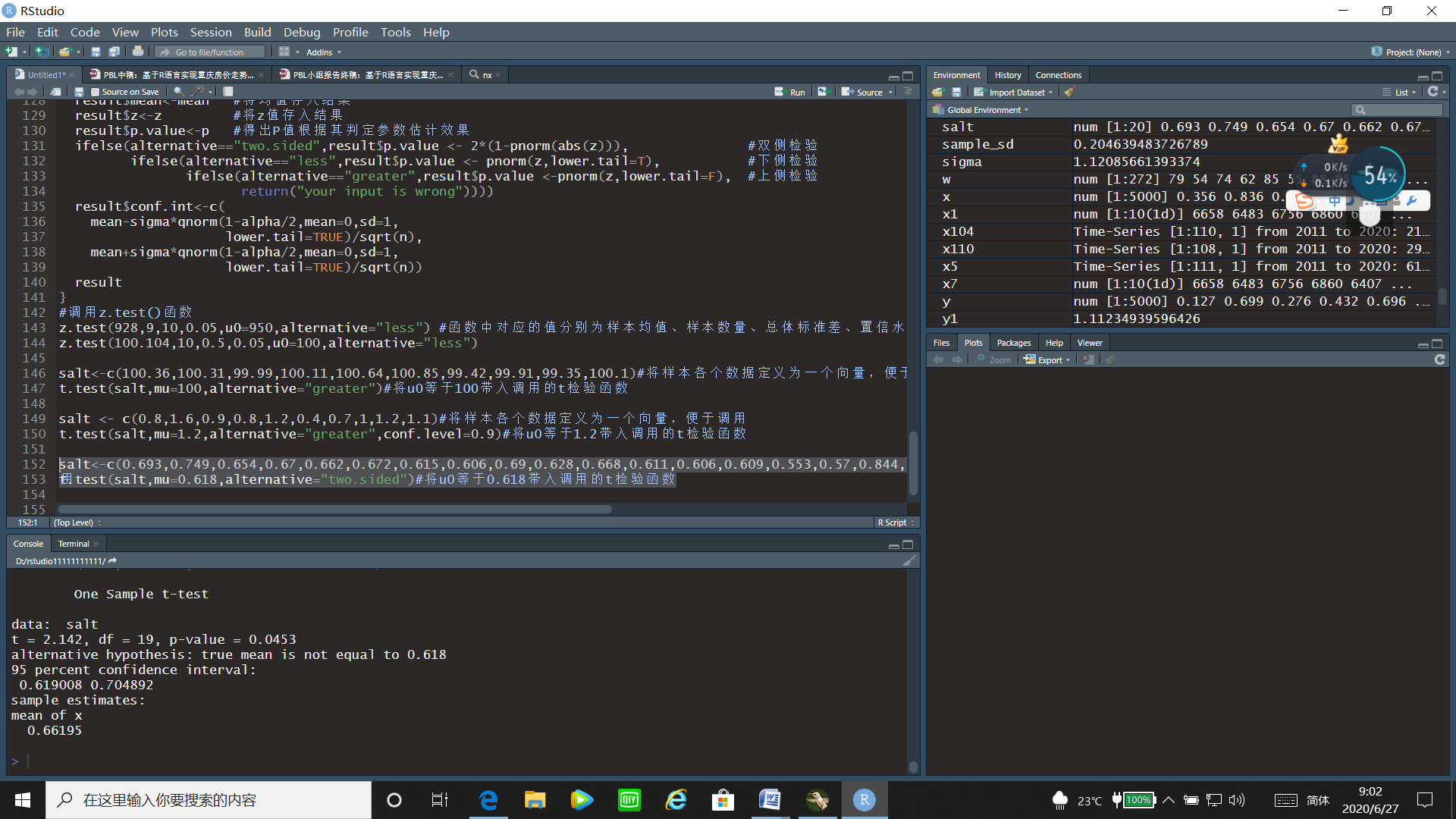
通过t检验的运行结果可以看出t统计量的值为2.142,p值=0.0453<0.05,故拒绝原假设,即不能认为工厂生产的矩形长度与宽度的比值等于0.618。
2.5 题目五:t检验
下面给出两种型号的计算器充电以后所能使用的时间(单位:h)的观测值
型号A:5.5 5.6 6.3 4.6 5.3 5.0 6.2 5.8 5.1 5.2 5.9,
型号B:3.8 4.3 4.2 4.0 4.9 4.5 5.2 4.8 4.5 3.9 3.7 4.6.
设两样本独立且数据所属的两总体的密度函数至多差一个平移量,试问能否
认为型号A的计算器平均使用时间比型号B来的长(取α=0.01)?
运行程序:
x <- c(5.5,5.6,6.3,4.6,5.3,5.0,6.2,5.8,5.1,5.2,5.9)#将型号A的每一个样本值弄成向量
y <- c(3.8,4.3,4.2,4.0,4.9,4.5,5.2,4.8,4.5,3.9,3.7,4.6)#将型号B的每一个样本值弄成向量
t.test(x,y,var.equal=TRUE)#利用t检验函数进行检验
运行结果:
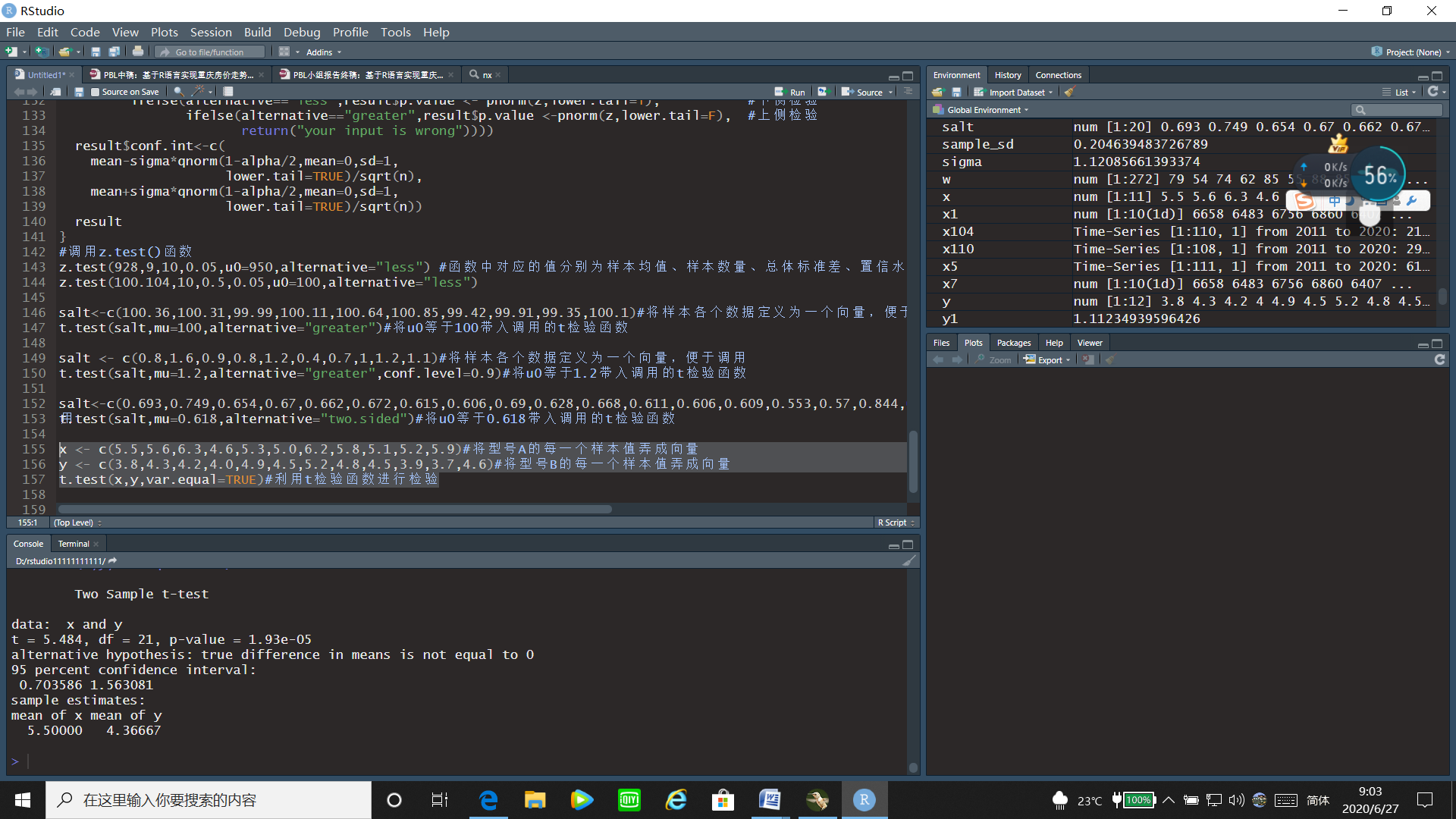
通过t检验的运行结果可以看出t统计量的值为5.484,p值=1.93e-05<0.05,故拒绝原假设,即能认为型号A的计算器平均使用时间比型号B来的长。
2.6 题目六:t检验
在针织品漂白工艺过程中,要考察温度对针织品断裂强力(主要质量标准)的影响.为了比较70oC与80oC的影响有无差别,在这两个温度下,分别重复做了8次试验,得数据如下(单位:N):
70oC时的强力:20.5 18.8 19.8 20.9 21.5 19.5 21.0 21.2
80oC时的强力:17.7 20.3 20.0 18.8 19.0 20.1 20.0 19.1
根据经验,温度对针织品断裂强度的波动没有影响.问在70oC时的平均断裂强力与80oC时的平均断裂强力间是否有显著差别?(假定断裂强力服从正态分布,α=0.05)。
运行程序:
x <- c(20.5,18.8,19.8,20.9,21.5,19.5,21.0,21.2)#将70摄氏度时强力的每一个样本值弄成向量
y <- c(17.7,20.3,20.0,18.8,19.0,20.1,20.0,19.1)#将80摄氏度时强力的每一个样本值弄成向量
t.test(x,y,var.equal=TRUE)
运行结果:
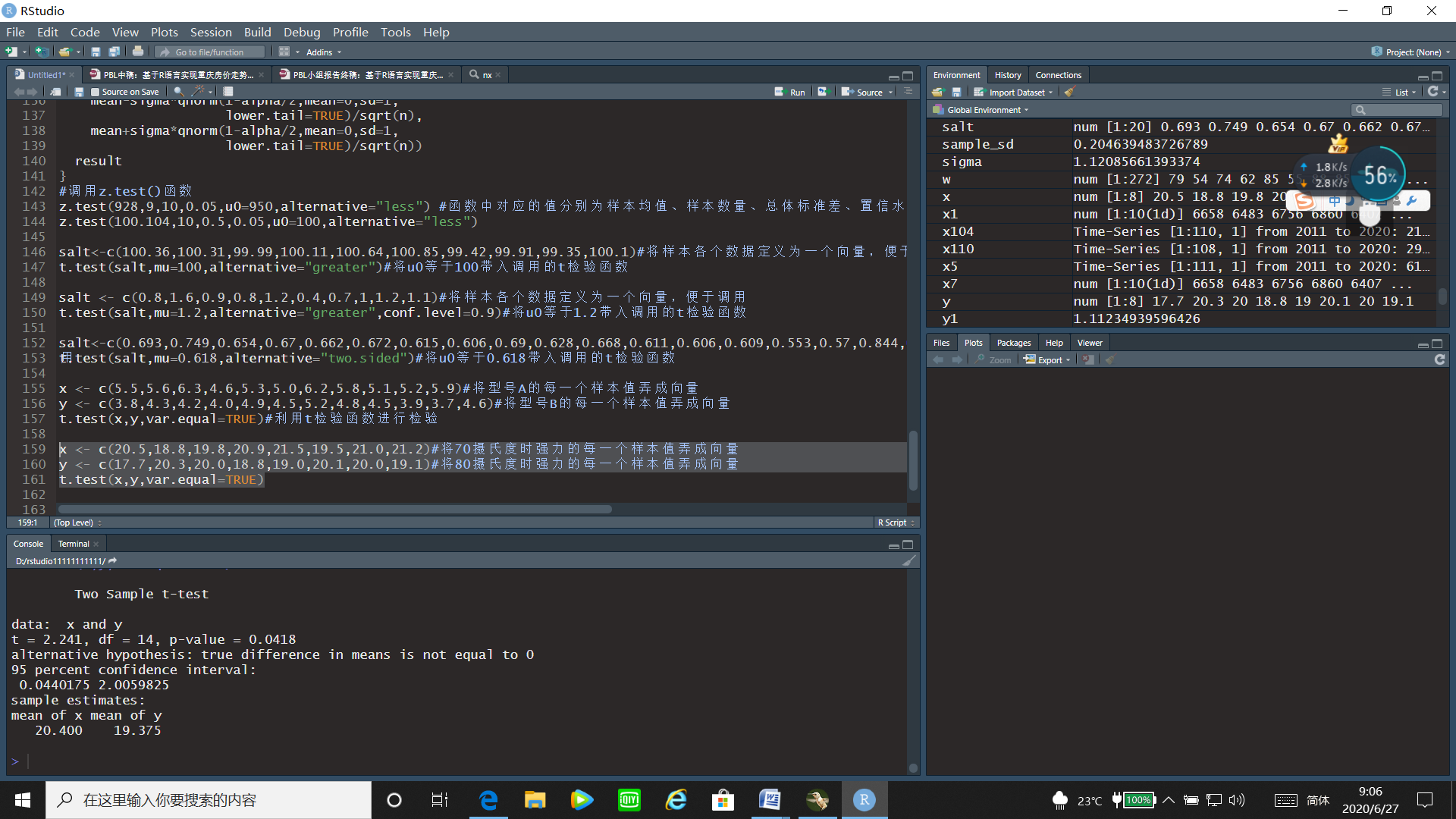
通过t检验的运行结果可以看出t统计量的值为2.241,p值=0.0418<0.05,故拒绝原假设,即在70oC时的平均断裂强力与80oC时的平均断裂强力间有显著差别。
2.7 题目七:t检验
对冷却到-0.72℃的样品用A,B两种测量方法测量其融化到0℃时的潜热,数据如下:
方法A:79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97 80.05 80.03 80.02 80.00 80.02
方法B:80.02 79.94 79.98 79.97 80.03 79.95 79.97 79.97
假设它们服从正态分布,方差相等,试试验:两种测量方法的平均性能是否相等?(取α=0.05)。
运行程序:
x<-c(79.98,80.04,80.02,80.04,80.03,80.03,80.04,79.97,80.05,80.03,80.02,80.00,80.02)#将使用方法A的每一个样本值弄成向量
y <- c(80.02,79.94,79.98,79.97,80.03,79.95,79.97,79.97)#将使用方法B的每一个样本值弄成向量
t.test(x,y,var.equal=TRUE)#利用t检验函数进行检验
运行结果:

通过t检验的运行结果可以看出t统计量的值为3.472,p值=0.00255<0.05,故拒绝原假设,两种测量方法的平均性能不相等。
2.8 题目八:t检验
为了比较测定活水中氯气含量的两种方法,特在各种场合收集到8个污水水样,每个水样均用这两种方法测定氯气含量(单位:mg/l),具体数据如下:
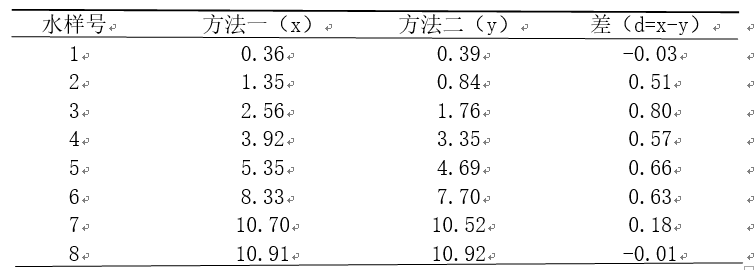
设总体为正态分布,试比较两种测定方法是否有显著差异,请写出检验的p值和结论(取α=0.05)。
运行程序:
x <- c(-0.03, 0.51,0.8,0.57,0.66,0.63,0.18,-0.01)#将差值的到的每一个样本差值弄成向量
t.test(x,mu=0)#利用t检验函数进行检验
运行结果:
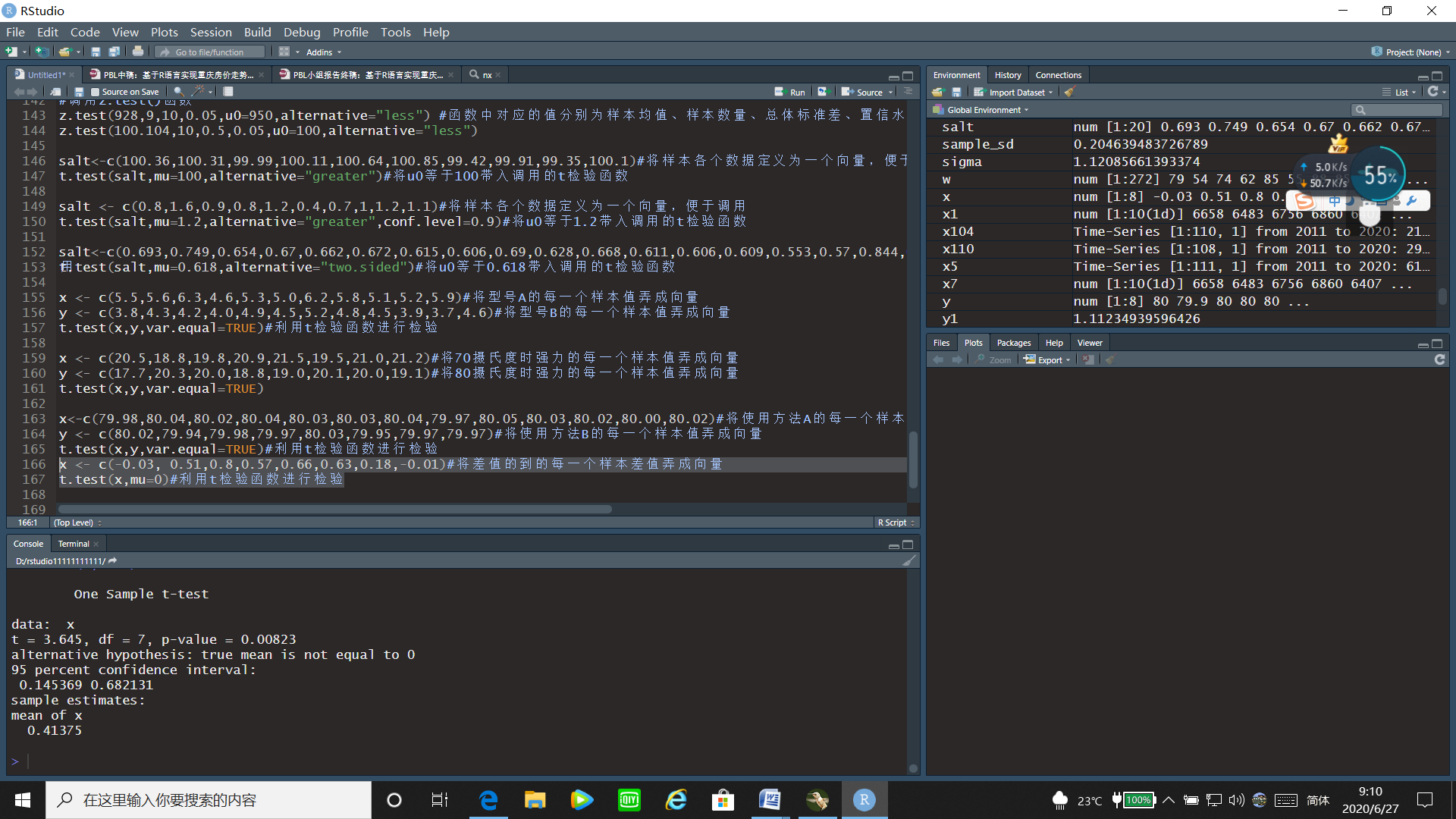
通过t检验的运行结果可以看出t统计量的值为3.645,p值=0.00823<0.05,故拒绝原假设,两种测量方法有显著差异。
2.9 题目九:F检验
为比较不同季节出生的女婴体重的方差,从某年12月和6月出生的女婴中分别随机地抽取6名及10名,测其体重(单位:g)如下:
12月:3520 2960 2560 3260 3960,
06月:3220 3220 3760 3000 2920 3740 3060 3080 2940 3060.
假定新生女婴体重服从正态分布,问新生女婴体重的方差是否是冬季比夏季的小(取α=0.05)?
运行程序:
x <- c(3520,2960,2560,2960,3260,3960)#将12月份每个女婴的体重弄成向量
y <- c(3220,3220,3760,3000,2920,3740,3060,3080,2940,3060)#将6月份每个女婴的体重弄成向量
var.test(x,y)#对假设检验进行F检验
运行结果:
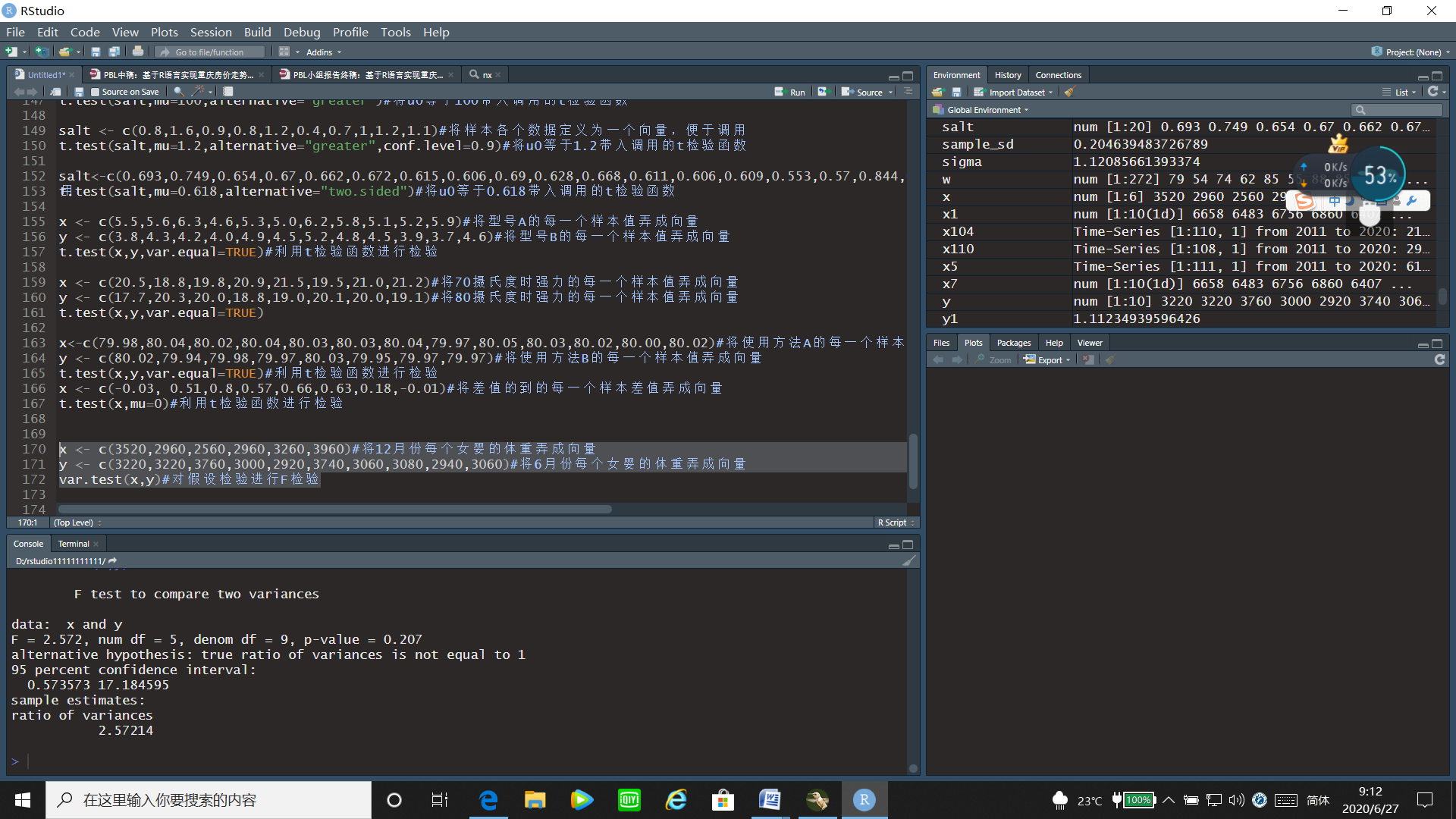
通过F检验的运行结果可以看出F统计量的值为2.572,p值=0.207>0.05,故接受原假设,即认为新生女婴体重的方差冬季不比夏季的小。
2.10 题目十:F检验
两台车床生产同一种滚珠,滚珠直径服从正态分布。从中分别抽取8个和9个产品,测得其直径为
甲车床:15.0 14.5 15.2 15.5 14.8 15.1 15.2 14.8;
乙车床:15.2 15.0 14.8 15.2 15.0 15.0 14.8 15.1 14.8.
比较两台车床生产的滚珠直径的方差是否有明显差异(取α=0.05)。
运行程序:
x <- c(15.0,14.5,15.2,15.5,14.8,15.1,15.2,14.8)#将甲车床生产的滚珠直径样本值弄成向量
y <- c(15.2,15.0,14.8,15.2,15.0,15.0,14.8,15.1,14.8)#将乙车床生产的滚珠直径样本值弄成向量
var.test(x,y)#对假设检验进行F检验
运行结果:
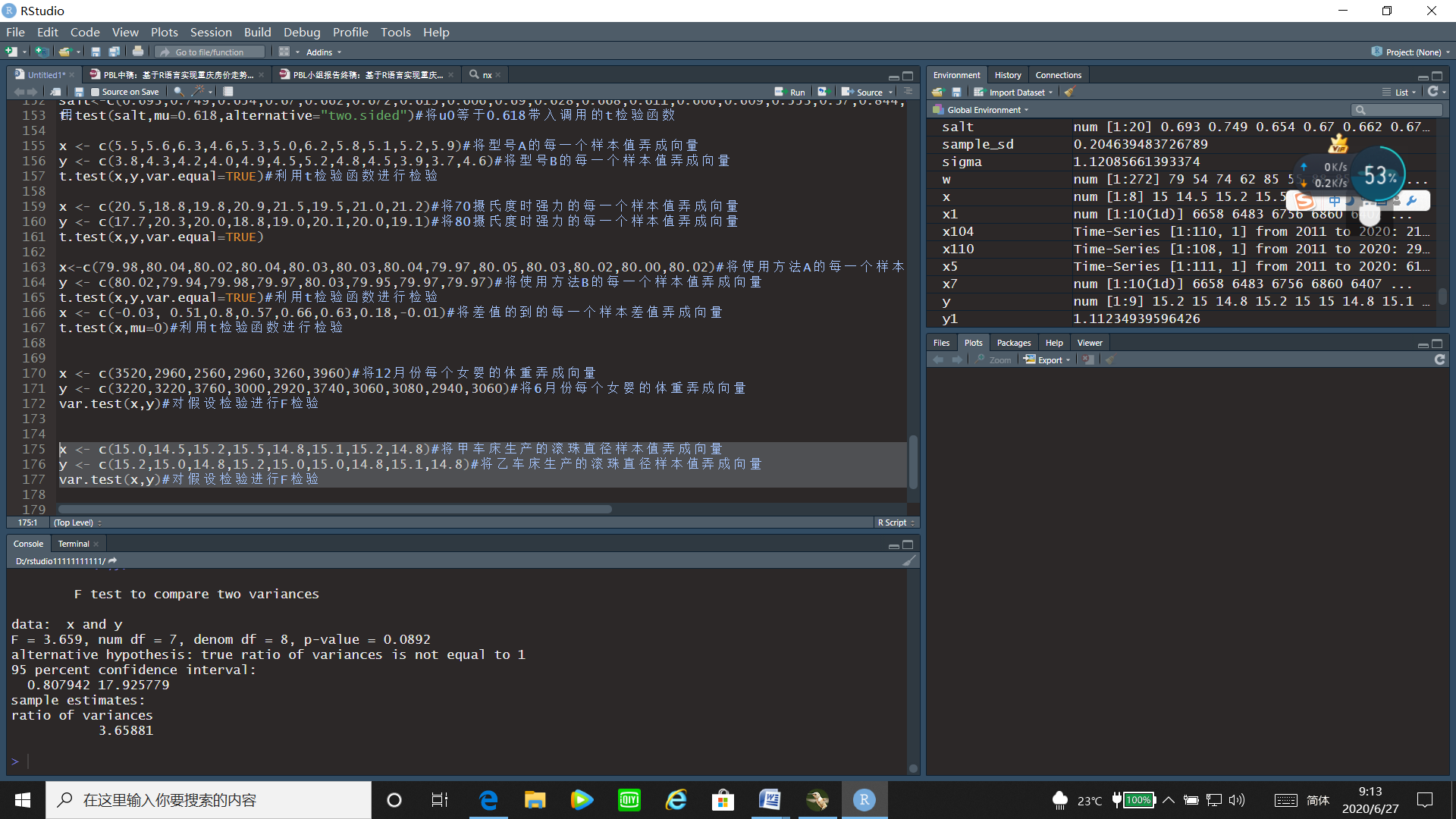
通过F检验的运行结果可以看出F统计量的值为3.659,p值=0.0892>0.05,故接受原假设,即认为两台车床生产的滚珠直径的方差没有明显差异。
2.11 题目十一:F(t)检验
测得两批电子器件的样品的电阻(单位:Ω)为
A批(x):0.140 0.138 0.143 0.142 0.144 0.137;
B批(y):0.135 0.140 0.142 0.136 0.138 0.140.
设这两批器材的电阻值分别服从分布N(μ1,σ1²),N(μ2,σ2²),且两样本独立。
(1)试检验两个总体的方差是否相等(取α=0.05)?:F检验
运行程序:
x <- c(0.140,0.138,0.143,0.142,0.144,0.137)#将A批样本电阻值弄成向量
y <- c(0.135,0.140,0.142,0.136,0.138,0.140)#将B批样本电阻值弄成向量
var.test(x,y)#对假设检验进行F检验
运行结果:

通过F检验的运行结果可以看出F统计量的值为1.108,p值=0.913>0.05,故接受原假设,即可以认为两总体的方差相等。
(2)试检验两个总体的均值是否相等(取α=0.05)?:t检验
运行程序:
x <- c(0.140,0.138,0.143,0.142,0.144,0.137)#将A批样本电阻值弄成向量
y <- c(0.135,0.140,0.142,0.136,0.138,0.140)#将B批样本电阻值弄成向量
t.test(x,y,var.equal=TRUE)#对假设检验进行t检验
运行结果:
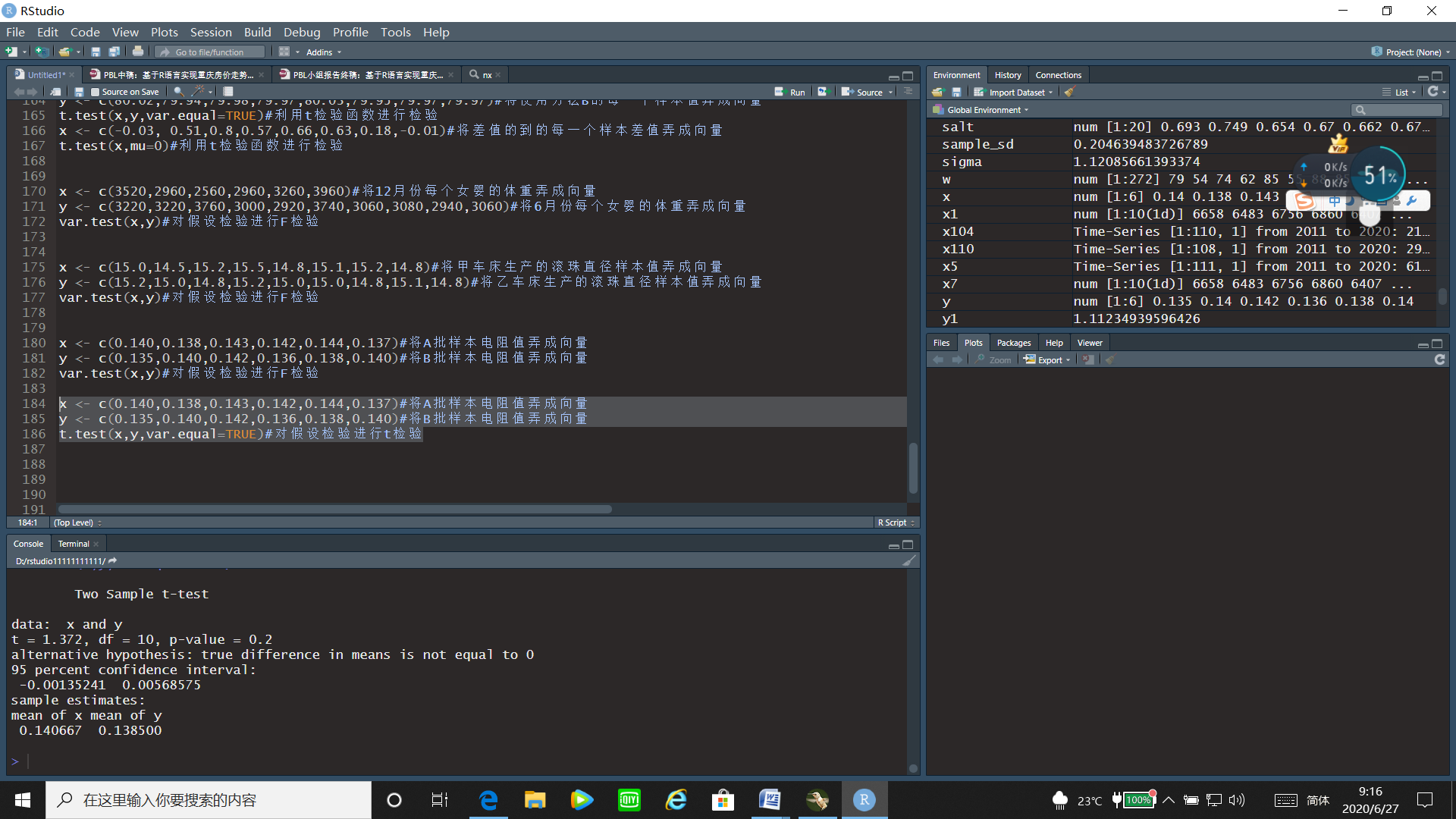
通过t检验的运行结果可以看出t统计量的值为1.372,p值=0.2>0.05,故接受原假设,即可以认为两总体的均值相等。
2.12 题目十二:z/u检验
从一批服从指数分布的产品中抽取10个进行寿命试验,观测值如下(单位:h):
1643 1629 426 132 1522 432 1759 1074 528 283.
根据这批数据能否认为其平均寿命不低于1100h(取α=0.05)?
运行程序:
z.test=function(x,mu,sigma,theta,alternative="two.sided"){n=length(x)result=list() #构造一个空的list,用于存放输出结果mean=mean(x)z=2*n*mean/theta#计算z统计量的值options(digits=4)#结果显示至小数点后4位result$mean=mean;result$z=z #将均值、z值存入结果result$P=2*pnorm(abs(z),lower.tail=FALSE) #根据z计算Pif(alternative=="greater") result$P=pnorm(z,lower.tail=FALSE)else if(alternative=="less") result$P=pnorm(z)result}
data=c(1643,1629,426,132,1522,432,1759,1074,528,283)
z.test(x=data,theta=1100,alternative="less")
运行结果:
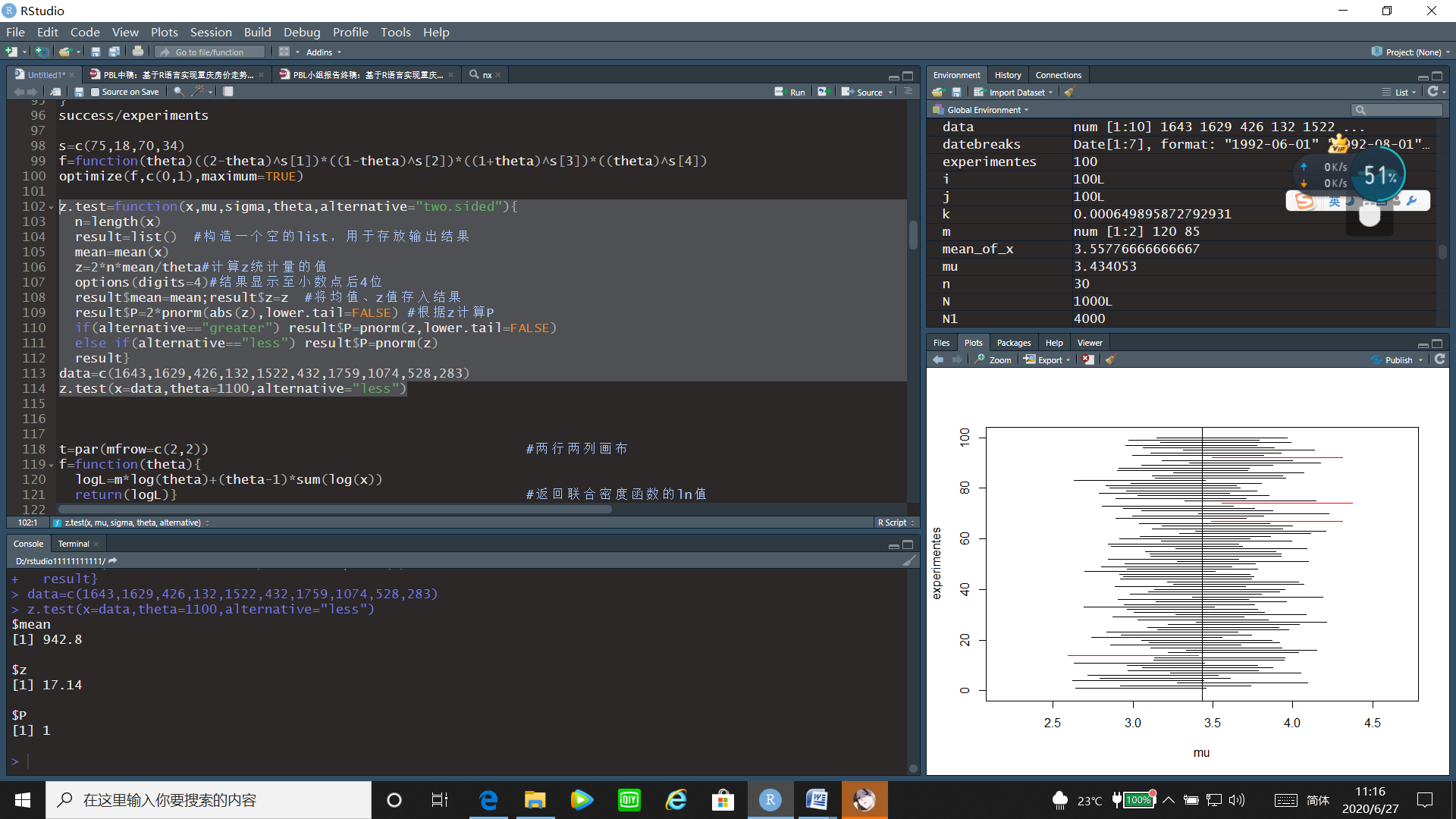
接受原假设,可以认为其平均寿命不低于1100h。
2.13 题目十三:两样本比率检验
某大学随机调查120名男同学,发现有50人非常喜欢看武侠小说,而随机查的85名女同学中有23人喜欢,用大样本检验方法在α=0.05下确认:男女同学在喜爱武侠小说方面有无显著差异?并给出检验的p值。
运行程序:
n <-c (50,23) #样本中喜欢看武侠小说的人数
m <-c (120,85) #两样本的样本容量
prop.test(n,m) #选取大样本检验
运行结果:
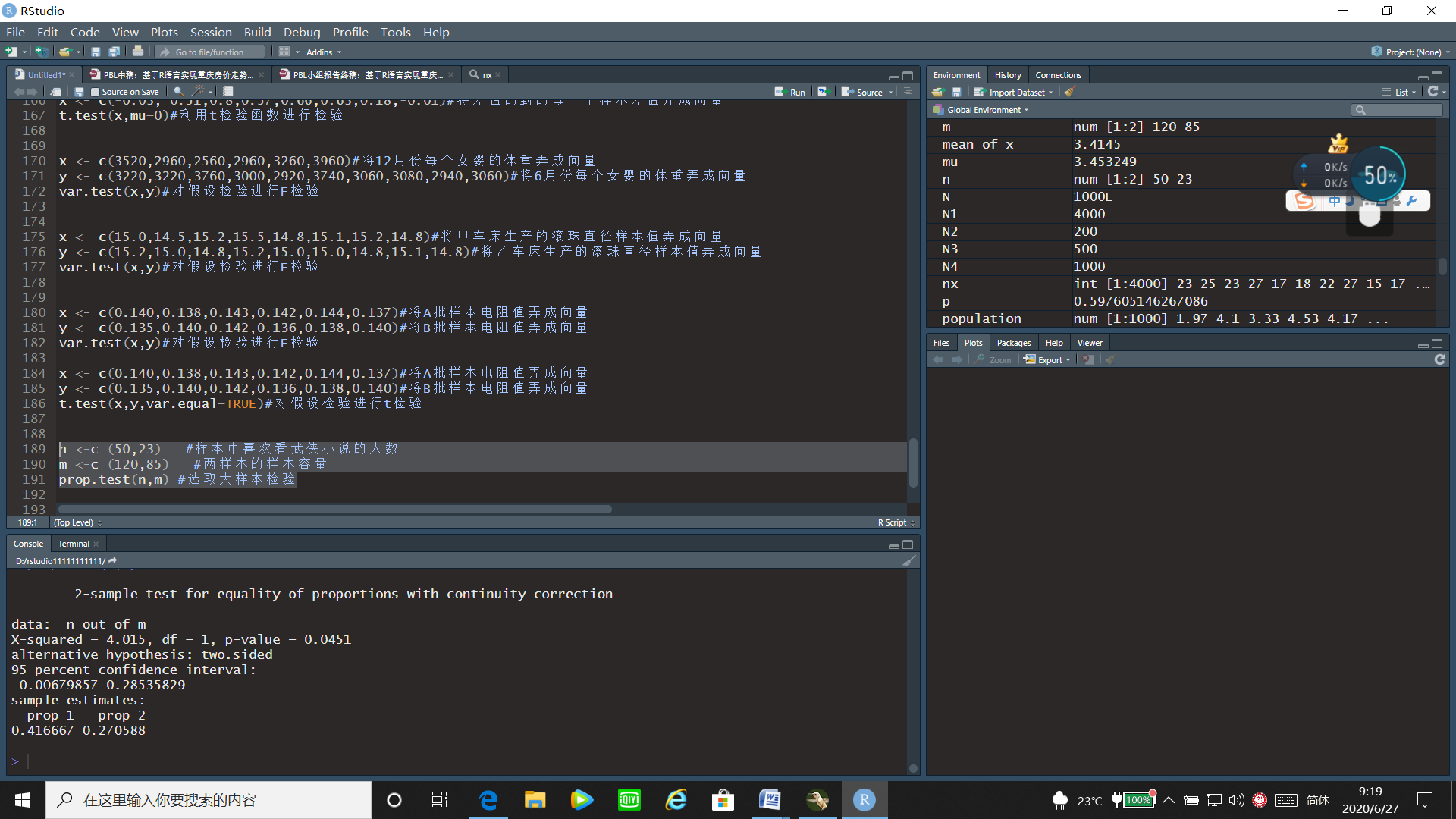
通过大样本检验的运行结果可以看出X统计量为4.015,p值=0.0451<0.05,故拒绝原假设,即认为男女同学在喜爱武侠小说方面有显著差异。
2.14 题目十四:大样本检验
若在猜硬币正反面游戏中,某人在100次试猜中共猜中60次,你认为他是否有诀窍?(取α=0.05)。
运行程序:
binom.test(60,100,p=0.5,alternative="greater")
#使用binom.test()进行大样本检测
运行结果:

通过大样本检验的运行结果可以看出p值=0.0284<0.05,故拒绝原假设,即认为他有诀窍。
2.15 题目十五:单样本比率检验
若在猜硬币正反面游戏中,某人在100次试猜中共猜中60次,你认为他是否有诀窍?(取α=0.05)。
运行程序:
prop.test(60,100,correct=TRUE)
运行结果:
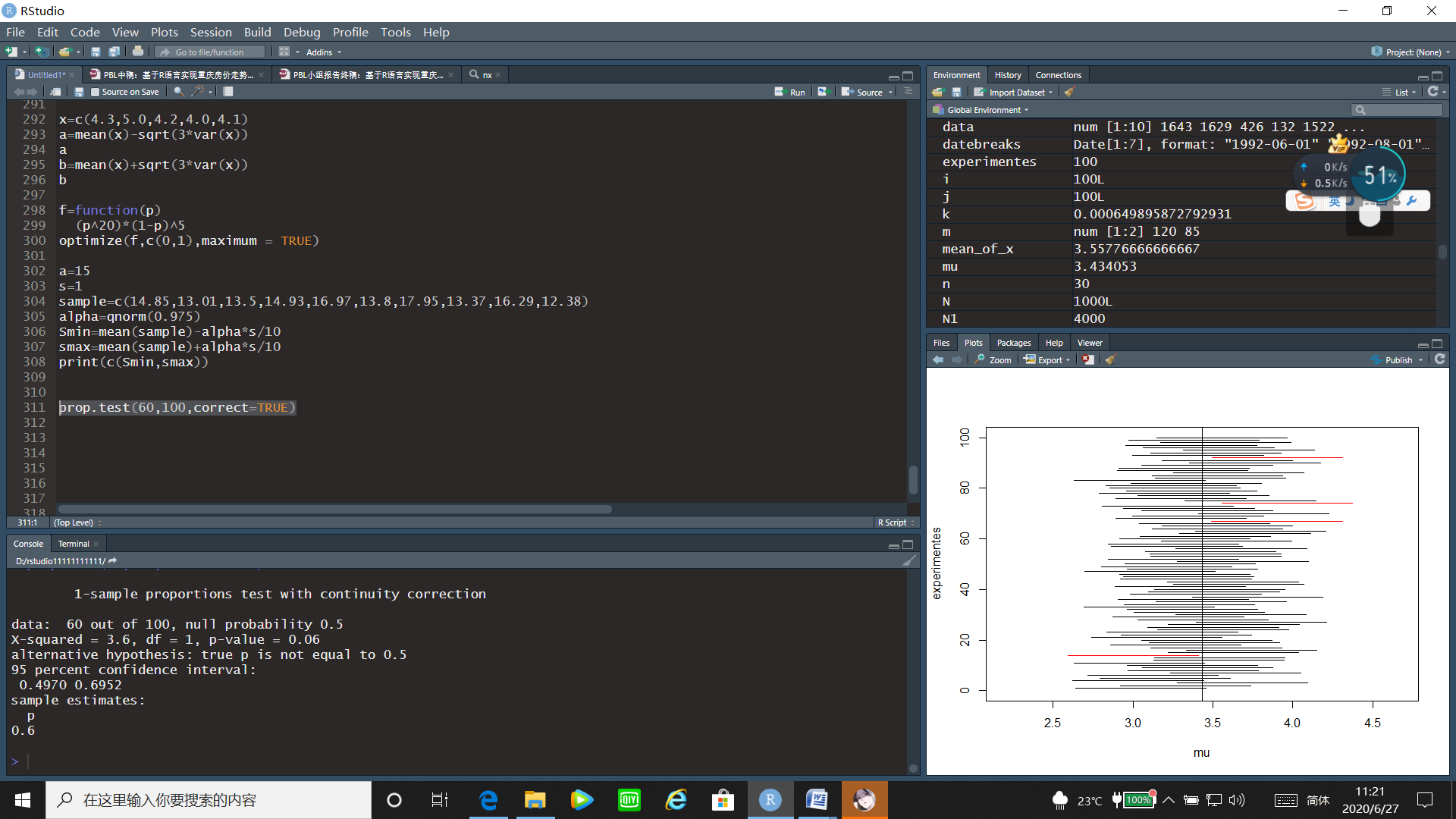
接受原假设,有诀窍。
2.16 题目十六:卡方检验
检查了一本书的100页,记录各页中的印刷错误的个数,其结果如下:

问能否认为一页的印刷错误个数服从泊松分布?(取α=0.05)。
运行程序:
z<-(35+40+19+3+2+1)/100
chisq.fit<-function(x,y,r){options(digits=4) #结果显示至小数点后4位result<-list() #构造一个空的list,用于存放输出结果n<-sum(y)prob<-dpois(x,z,log=FALSE) #z为极大似然估计值y<-c(y,0)m<-length(y) #m的长度为yprob<-c(prob,1-sum(prob))result$chisq<-sum((y-n*prob)^2/(n*prob))result$p.value<-pchisq(result$chisq,m-r-1,lower.tail=FALSE)result
}x<-c(0,1,2,3,4,5)
y<-c(35,40,19,3,2,1)
chisq.fit(x,y,1)
运行结果:
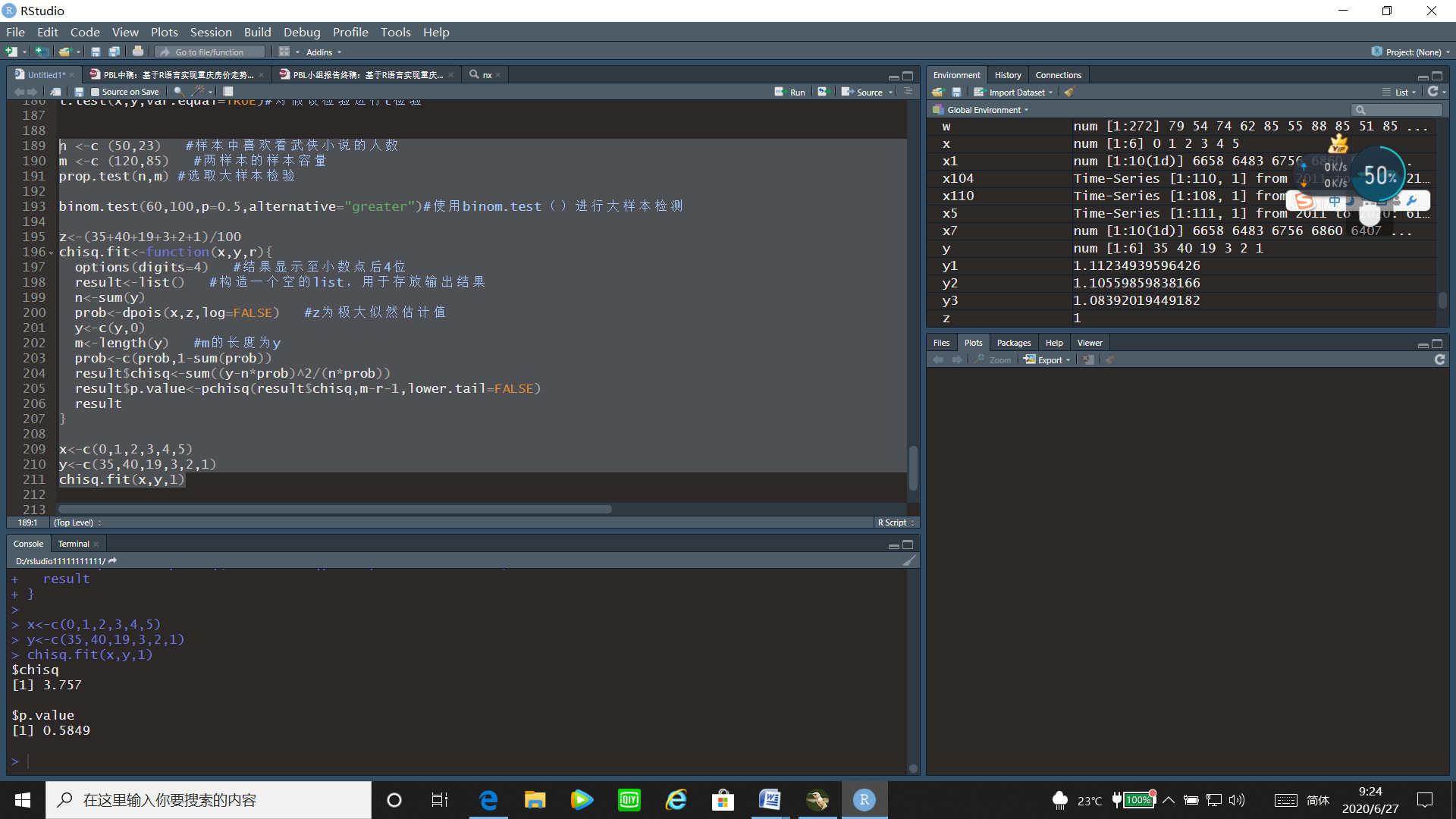
通过运行结果,可以看出p值=0.5849>0.05,故接受原假设,即认为一页的印刷错误个数服从泊松分布。
2.17 题目十七:似然检验
某种配偶的后代按体格的属性分为三类,各类的数目分别是10,53,46.按照某种遗传模型其频率之比应为p²:2p(1-p):(1-p)²,问数据与模型是否相符(α=0.05)?
运行程序:
N<-c(10,53,46)
n<-N[1]+N[2]+N[3]
f<-function(p){ #定义函数f用以表示似然函数p^(2*N[1]+N[2])*(1-p)^(N[2]+2*N[3])
}
mle<-optimize(f,c(0,1),maximum = TRUE) #求极大似然估计
a<-mle$maximum #所求极大似然估计
b<-c(a^2,2*a*(1-a),(1-a)^2) #b分别表示p1,p2,p3的值
c<-(N[1]-n*b[1])^2/(n*b[1])+(N[2]-n*b[2])^2/(n*b[2])+(N[3]-n*b[3])^2/(n*b[3])
p<-1-pchisq(c,1)
a
b
c
p
运行结果:
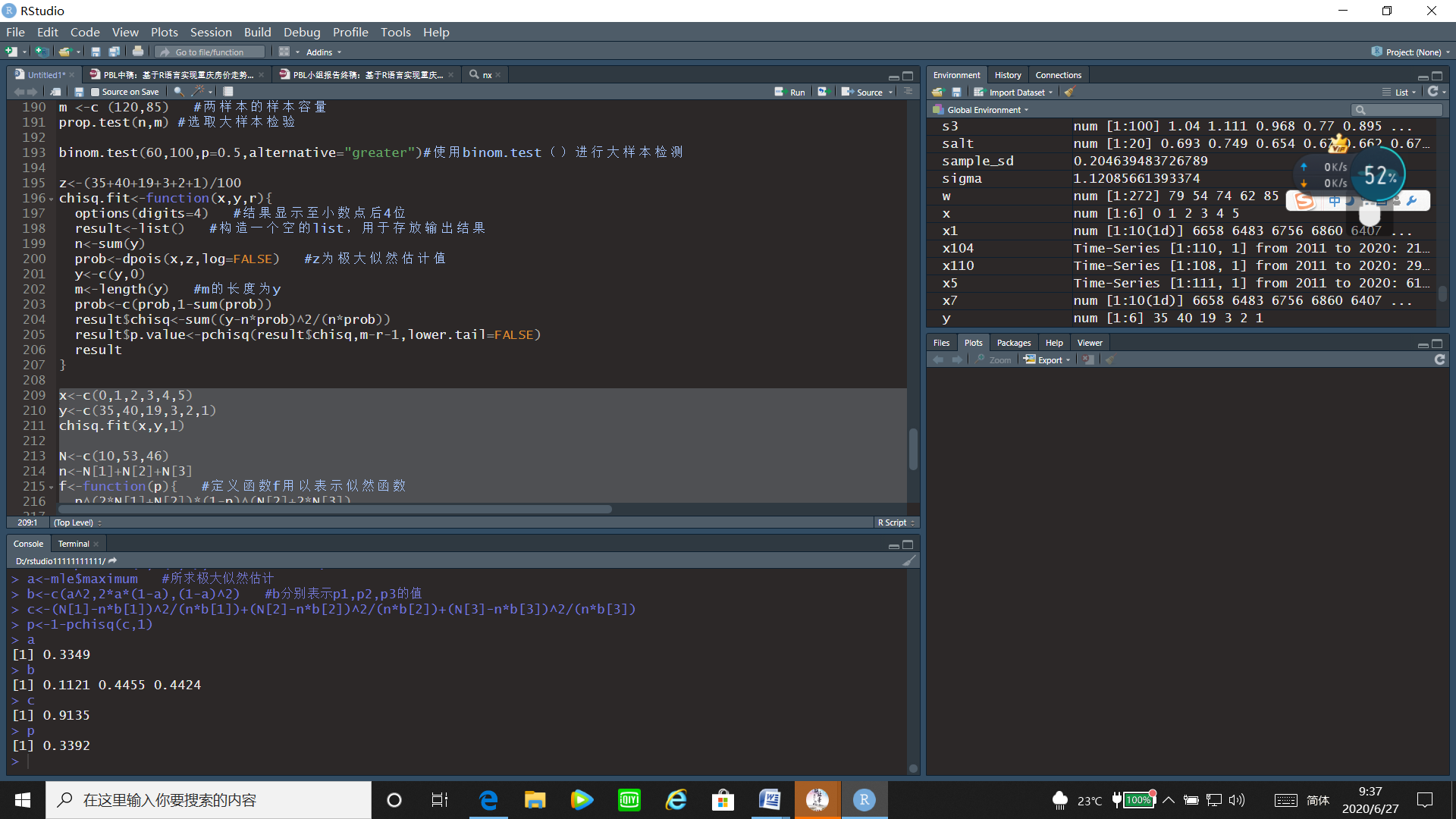
通过运行结果,可以看出p值=0.3392>0.05,故接受原假设,即认为数据与模型相符合。
2.18 题目十八:Fisher精确检验
一项是否应提高小学生的计算机课程的比例的调查结果如下:

问年龄因素是否影响了对问题的回答(α=0.05)?
运行程序:
a<-matrix(c(32,44,47,28,21,12,14,17,13),
nr=3, #分类组数为3dimnames=list(c("55+","36~55","15~35"),c("agree","disagree","don't know")))
fisher.test(a) #Fisher精确检验
运行结果:
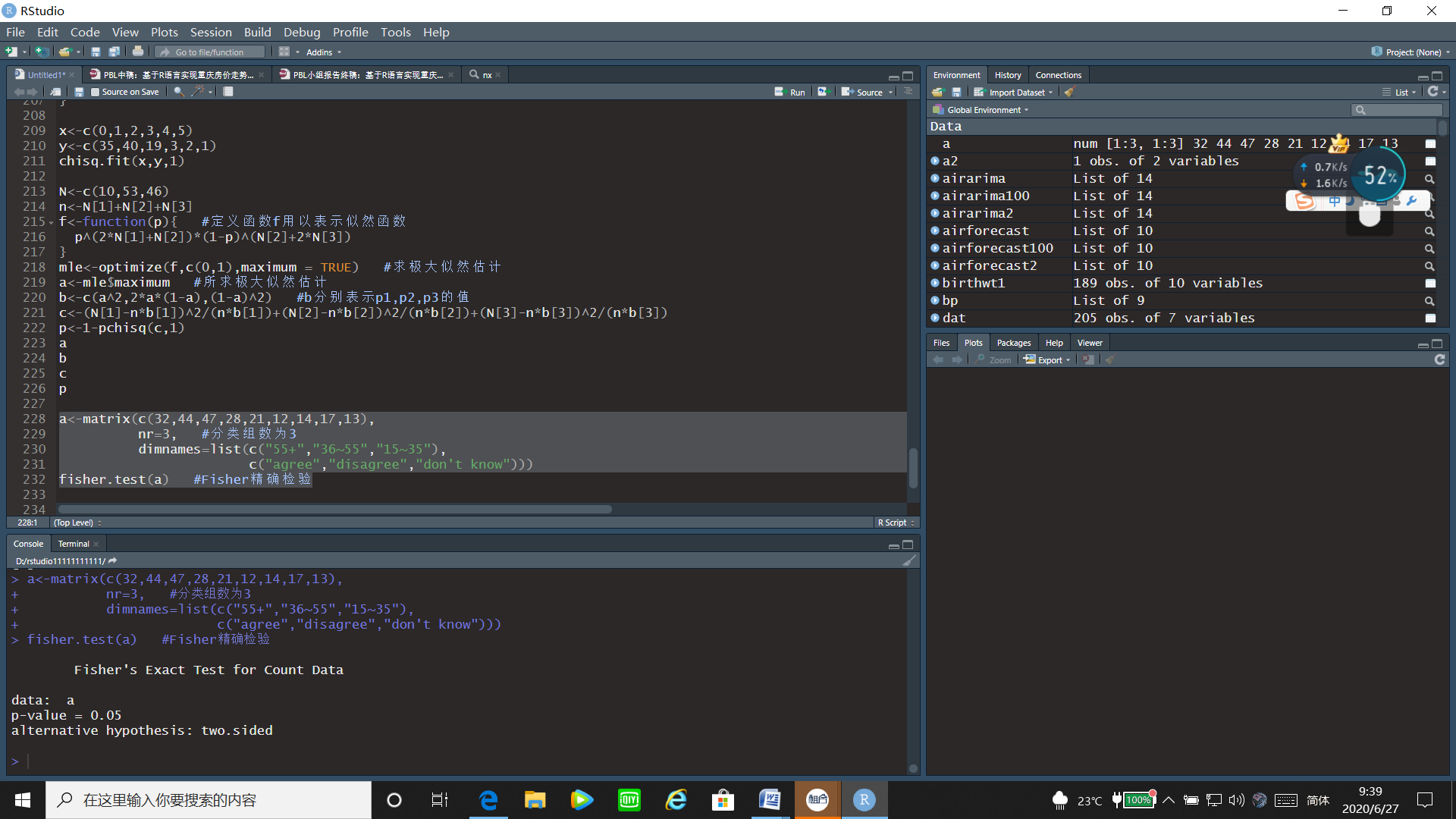
通过运行结果,可以看出p值=0.05≤0.05,故拒绝原假设,即认为年龄因素影响了对问题的回答。






)



![Android Selinux详解[五]--新增hal服务标签相关](http://pic.xiahunao.cn/Android Selinux详解[五]--新增hal服务标签相关)

)



—— 怎么玩(3))
之requests模块)

