一、什么是大顶堆？

大顶堆（Max Heap）是一种二叉堆的实现，它满足以下性质：

1. 任意节点的值都大于等于其子节点的值。
2. 根节点（堆顶）的值是整个堆中最大的。

大顶堆通常用于实现优先队列等数据结构，其中需要快速访问和删除最大元素。它的实现通常是通过数组来完成的，其中父节点和子节点的关系可以用数组的索引来表示。

在大顶堆中，如果一个节点的索引是i，那么它的左子节点的索引是2i+1，右子节点的索引是2i+2。

大顶堆的一些基本操作包括：

1. 插入元素：将新元素插入到堆的末尾，然后通过一系列交换操作将其上移，以维持堆的性质。
2. 删除堆顶元素：将堆顶元素与末尾元素交换，然后移除末尾元素并通过一系列交换操作将新的堆顶元素下移，以维持堆的性质。
3. 构建堆：将一个无序数组转换成一个大顶堆，通常采用从后往前遍历数组进行堆化操作。
4. 堆排序：利用大顶堆进行排序，首先构建大顶堆，然后反复将堆顶元素与末尾元素交换并维护堆的性质，直到整个数组有序。

大顶堆的时间复杂度如下：

• 插入元素：O(log n)
• 删除堆顶元素：O(log n)
• 构建堆：O(n)
• 堆排序：O(n log n)

二、举一个大顶堆的例子

假设我们有一个包含以下整数的数组：[10, 20, 15, 30, 40, 5]

我们将通过构建一个大顶堆来演示。首先，我们从数组的末尾开始构建堆。

1. 为了有效地构建大顶堆，我们需要从最后一个非叶子节点开始向前进行堆化操作。最后一个非叶子节点的索引可以通过数组长度的一半减去1来计算，因为最后一个非叶子节点的索引是最后一个节点的父节点。本例子中最后一个非叶子节点是15。                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

   

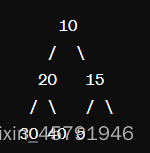
2.调整15之前的节点

• 对于节点20：20 > 30 和 40，不需要调整。

• 对于节点10：10 < 20 和 15，交换10和20的位置，得到：

 

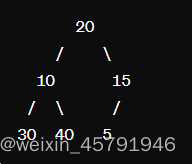
3. 继续堆化节点10。10 < 30 和 40，交换10和30的位置 

4.继续堆化节点20。20 > 10 和 15，不需要调整。

5. 继续堆化节点15。15 < 5，交换15和5的位置。

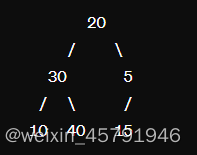
三、如何用Python实现大顶堆

class MaxHeap:def __init__(self):self.heap = []def insert(self, val):self.heap.append(val)self._percolate_up(len(self.heap) - 1)def extract_max(self):if not self.heap:return Noneif len(self.heap) == 1:return self.heap.pop()max_val = self.heap[0]self.heap[0] = self.heap.pop()self._percolate_down(0)return max_valdef _percolate_up(self, idx):parent_idx = (idx - 1) // 2while idx > 0 and self.heap[idx] > self.heap[parent_idx]:self.heap[idx], self.heap[parent_idx] = self.heap[parent_idx], self.heap[idx]idx = parent_idxparent_idx = (idx - 1) // 2def _percolate_down(self, idx):left_child_idx = 2 * idx + 1right_child_idx = 2 * idx + 2max_idx = idxif left_child_idx < len(self.heap) and self.heap[left_child_idx] > self.heap[max_idx]:max_idx = left_child_idxif right_child_idx < len(self.heap) and self.heap[right_child_idx] > self.heap[max_idx]:max_idx = right_child_idxif max_idx != idx:self.heap[idx], self.heap[max_idx] = self.heap[max_idx], self.heap[idx]self._percolate_down(max_idx)# 示例用法
max_heap = MaxHeap()
max_heap.insert(10)
max_heap.insert(20)
max_heap.insert(15)
max_heap.insert(30)
max_heap.insert(40)
max_heap.insert(5)print(max_heap.heap)  # 输出: [40, 30, 15, 10, 20, 5]print(max_heap.extract_max())  # 输出: 40
print(max_heap.heap)  # 输出: [30, 20, 15, 10, 5]