如果给定一个含有环的有向图，要在这个图中找出所有的环并计算这些环的路径长度，然后除以环的边数，所得到的结果也就是环的平均值，这里也就是如何计算这个环的最小均值问题。

首先可以确定的是，如果图中均值最小的环的值是0，那么图中就不包含负环，由于是负环，那么所有边加总就是负数，显然将所有边加总后除以边的数量依然是负数，这就与均值最小的环值为0所相矛盾，给定一个图，要寻找最短均值回路，如下图所示：

添加图片注释，不超过 140 字（可选）

从图中可以计算出由虚线构成的环的均值是最小的，

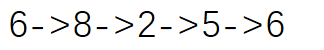
添加图片注释，不超过 140 字（可选）

其均值是：

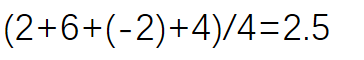
添加图片注释，不超过 140 字（可选）

而使用python实现的代码如下：

import numpy as np
vertex_list = [0, 1, 2, 3, 4, 5, 6, 7, 8] #记录图中所有节点 
edge_vertex = {} #记录相连节点
edge_vertex[0] = [7]
edge_vertex[1] = [0, 2]
edge_vertex[2] = [3,8]
edge_vertex[3] = [5]
edge_vertex[4] = [3]
edge_vertex[5] = [4, 2]
edge_vertex[6] = [5, 7]
edge_vertex[7] = [1]
edge_vertex[8] = [6, 7]
edges = np.zeros((len(vertex_list), len(vertex_list))).astype(int) #记录边的长度
for i in range(len(vertex_list)):for j in range(len(vertex_list)):edges[i][j] = sys.maxsize
edges[0][1] = 4  
edges[1][7] = 11
edges[7][0] = 8
edges[2][1] = 8
edges[2][5] = 4
edges[3][2] = 7
edges[3][4] = 9
edges[4][5] = 10
edges[5][3] = 14
edges[5][6] = 2
edges[6][8] = 6
edges[8][2] = 2
edges[7][6] = 1
edges[7][8] = 7
path_table = np.zeros((len(vertex_list) + 1, len(vertex_list))).astype(int) #第i行第j列表示从起始点0经过i条边后到达节点j的最短路径长度
for i in range(len(vertex_list) + 1):for j in range(len(vertex_list)):path_table[i][j] = sys.maxsize
path_table[0][0] = 0 #起始点通过0条边抵达自己
#%%
def  compute_path_table(k, v):if k < 0 or k > len(vertex_list):return sys.maxsizeif v < 0 or v >= len(vertex_list):return sys.maxsizeif k == 0:return path_table[k][v]if path_table[k][v] != sys.maxsize:return path_table[k][v]for u in edge_vertex[v]:  #根据公式(9)进行计算s_to_u = compute_path_table(k - 1, u)if s_to_u != sys.maxsize  and s_to_u + edges[u][v] < path_table[k][v]:print("u: {0}, k: {1}, s_to_u: {2}, s_to_v: {3}".format(u, k, s_to_u, s_to_u + edges[u][v]))path_table[k][v] = s_to_u + edges[u][v]return path_table[k][v]
for k in range(len(vertex_list) + 1):for v in vertex_list:compute_path_table(k, v)