目录
1.算法流程简介
2.1.K-mean算法核心代码
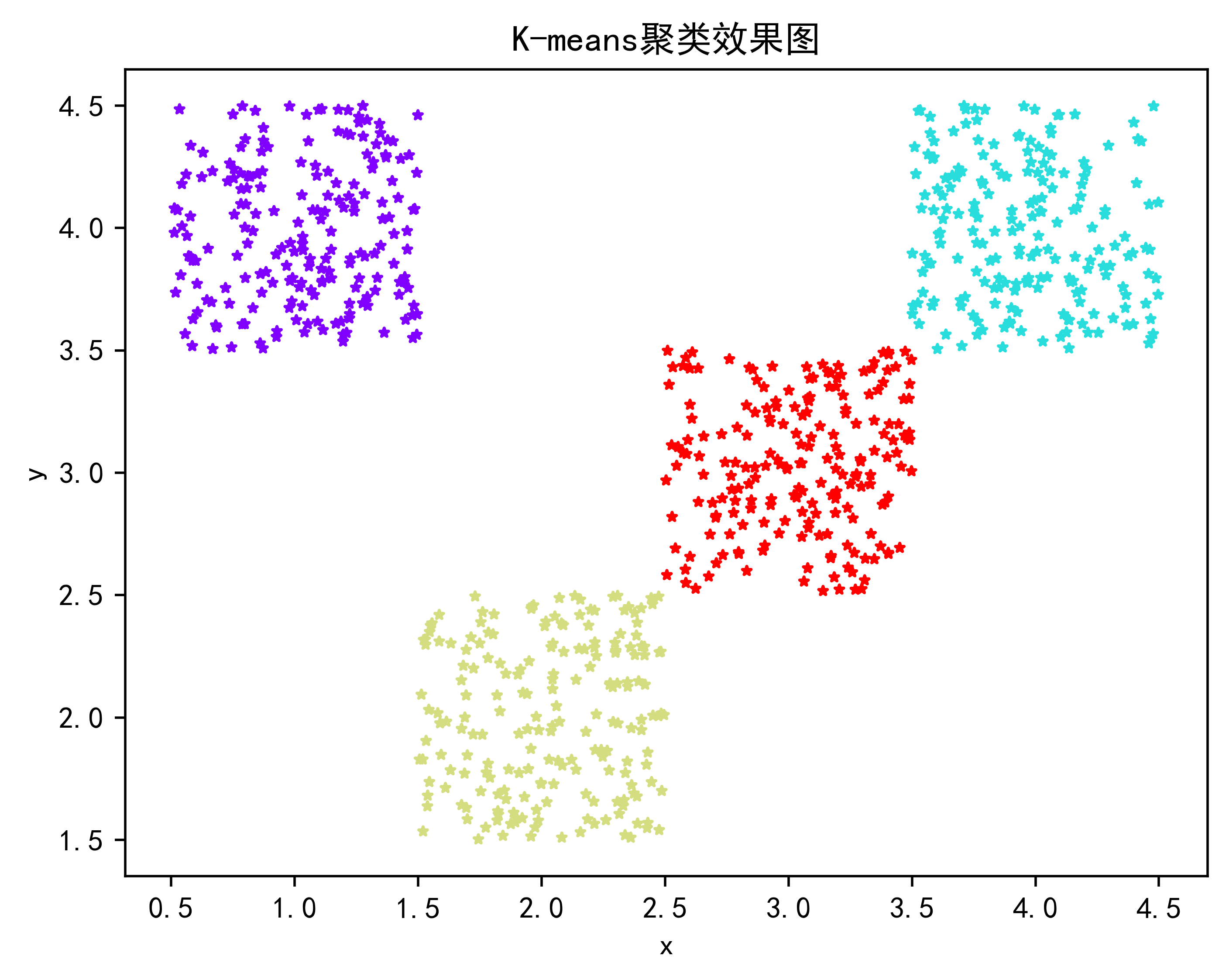
2.2.K-mean算法效果展示
3.1.肘部法算法核心代码
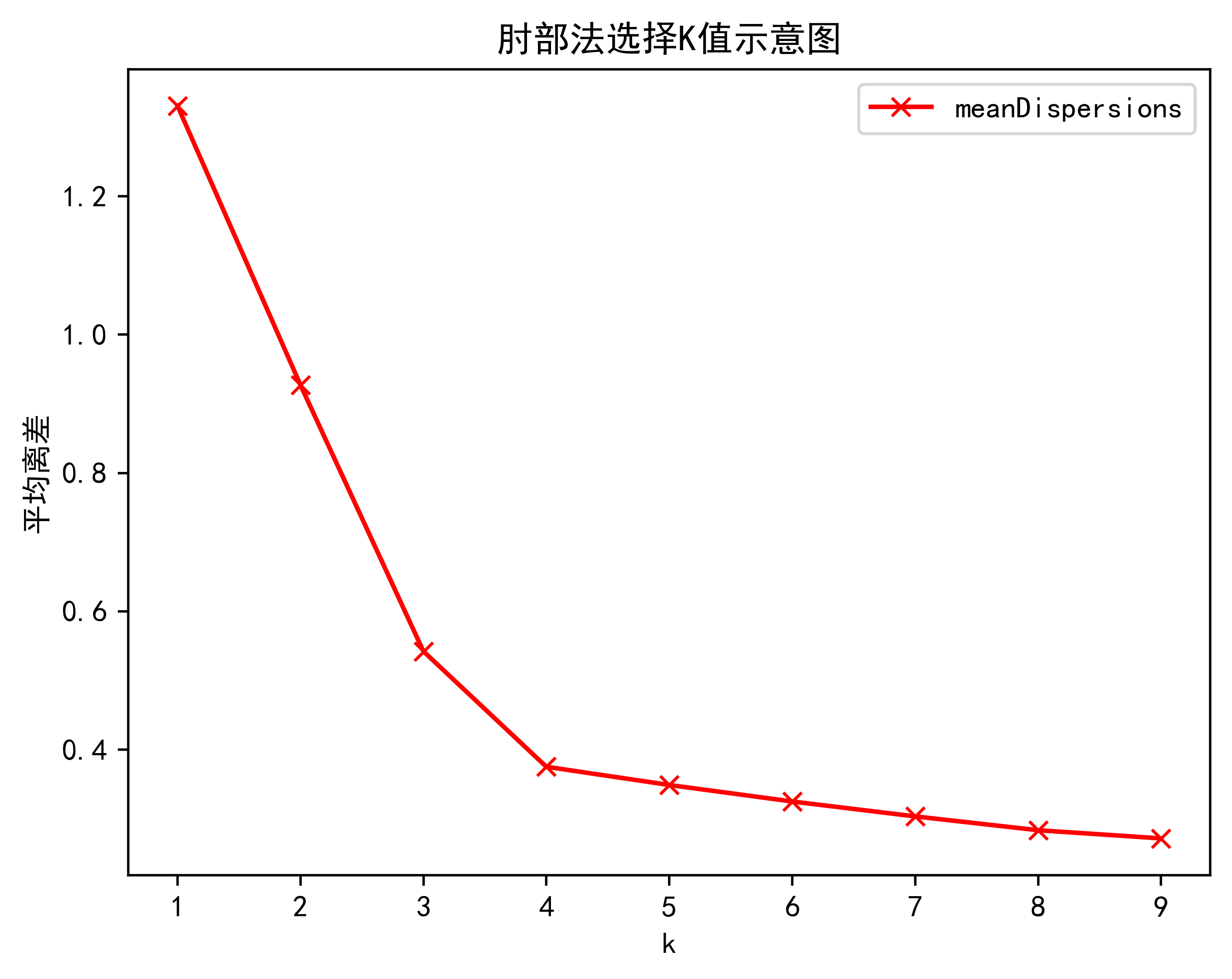
3.2.肘部法算法效果展示
1.算法流程简介
#k-means聚类方法
"""
k-means聚类算法流程:
1.K-mean均值聚类的方法就是先随机选择k个对象作为初始聚类中心.
2.这个时候你去计算剩余的对象于哪一个聚类中心的距离是最小的,优先分配给最近的聚类中心.
3.分配后,原先的聚类中心和分配给它们的对象就又会被看作一个新聚类.
4.每次进行分配之后,聚类中心又会被重新计算一次
5.直到满足某些终止条件为止:1.没有聚类中心被分配 2.达到了局部的聚类均方误差最小
"""2.1.K-mean算法核心代码
#%%
#1.当k已知且k=4时,我们执行k-means算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #散点图标签可以显示中文
#人为大致创建一个比较明显的聚类样本
c1x=np.random.uniform(0.5,1.5,(1,200))
c1y=np.random.uniform(0.5,1.5,(1,200))
c2x=np.random.uniform(3.5,4.5,(1,200))
c2y=np.random.uniform(3.5,4.5,(1,200))
c3x=np.random.uniform(2.5,3.5,(1,200))
c3y=np.random.uniform(2.5,3.5,(1,200))
c4x=np.random.uniform(1.5,2.5,(1,200))
c4y=np.random.uniform(1.5,2.5,(1,200))
x=np.hstack((c1x,c2x,c3x,c4x))
y=np.hstack((c2y,c2y,c3y,c4y))
X=np.vstack((x,y)).T
#n_cluster设置成4(可以修改)
kemans=KMeans(n_clusters=4)
result=kemans.fit_predict(X) #训练及预测
for i in range(len(result)):print("第{}个点:({})的分类结果为:{}".format(i+1,X[i],result[i]))
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='*',cmap='rainbow',s=9)
plt.xlabel('x')
plt.ylabel('y')
plt.title("K-means聚类效果图",color='black')
plt.savefig('C:\\Users\\Zeng Zhong Yan\\Desktop\\K-means聚类效果图.png', dpi=500, bbox_inches='tight')
plt.show()2.2.K-mean算法效果展示
3.1.肘部法算法核心代码
#%%
#2.如果k未知的情况下,利用肘部法来求出最优的k
"""
肘部法也非常简答,就是假设k=1-9,分别求出k=1-9之间的平均离差.
绘图观察最陡峭/斜率变化最大的点就是最为合适的k值
"""import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #使折线图显示中文K=range(1,10)
meanDispersions=[]
for k in K:#假设n_clusters=k,进行聚类后kemans=KMeans(n_clusters=k)kemans.fit(X)#计算平均离差m_Disp=sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0]meanDispersions.append(m_Disp)
result=[]
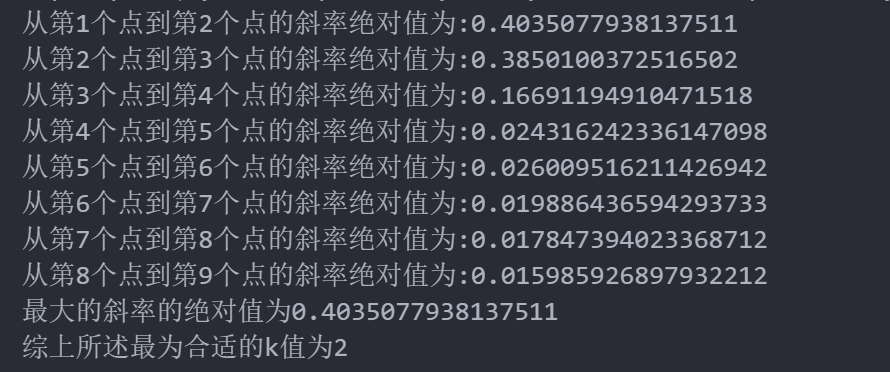
for i in range(len(meanDispersions)-1):print("从第{}个点到第{}个点的斜率绝对值为:{}".format(i+1,i+2,abs(meanDispersions[i+1]-meanDispersions[i])))result.append(abs(meanDispersions[i+1]-meanDispersions[i]))
#求解斜率最大值
result_max=max(result)
print("最大的斜率的绝对值为{}".format(result_max))
print("综上所述最为合适的k值为{}".format(result.index(result_max)+2))plt.plot(K,meanDispersions,'bx-',label='meanDispersions',color='red')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('肘部法选择K值示意图')
plt.legend()
plt.savefig('C:\\Users\\Zeng Zhong Yan\\Desktop\\肘部法求K值.png', dpi=500, bbox_inches='tight')
plt.show()3.2.肘部法算法效果展示











 的解决方法)
)






)