个人专栏—塑性力学

1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响
2.1 塑性力学——应力分析基本概念 应力分析基本概念
2.2 塑性力学——主应力、主方向、不变量 主应力、主方向、不变量

---

---

$斜截面上的应力$

• 主平面（Principal Plane） :剪应力为0的截面。

• 主单元体（Principal Body） :各侧面上剪应力均为0的单元体。

• 主应力（Principal Stress） :主平面上的正应力。

取四面体单元体微元进行应力分析,斜面外法线$\mathbf{N} $的方向余弦为 $l_x,l_y,l_z$,应力$\mathbf{P}$沿笛卡尔坐标系分量为 $p_x,p_y,p_z $.

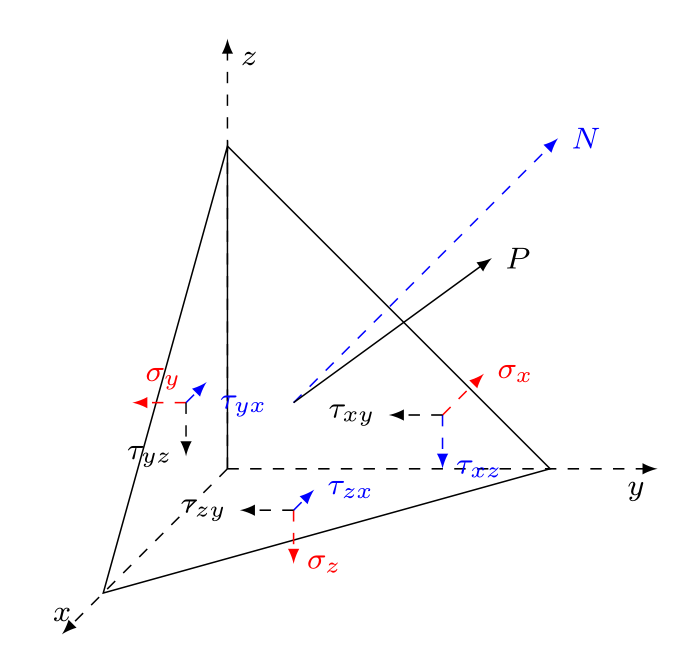
由弹性力学平衡方程可得斜面应力分量：
$$\begin{array}{c}\{\begin{array}{l}{p}_x={\sigma }_x{l}_x+{\tau }_{xy}{l}_y+{\tau }_{xz}{l}_z\\ p_y={\tau }_{yx}{l}_x+{\sigma }_y{l}_y+{\tau }_{yz}{l}_z\\ p_z={\tau }_{zx}{l}_x+{\tau }_{zy}{l}_y+{\sigma }_z{l}_z\end{array}\to p_i={\sigma }_{ij}{l}_j\end{array}$$

• 斜面总应力：
  $$\mathbf{P}=\sqrt{p_x^2+p_y^2+p_z^2}$$

• 斜面上的正应力：$\mathbf{P} $沿外法线方向的分量
  $${\sigma }_N=p_x{l}_x+p_y{l}_y+p_z{l}_z=p_i{l}_i$$

• 斜面上的总剪应力：
  $${\tau }_N=\sqrt{{\mathbf{P}}^2-{\sigma }_N^2}$$

当外法线 $\mathbf{N} $方向沿着主方向，则该面上剪应力为0，只有正应力，且正应力为 $\mathbf{P} $,设 $\mathbf{P} $大小为 $\lambda $,在各坐标轴投影为 $p_i=\lambda l_i $

$$\begin{array}{rl}& \{\begin{array}{l}{p}_i={\sigma }_{ij}{l}_j\\ p_i=\lambda l_i\end{array}\to ({\sigma }_{ij}-\lambda {\delta }_{ij})l_j=0\to {\sigma }_{ij}-\lambda {\delta }_{ij}|=0\\ & p_i={\sigma }_{ij}{l}_j\to \{\begin{array}{l}{p}_1={\sigma }_{11}{l}_1+{\tau }_{12}{l}_2+{\tau }_{13}{l}_3\\ p_2={\tau }_{21}{l}_1+{\sigma }_{22}{l}_2+{\tau }_{23}{l}_3\\ p_3={\tau }_{31}{l}_1+{\tau }_{32}{l}_2+{\sigma }_{33}{l}_3\end{array}\\ & p_i=\lambda l_i\to \{\begin{array}{l}{p}_1=l_1{\sigma }_N\\ p_2=l_2{\sigma }_N\\ p_3=l_3{\sigma }_N\end{array}\\ & \{\begin{array}{l}{l}_1({\sigma }_{11}-\lambda )+{\tau }_{12}{l}_2+{\tau }_{13}{l}_3=0\\ {\tau }_{21}{l}_1+l_2({\sigma }_{22}-\lambda )+{\tau }_{23}{l}_3=0\\ {\tau }_{31}{l}_1+{\tau }_{32}{l}_2+l_3({\sigma }_{33}-\lambda )=0\end{array}\to ({\sigma }_{ij}-\lambda {\delta }_{ij})l_j=0\\ & \left|\begin{array}{ccc}{\sigma }_{11}-\lambda & {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_{22}-\lambda & {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_{33}-\lambda \end{array}\right|=0\\ \to & {\lambda }^3-J_1{\lambda }^2+J_2\lambda -J_3=0\end{array}$$

求解三次方程：${\lambda }^3-J_1{\lambda }^2+J_2\lambda -J_3=0$可得$J_1,J_2,J_3$

$应力张量的三个不变量$

• 应力张量第一不变量
  $$J_1={\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}={\sigma }_{ii}$$

• 应力张量第二不变量
  $$J_2={\sigma }_{11}{\sigma }_{22}+{\sigma }_{22}{\sigma }_{33}+{\sigma }_{33}{\sigma }_{11}-({\sigma }_{12}^2+{\sigma }_{23}^2+{\sigma }_{31}^2)=\frac{1}{2}({\sigma }_{ii}{\sigma }_{kk}-{\sigma }_{ij}{\sigma }_{ji})$$

• 应力张量第三不变量
  $$J_3={\sigma }_{11}{\sigma }_{22}{\sigma }_{33}+2{\sigma }_{12}{\sigma }_{23}{\sigma }_{31}-{\sigma }_{11}{\sigma }_{23}^2-{\sigma }_{22}{\sigma }_{31}^2-{\sigma }_{33}{\sigma }_{12}^2=|{\sigma }_{ij}|=det({\sigma }_{ij})$$

• 主应力表示应力不变量
  $$\{\begin{array}{l}{J}_1={\sigma }_1+{\sigma }_2+{\sigma }_3\\ J_2={\sigma }_1{\sigma }_2+{\sigma }_2{\sigma }_3+{\sigma }_3{\sigma }_1\\ J_3={\sigma }_1{\sigma }_2{\sigma }_3\end{array}$$

$J_1,J_2,J_3 $取值与坐标轴的取向无关，称为应力张量的三个不变量。

$应力偏张量的三个不变量$

$$\begin{array}{c}{S}_{ij}=\left[\begin{array}{ccc}{\sigma }_x-{\sigma }_m& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y-{\sigma }_m& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z-{\sigma }_m\end{array}\right]=\left[\begin{array}{ccc}{S}_{11}& S_{12}& S_{13}\\ S_{21}& S_{22}& S_{23}\\ S_{31}& S_{32}& S_{33}\end{array}\right]\\ ⟹{\sigma }_{ij}-{\sigma }_m{\delta }_{ij}\to (S_{ij}-S_N{\delta }_{ij})l_j=0\end{array}$$

同理求解三次方程：$(S_{ij}-S_N{\delta }_{ij})l_j=0$

• 应力偏张量第一不变量
  $$J_1^{{}^{\prime }}=S_{11}+S_{22}+S_{33}={\sigma }_1+{\sigma }_2+{\sigma }_3-3{\sigma }_m=0$$

• 应力偏张量第二不变量
  $$\begin{array}{c}{J}_2^{{}^{\prime }}=-\frac{1}{2}{S}_{ij}{S}_{ji}=-\frac{1}{2}(2S_{12}^2+2S_{23}^2+2S_{31}^2+S_{11}^2+S_{22}^2+S_{33}^2)\\ \because 0=(S_{11}+S_{22}+S_{33}{)}^2=S_{11}^2+S_{22}^2+S_{33}^2+2S_{11}{S}_{22}+2S_{22}{S}_{33}+2S_{33}{S}_{11}\\ \to S_{11}^2+S_{22}^2+S_{33}^2=-(2S_{11}{S}_{22}+2S_{22}{S}_{33}+2S_{33}{S}_{11})\end{array}$$

$$\begin{array}{rl}{J}_2^{{}^{\prime }}& =-\frac{1}{2}(S_{11}^2+S_{22}^2+S_{33}^2)-S_{12}^2-S_{23}^2-S_{31}^2\\ & =-\frac{1}{6}(2(S_{11}^2+S_{22}^2+S_{33}^2)-2S_{11}{S}_{22}+2S_{22}{S}_{33}+2S_{33}{S}_{11})-S_{12}^2-S_{23}^2-S_{31}^2\\ & =-\frac{1}{6}[(S_{11}-S_{22}{)}^2+(S_{22}-S_{33}{)}^2+(S_{33}-S_{11}{)}^2]-S_{12}^2-S_{23}^2-S_{31}^2\\ & =-\frac{1}{6}[({\sigma }_x-{\sigma }_y{)}^2+({\sigma }_y-{\sigma }_z{)}^2+({\sigma }_z-{\sigma }_x{)}^2+6({\tau }_{xy}^2+{\tau }_{yz}^2+{\tau }_{zx}^2)]\\ & =\underset{\text{主轴方向}}{\underbrace{-\frac{1}{6}[({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_2-{\sigma }_3{)}^2+({\sigma }_3-{\sigma }_1{)}^2]}}\end{array}$$

• 应力偏张量第三不变量
  $$\begin{array}{rl}{J}_3^{{}^{\prime }}& =\frac{1}{3}{S}_{ij}{S}_{jk}{S}_{kl}\\ & =S_{11}{S}_{22}{S}_{33}+2S_{12}{S}_{23}{S}_{31}-S_{11}{S}_{23}^2-S_{22}{S}_{31}^2-S_{33}{S}_{12}^2\\ & =\underset{\text{主轴方向}}{\underbrace{S_{11}{S}_{22}{S}_{33}}}\end{array}$$

---

承接DIC数据图像处理模拟散斑制作（斑点直径≥0.1mm）及DIC散斑图像代处理：

如果你喜欢以上内容，或者对塑性力学感兴趣，欢迎一键三连，博主将持续更新，如果有任何问题，可以咨询博主，非常乐意为大家解答。