谷歌团队在17年的神作，论文17年6月发布 https://arxiv.org/abs/1706.03762 被NIPS2017收录，目前引用量已经逼近3w。
以下内容参考李沐老师的课程《动⼿学深度学习(Pytorch版)》

简介

• 注意力
  • 自主性：有目的的搜索某样东西（键）
  • 非自住性：无目的的关注某样东西（值）
    两种注意力机制的关系如下图所示：
    

多头注意力

模型
数学表示：
给定查询$q\in R^{d_q}$、$键k\in R^{d_k}$和值$v\in R^{d_v}$，每个注意⼒头hi（i = 1; : : : ; h）的计算⽅法为：

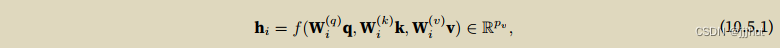
多头注意⼒的输出需要经过另⼀个线性转换，它对应着h个头连结后的结果，可学习的参数为$W_o$

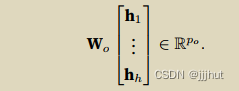
缩放点积注意力

使⽤点积可以得到计算效率更⾼的评分函数，但是点积操作要求查询和键具有相同的⻓度d。假设查询和键
的所有元素都是独⽴的随机变量，并且都满⾜零均值和单位⽅差，那么两个向量的点积的均值为0，⽅差为d。
为确保⽆论向量⻓度如何，点积的⽅差在不考虑向量⻓度的情况下仍然是1，我们再将点积除以pd，则缩放
点积注意⼒（scaled dot-product attention）评分函数为：
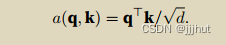在实践中，我们通常从⼩批量的⻆度来考虑提⾼效率，

自注意力

特点：查询、键和值来⾃同⼀组输⼊。
给定⼀个由词元组成的输⼊序列x1,…,xn，其中任意xi ∈Rd（1 ≤ i ≤ n）。该序列的⾃注意⼒输出为⼀个⻓
度相同的序列 y1,…,yn，其中：

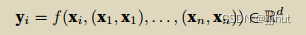
Compare CNN， RNN，Self-Attention

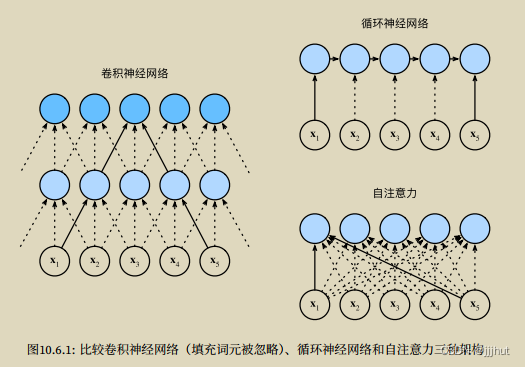
卷积神经⽹络和⾃注意⼒都拥有并⾏计算的优势，⽽且⾃注意⼒的最⼤路径⻓度最短。但是因为
其计算复杂度是关于序列⻓度的⼆次⽅，所以在很⻓的序列中计算会⾮常慢。

位置编码

在处理词元序列时，循环神经⽹络是逐个的重复地处理词元的，⽽⾃注意⼒则因为并⾏计算⽽放弃了顺序操
作。为了使⽤序列的顺序信息，通过在输⼊表⽰中添加 位置编码（positional encoding）来注⼊绝对的或相
对的位置信息。位置编码可以通过学习得到也可以直接固定得到。

• 基于正弦和余弦的位置编码：假设输⼊表示$X\in R^{n\times d}$ 包含⼀个序列中n个词元的d维嵌⼊表⽰。位置编码使⽤相同形状的位置嵌⼊矩阵$P\in R^{n\times d}$输出X + P，矩阵第i⾏、第2j列和2j + 1列上的元素为：
  

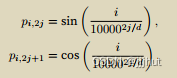
Transformer 结构

Transformer属于编码器－解码器架构的一种.
Transformer的编码器和解码器是基于⾃注意⼒的模块叠加⽽成的，源（输⼊）序列和⽬标（输出）序列的嵌⼊（embedding）表⽰将加上位置编码（positional encoding），再分别输⼊到编码器和解码器中。
Transformer 结构如下图所示：

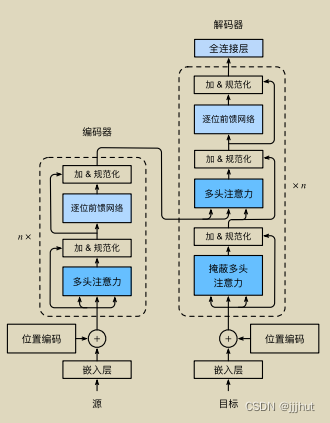
Transformer架构如上图所示，是一个seq2seq model，左半边是encoder，右半边是decoder。Transformer的编码器和解码器都堆叠了6层，n=6 。encoder的输入是一个sequence，经过Multi-Head Attention之后得到另一个sequence，Add&Norm包括一个残差连接和Layer Normalization
decoder的输入是前一个time step的output，Masked Multi-Head Attention是指attention只能作用在已经产生的输出上，第二个Multi-Head Attention会attention到encoder的输出。

Transformer 训练阶段

在训练阶段，首先需要获取数据及其标签，例如一定声音讯号，对应的标签是“机器学习”，声音讯号作为encoder的输入，而decoder在训练阶 段的输入是正确标签，即“机器学习”（因此需要masked multi-head attention），我们希望decoder的输出尽可能接近真实标签，最小化交叉熵

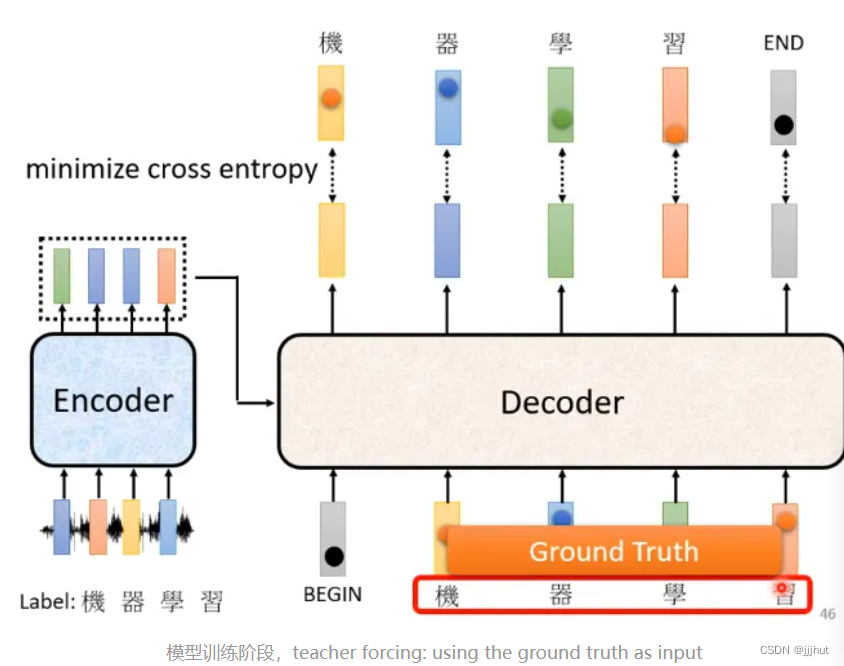
在预测阶段，decoder看不到真实标签，看到的是自己的输入，因此这里有一个mismatch，叫做exposure bias，一个解决方案是在训练阶段给decoder一些错误的输入，增加模型的鲁棒性，这种方法叫做scheduled sampling