系统定义
系统:指若干相互关联的事物组合而成的具有特定功能的整体。
系统的基本作用:对输入信号进行加工和处理,将其转换为所需要的输出信号。
系统分类
系统的分类错综复杂,主要考虑其数学模型的差异来划分不同类型。主要分为:线性与非线性、即时与动态(记忆)、时变与时不变、因果与非因果等。
1、连续时间系统与离散时间系统
连续时间系统:系统的输入和输出都是连续时间信号,且内部也未转换为离散时间信号,则称此系统为连续时间系统。其数学模型为微分方程。
离散时间系统:若系统输入输出都是离散时间信号,则称此系统为离散时间系统。其数学模型为差分方程。
混合系统:实际上,离散时间系统经常与连续时间系统组合运用,此情况称为混合系统。
2、线性系统与非线性系统
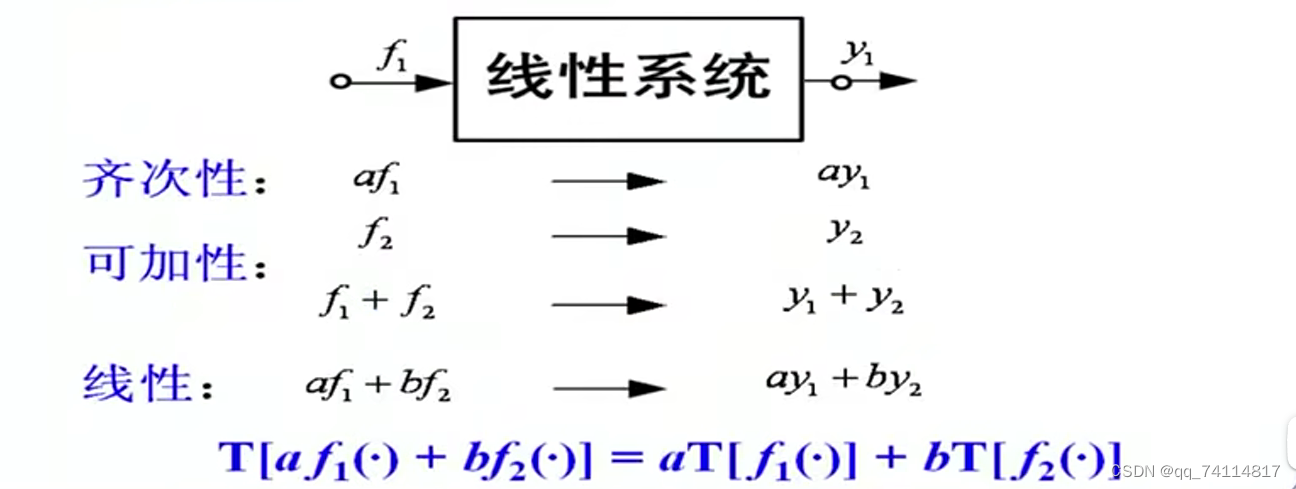
线性系统:指满足线性性质(齐次性、可加性)的系统。不满足齐次性或可加性的系统为非线性系统。
齐次性也称为均匀性,可加性也称为叠加性。
3、时变系统与时不变系统
时不变系统:系统输入延迟多少时间,零状态响应也响应延迟多少时间。也称为非时变系统、定常系统。(郑君里老师版本:系统参数不随时间而变化)
时变系统:系统的参数随时间而改变,则称其为时变系统(参变系统)。
4、即时系统与动态系统
动态系统:响应不仅与激励有关,还与它过去的状态
有关。含记忆元件(电容、电感)的系统为动态系统,否则为即时系统。
当动态系统满足以下三个条件时,为线性系统:
5、因果系统与非因果系统
因果系统:指系统在t0时刻的响应只与t=t0和t<t0时刻的输入有关。否则为非因果系统。
也就是说系统的输出仅与当前或过去的输入有关,而与将来的输入无关的系统。因此,因果系统是“物理可实现的”。
6、其他系统
集总参数系统与分布参数系统、可逆系统与不可逆系统等。
线性时不变系统
重点讨论确定性输入信号作用下的集总参数线性时不变系统。一般简称LTI系统。
线性时不变系统的基本性质:

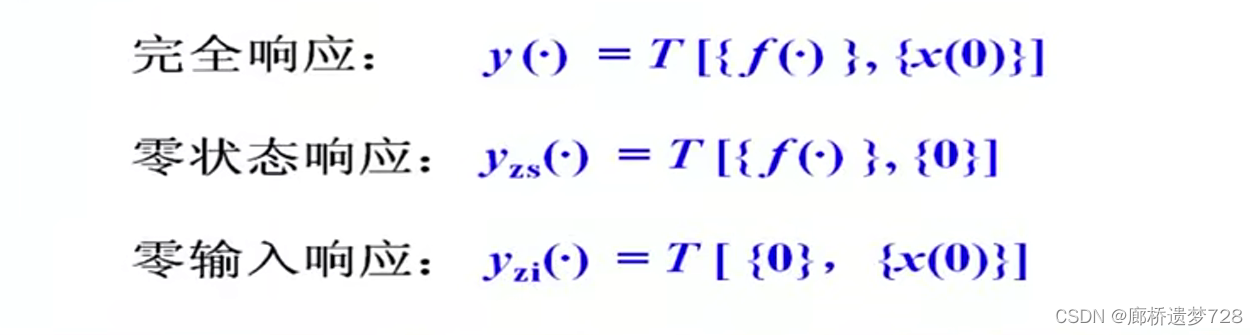
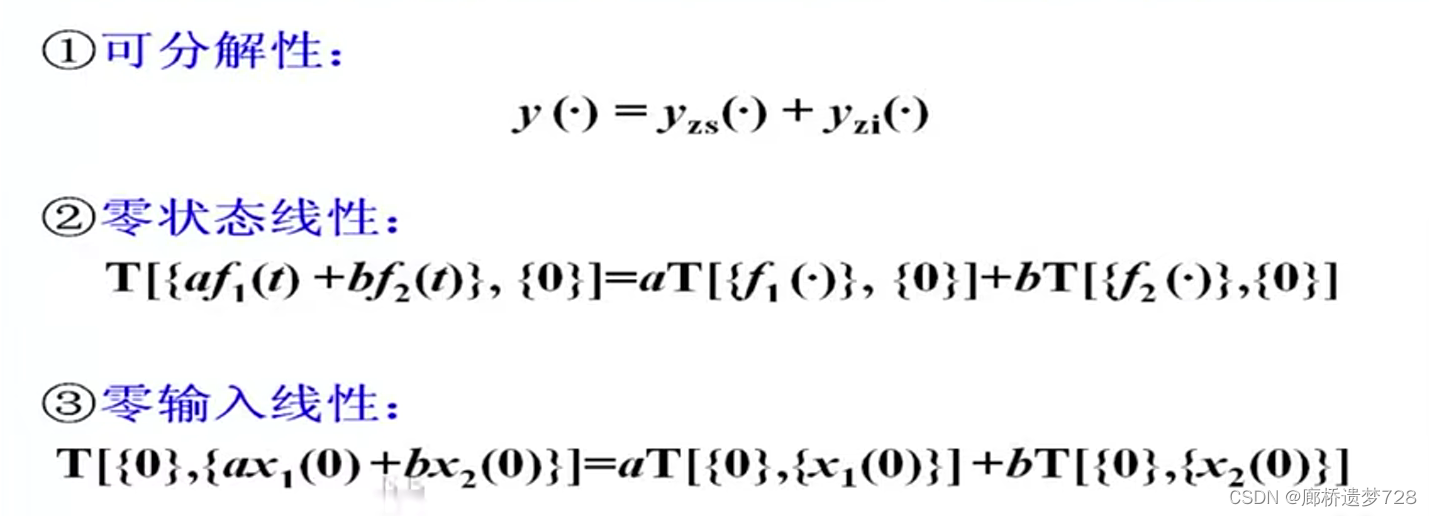






)














