算法学习11：树与图的 DFS、BFS

文章目录

算法学习11：树与图的 DFS、BFS
前言
一、树与图的深度优先遍历
- 1.例题：树的重心：
二、树与图的宽度优先遍历
- 1.例题：图中点的层次：
三、拓扑排序：（入度为0的点）
- 1.例题：有向图的拓扑排序：
总结

前言

在这里插入图片描述

提示：以下是本篇文章正文内容：

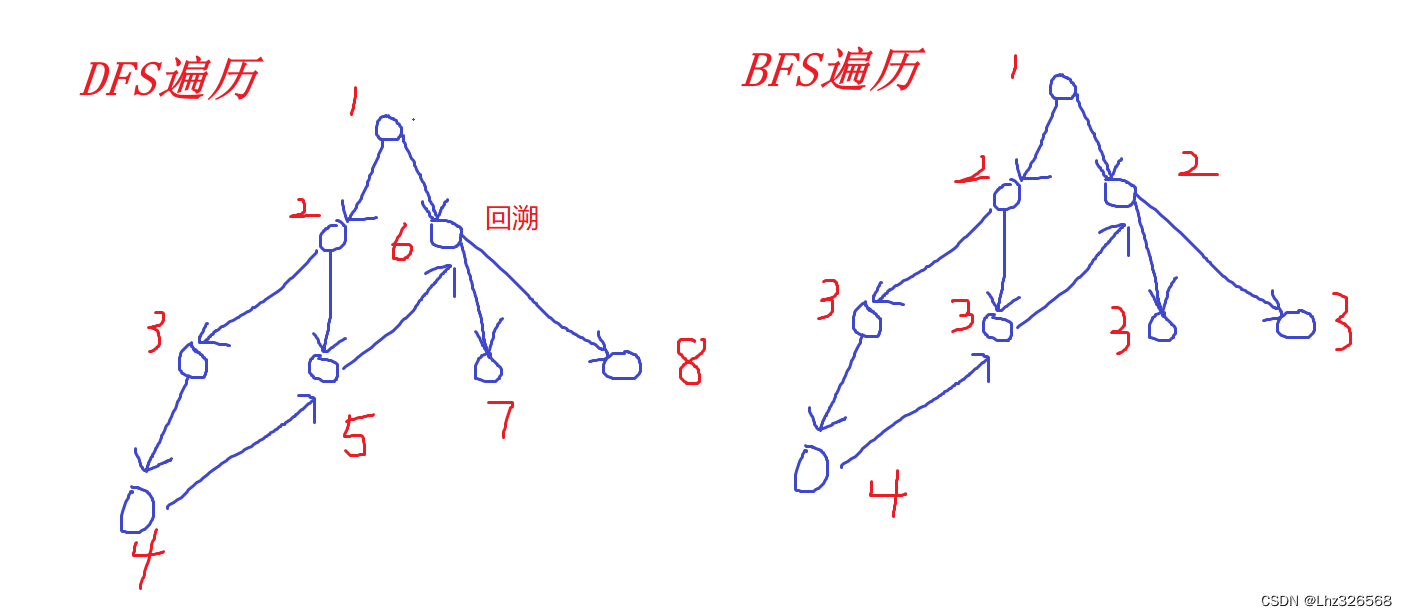
一、树与图的深度优先遍历

1.例题：树的重心：

例题1：给定一棵树，有n个结点（编号1~n）和n-1条无向边。
请找到树的重心，输出将重心删除后，剩余各个连通块中，点的数量的最大值。
重心定义：是树的结点，将这个点删除后，剩余的各个连通块中，点的数量的最大值最小。

// 分析1（另一种思路）：
// 先找重心：删除这个结点，剩余的点数最大值要最小。
// 再找此时的点数最大值。// 分析2（对的）：
// 找到删掉重心后点数的最大值，然后不断更新，从这些最大值中找最小的。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
// 1e5 是科学计数法表示10的5次方
const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;// idx：当前结点
bool st[N];// 标记结点是否被访问过 int ans = N;// 答案 // 在邻接表中插入元素：加一条单向边 
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;} // 以u结点为根，子节点的数量和
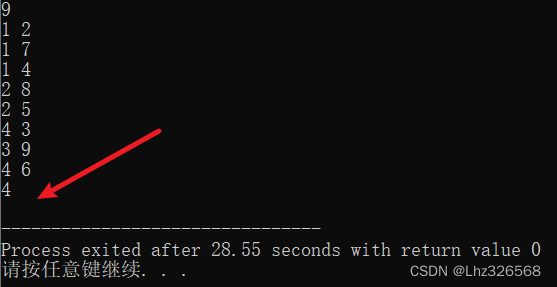
int dfs(int u){st[u] = true;// 标记一下，已经被搜过了// sum：以u结点为根，子节点的数量和// res：删掉重心后点数的最大值 int sum = 1, res = 0;// 遍历结点的邻接表  for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];// 结点 if(!st[j]){int s = dfs(j);res = max(res, s);// 子树的点数最大值 sum += s;}} // n - sum：(技巧)处理，请看图 res = max(res, n - sum);// 掉重心后点数的最大值 ans = min(ans, res);// 在“掉重心后点数的最大值”找最小的 return sum;} int main()
{cin >> n; memset(h, -1, sizeof h);// 全部置为-1 // 往邻接表里面插入n-1条边// 无向图就插入两次 for(int i = 0; i < n - 1; i ++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}

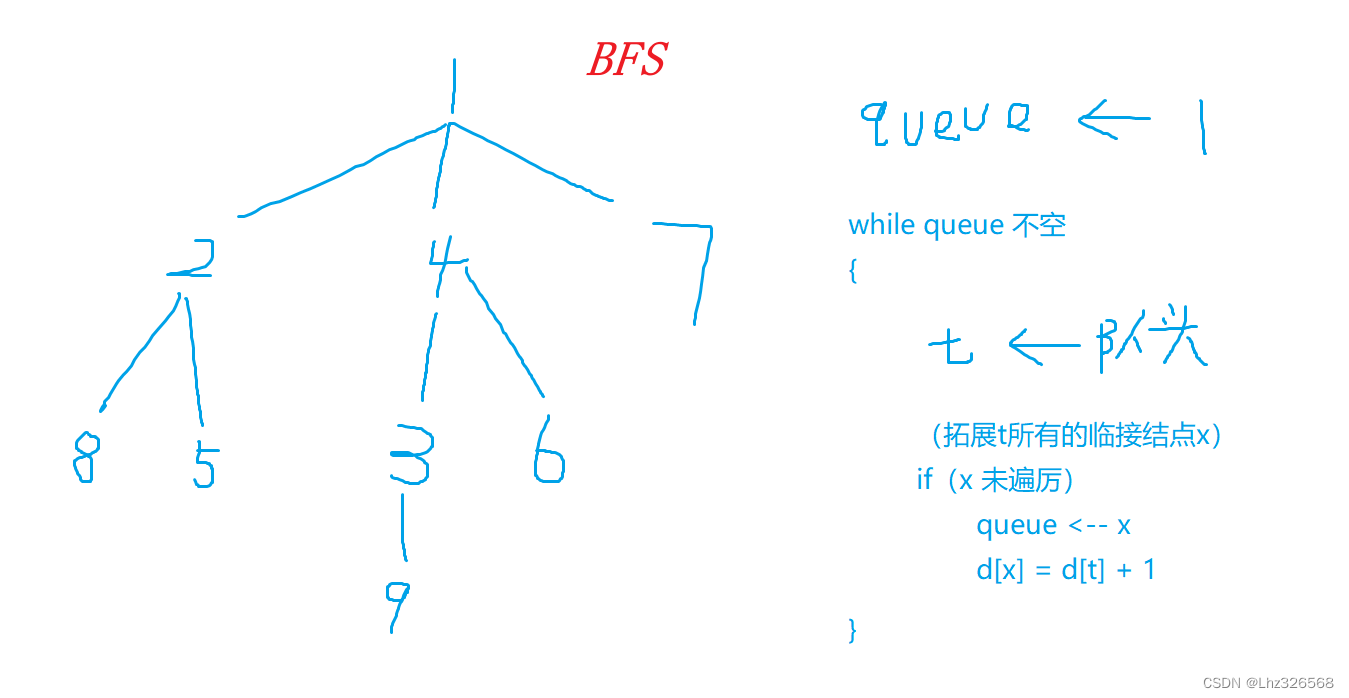
在这里插入图片描述

二、树与图的宽度优先遍历

1.例题：图中点的层次：

在这里插入图片描述

给定一个n个点，m条边，的“有向图”，图中可能存在“重边”和“自环”。
“所有的边长度为1”，点的编号是1~n。
请你求出1号点到n号点的最短距离，如果1号点无法走到n号点，输出-1.

#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;
// d：1号点到其他点的最短距离 q：队列 
int d[N], q[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}int bfs()
{int hh = 0, tt = 0;q[0] = 1;// 对头元素 memset(d, -1, sizeof d);d[1] = 0;// 根节点 while(hh <= tt)// 当对列不空 {int t = q[hh ++];// 取对头 for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];// 取邻接节点 if(d[j] == -1)// 未遍历过 {q[++ tt] = j;d[j] = d[t] + 1;}} } return d[n];// 1号点到n号点的最短距离
}int main()
{cin >> n >> m;// memset：member set memset(h, -1, sizeof h);for(int i = 0; i < m; i ++){int a, b;cin >> a >> b;add(a, b);}cout << bfs() << endl;return 0;}

在这里插入图片描述

三、拓扑排序：（入度为0的点）

1.例题：有向图的拓扑排序：

在这里插入图片描述

给定一个n个点，m条边的“有向图”，图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列，如果不存在，输出-1.
拓扑序列定义：对于每条边（x，y），x都出现在y之前

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;
// q：队列  d：入度 
int q[N], d[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;} bool topsort()
{int hh = 0, tt = -1;// 所有入度为0的点进入队列 for(int i = 1; i <= n; i ++)if(!d[i]) q[++ tt] = i;while(hh <= tt)// 当队列不空 {int t = q[hh ++];// 取对头 // 遍历邻接结点 for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];// 取结点j d[j]--;// j的入度-1 if(d[j]==0) q[++ tt] = j;// 入度为0，进队列 }}return tt == n - 1;// 判断队列里面的元素个数是否等于n 
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);// 给图加边 for(int i = 0; i < m; i ++){int a, b;cin >> a >> b;add(a, b);d[b] ++;// 计算入度 }if(topsort()){// 队列元素就是 “拓扑序” for(int i = 0; i < n; i ++) printf("%d ", q[i]);puts("");// 在末尾自动添加一个换行符// printf("\n"); } else puts("-1");return 0;
}