C语言：深入补码计算原理

- 有符号整数存储
- - 原码、反码、补码
  - - 转换规则
    - 数据与内存的关系
- 补码原理

有符号整数存储

原码、反码、补码

有符号整数的2进制表示方法有三种，即原码、反码和补码
三种表示方法均有符号位和数值位两部分，符号位用0表示“正”，用1表示“负”。

有符号整数最高位的一位是被当做符号位，剩余的都是数值位。
无符号整数所有的位都是数值位

转换规则

正整数：原、反、补码都相同。

负整数：
原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。
补码：反码+1就得到补码。

正数：

int a = 5;

对于int（整形），内存会开辟4个字节来存放a。由于a是正数，第一位符号位为0，数值为5，转化为二进制就是101，高位补0。正数的原反补三码相同。
故：

a 的原码： 00000000 00000000 00000000 00000101
a 的反码： 00000000 00000000 00000000 00000101
a 的补码： 00000000 00000000 00000000 00000101

负数：

int b = -5;

由于在此b是负数，在原码中，第一位是符号位，存放1，表示负数。
反码：符号位不变，保持为1。其余位按位取反，即0变1，1变0.
补码：在反码的情况下加1。
故：

b 的原码： 10000000 00000000 00000000 00000101
b 的反码： 11111111 11111111 11111111 11111010
b 的补码： 11111111 11111111 11111111 11111011

而补码想要变回原码，也是相同的步骤，即先取反后加一。

数据与内存的关系

首先，我们在内存中存储的数据是以补码的形式存储的。我们用代码定义a，b为5和-5，然后观察其在内存中的值：
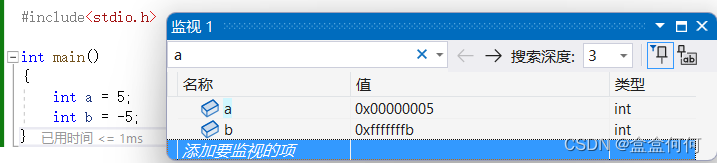
在这里插入图片描述
由于二进制实在难于分辨，可读性非常差，所以编译器在向程序员呈现计算机存储的值的时候，会转为16进制。我们从上图中可见，a的存储是0x00000005即16进制的5。可b的值却不是-00000005。这个fffffffb其实就是-5的补码 11111111 11111111 11111111 11111011的16进制形式，由此可以证明，内存存储有符号整数就是以补码的形式。

那为什么内存要存补码？

可以把符号与数值统一处理，把数字的正负放在码值中，不用额外区分。
可以使加法减法统一处理（CPU只有加法计算器）。

第一点其实是容易理解的，那为什么用补码可以统一加减法呢？我们以下面的代码为例：

int a = 3;
int b = 5;
int c = a - b;

在以上计算过程中，计算机会把3 - 5当作3 + (-5)，然后将两个数字的补码相加。

a 的补码： 00000000 00000000 00000000 00000011
b 的补码： 11111111 11111111 11111111 11111011
--------------------------------------------
两者相加： 11111111 11111111 11111111 11111110
上式取反： 10000000 00000000 00000000 00000001
上式加一： 10000000 00000000 00000000 00000010
最后得到的值即为-2

可以看到我们确实以加法的形式，完成了减法的计算。以上代码中，计算机想要完成3 - 5，于是CPU将其转化为了3 + (-5)，然后直接将补码相加，然后转回原码，得到的就是正确答案。

我们再来看到一个案例：

int a = 10;
int b = 5;
int c = a - b;

在以上计算过程中，计算机会把10 - 5当作10 + (-5)，然后将两个数字的补码相加。

a 的补码： 00000000 00000000 00000000 00001010
b 的补码： 11111111 11111111 11111111 11111011
--------------------------------------------
两者相加： 1 00000000 00000000 00000000 00000101

此时出现了一个问题，那就是进位导致的位数溢出，由于int类型只能存储32位数据，此时超出的数据就会被丢弃。
所以计算后实际值是： 00000000 00000000 00000000 00000101也就是5，我们再次完成了计算。

可见，虽然代码是减法，但是在计算机处理的时候，只做了加法运算。这样可以减少计算机硬件的消耗，只需要在CPU内部做好加法的硬件即可。

本博客还要继续探讨，为什么计算机可以通过补码计算统一加减法。

补码原理

现在假设我们有一个十进制计算机，每个bit位可以存储0 - 9十种数据，现在我们有一个可以存储4位数据内存，接下来我们要完成一个计算：

求出50 - 19的结果：

值得注意的是：由于我们只能存储4位数据，所以如果我们计算中发生了溢出，多出来的位要舍弃。

50 的存储：0050
19的存储：0019

接下来我们进行计算：

50 - 19
= 50 + (-19)
= 50 + (-19) + 9999 + 1 - 10000

到这一步，我暂时停止了，因为我要重复申明刚刚的规则：计算中发生了溢出，多出来的位要舍弃。

由于计算机只能存储四位，而计算机是一步一步进行计算的，所以中间的每一个变量都要保存下来，而在保存10000时，我们的位数溢出了，要舍弃高位的1，于是上述计算变为：

= 50 + (9999 - 19) + 1 - 0000
= 50 + (9999 - 19 + 1)
= 50 + 9981
= 10031

由于计算机只能存储四位，而在保存10031时，我们的位数溢出了，舍弃高位的1，于是上述计算变为：

= 0031
= 31

而50 - 19结果就是31，整个计算过程看起来非常怪异，为什么还能得到正确结果？？？

首先，我们要计算的是一个减法 50 - 19，于是我把它转化为了加法50 + (-19)，但是这依然改变不了它需要进行相减的本质，我们有没有办法把-19转化为一个正数x，让50 + x == 50 + (-19)？

在数学界，这就是异想天开，但是我们的数据是存在计算机中的，其实是有可能实现的，而实现它的本质，就在于丢弃溢出位数的功能。

数学角度，10000 + (-19) + 50等于10031，但是从这个只能存四位的内存的角度，10031就是31。也就是说，我们可以给一个负数加上刚好到溢出位数的数字，故意让其溢出，这样就可以50 + (10000 - 19) == 50 + (-19)了。

但是这涉及到一个问题：根本没有四位的内存可以存下10000这个数据，那就更无法在计算机中完成10000 + (-19)了。于是我们将10000拆分为两个4位以内的数字9999 和 1，让10000 + (-19)变成9999 + 1 + (-19)，这就是计算机可以执行的了。这样你也许就可以看懂以上的算式了。

接下来，我们要把上面的溢出效果带入到一般的二进制计算机中：

现在我们要完成减法：5 - 3，数据都以int类型存储：

那么我们就要先将上式转化为5 + (-3)，接着对-3进行一次溢出的计算：

-3的二进制： -00000000 00000000 00000000 00000011（前面有负号）
加上一个刚好溢出的整数： 1 00000000 00000000 00000000 00000000
拆解出两个int可以存储的数字： 11111111 11111111 11111111 11111111 + 1
先让-3 + 11111111 11111111 11111111 11111111
结果：11111111 11111111 11111111 11111100
再+1：11111111 11111111 11111111 11111101

最后我们就可以拿11111111 11111111 11111111 11111101 代替-3进行计算了。
而中途有一个过程：

先让-3 + 11111111 11111111 11111111 11111111
结果：11111111 11111111 11111111 11111100

你有没有发现，这个结果11111111 11111111 11111111 11111100 刚好就是-3的每一位取反？
数学角度来说，-3 + 11111111 11111111 11111111 11111111 是要执行减法的，可是二进制中可以用每一位取反达到同样的效果，而对于计算机而言，对每一个bit位取反并不是什么难事。因此计算机的计算，就是在这一步把减法消除掉的。
其实这就是得到反码的过程，所以反码要求按位取反！

而最后一步