动态规划模型的要素是对问题解决的抽象,其可分为:
阶段。指对问题进行解决的自然划分。例如:在最短线路问题中,每进行走一步的决策就是一个阶段。
状态。指一个阶段开始时的自然状况。例如:在最短线路问题中,每进行走一步后,对所走的点进行标注。
决策。当一个阶段的状态确定后,作出选择从而演变到下一阶段的某个状态的选择手段称为决策,在优控制问题中也称为控制。
策略。由决策组成的序列称为策略。由第k到第j阶段的策略可记作
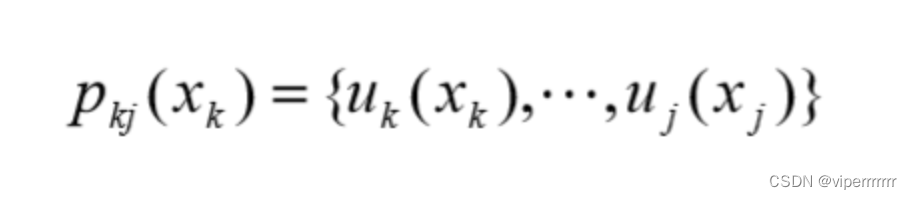
下面以我在建模美赛中的题目实列来阐述:
前面第一问得到了五大湖的最佳水位,第二问的核心是波动情况下,近可能地使得五大湖的最佳水位波动尽可能小。
采用之前构建的网络流模型来模拟五大湖及其连接河流的水位和流量:节点定义:将每个湖泊和与其直接相连的河流定义为网络中的一个节点。边定义:根据水流方向,定义从一个节点到另一个节点的边。
流量和水位数据准备:使用提供的平均水位和流量数据来设定节点属性和边的容量运用网络流算法来模拟水流动态,并应用目标优化方法寻找维持最佳水位的策略。不过我们只考虑河流影响因素,其它外部因素不考虑在内。
一、算法实现:
制定算法:遗传算法(GA):使用遗传算法等启发式算法求解优化问题,找到维持最优水位的控制策略。通过湖泊的流入和流出数据来维持五大湖的最佳水位。
解释:
遗传算法(Genetic Algorithm,简称GA)起源于对生物系统所进行的计算机模拟研究,是一种随机全局搜索优化方法,它模拟了自然选择和遗传中发生的复制、交叉(crossover)和变异(mutation)等现象,从任一初始种群(Population)出发,通过随机选择、交叉和变异操作,产生一群更适合环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代不断繁衍进化,最后收敛到一群最适应环境的个体(Individual),从而求得问题的优质解。
步骤如下:
在动态流模型中如果当前水位低于目标水位,减少流出量;反之增加流出量。不同的是遗传算法在本基础上加上往年同月或同季节中的河流量变化值作为参考,在该动态网络流模型中的再次进行相应的河流流量调整从而得到最后相对更加准确的结果。
采用简单遗传算法:
SGA=(C,E,P_0, M,D, H,S,T)
C 表示个体的编码方案
E 表示个体适应度评价函数
P_0 表示初始种群
M 表示种群
D表示选择算子
H表示交叉算子
S表示变异算子
T 表示遗传算法终止条件
遗传算法使用以下遗传算子:
从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体被选中的概率跟适应度值有关,个体适应度值越高,被选中的概率越大,根据该思想,建立河流流量概率相关值:
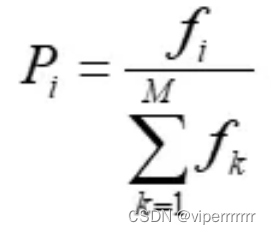
fi为本遗传值,叠加之后为累次遗传。
在此之后,再进行指数尺度变换:
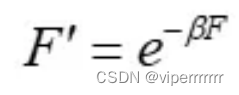
得到每个湖的在不同遗传系中的适配分部数据的热力图:
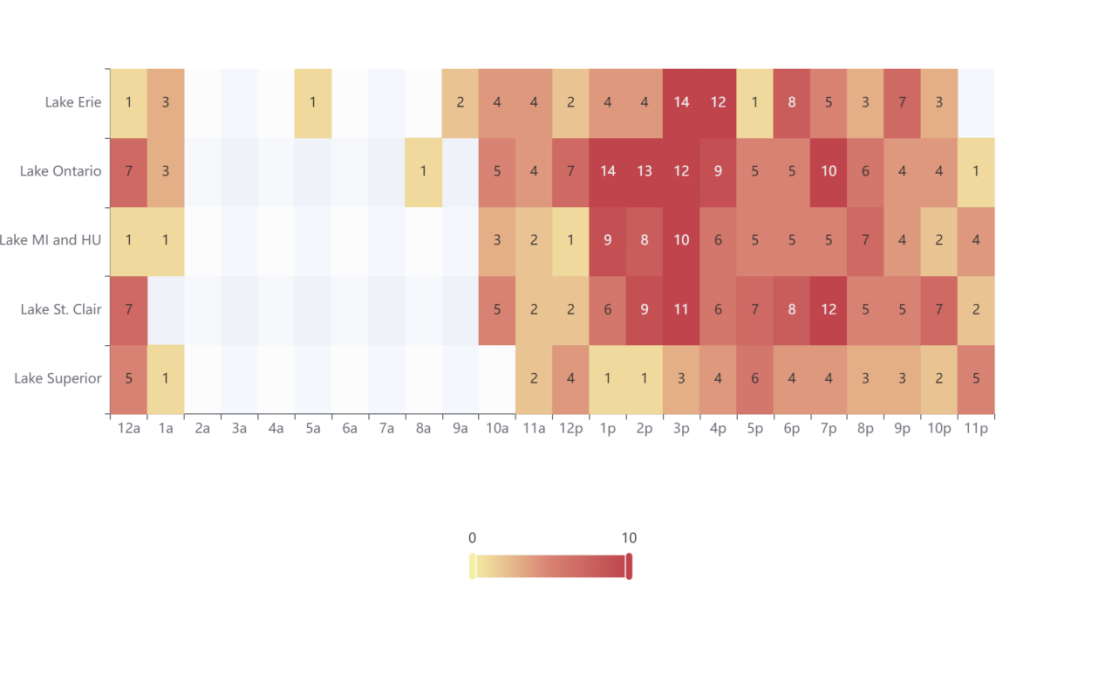
再通过动态网络流模型得到湖泊之间连接的河流流量的调整值:
圣玛丽河:2178.23
圣克莱尔河:5739.34
底特律河:5991.12
尼亚加拉河:6023.77



之查找算法2_BFS)





(31))









