EF类和E/F类功率放大器(能量转换器)的波形推导和理想仿真–基于Matlab和ADS
参考论文:Modeling and Analysis of Class EF and Class E/F Inverters With Series-Tuned Resonant Networks(2016)
这篇文章的思路和MTT的文章A Generalized High-Efficiency Broadband Class-E/F3 Power Amplifier Based on Design Space Expanding of Load Network还有CAS的文章Novel Design Space of Broadband High-Efficiency Parallel-Circuit Class-EF Power Amplifiers的底层理论是相似的。
全部工程下载(Matlab+ADS):EF类和E/F类的波形推导和理想电路仿真工程-基于Matlab和ADS
这个论文我当时手推非常慢,花了一周搞推导吧,搞了个基于Matlab的syms推出的解析表达式和分析流程
众所周期,EF类和E/F类都是混合的模式类型,EF是在E类的基础上控制了偶次谐波使其短路,E/F类是在E类的基础上控制奇次谐波短路。但是,EF类和E/F类都是有其对应的原始电路实现的,下面对Matlab推导和ADS验证过程进行介绍。
目录
- EF类和E/F类功率放大器(能量转换器)的波形推导和理想仿真--基于Matlab和ADS
- 1 、EF类和E/F类的简单理论
- 2 、使用MATLAB计算EF类和E/F类的波形与参数
- 3 、ADS的理想仿真
- 4 、EF类和E/F类的基于MATLAB推导过程
1 、EF类和E/F类的简单理论
尽管 E 类PA可以用相对简单的电路拓扑实现100%的理论效率,但它面临着高峰值开关电压的问题。将E类开关模式和谐波调谐技术相结合,可以得到 Class-EF 或 E/F 模式。经典的Class-EF与Class-E/F的电路图与其等效电路如下图所示:
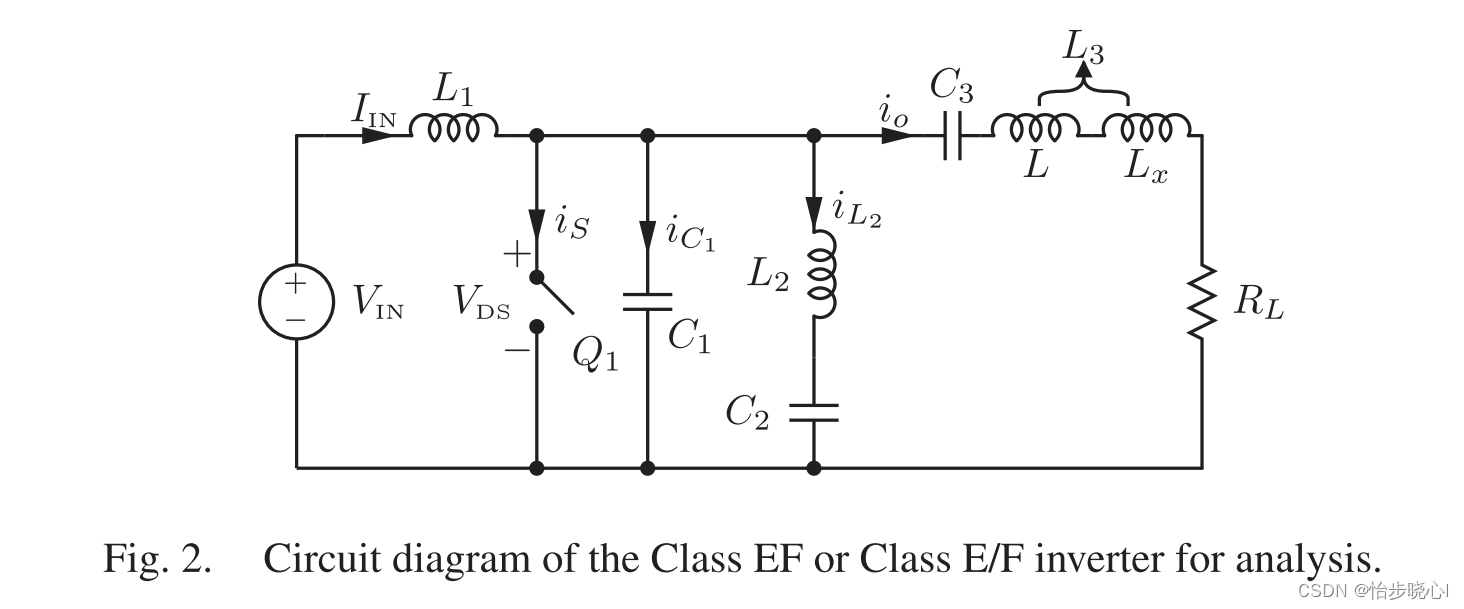
其中 L 1 L1 L1为射频扼流圈, C 1 C1 C1为并联电容, C 3 {C_3} C3和部分 L 3 {L_3} L3谐振在基频(和L谐振在基频), C 2 L 2 {C_2}{L_2} C2L2起到谐波调谐的作用。对于Class-EF类PA,其需要控制偶次谐波,因此n为偶数。类似的,对于Class-E/F类PA,其需要控制奇次谐波,因此n为奇数。
但是,虽然EF类和E/F类控制的谐波次数不同,但都需要满足ZVDS和ZVS条件,这也是推导的关键步骤之一。
但是,在开始推导之前,我们需要关注一些需要预先设置的变量。参考上面的论文,我们需要优先设置要控制的谐波次数q,占空比D,和电容C1与C2的比值 k = C 1 C 2 k=\frac{C_{1}}{C_{2}} k=C2C1。当然,这些参数也会影响波形:
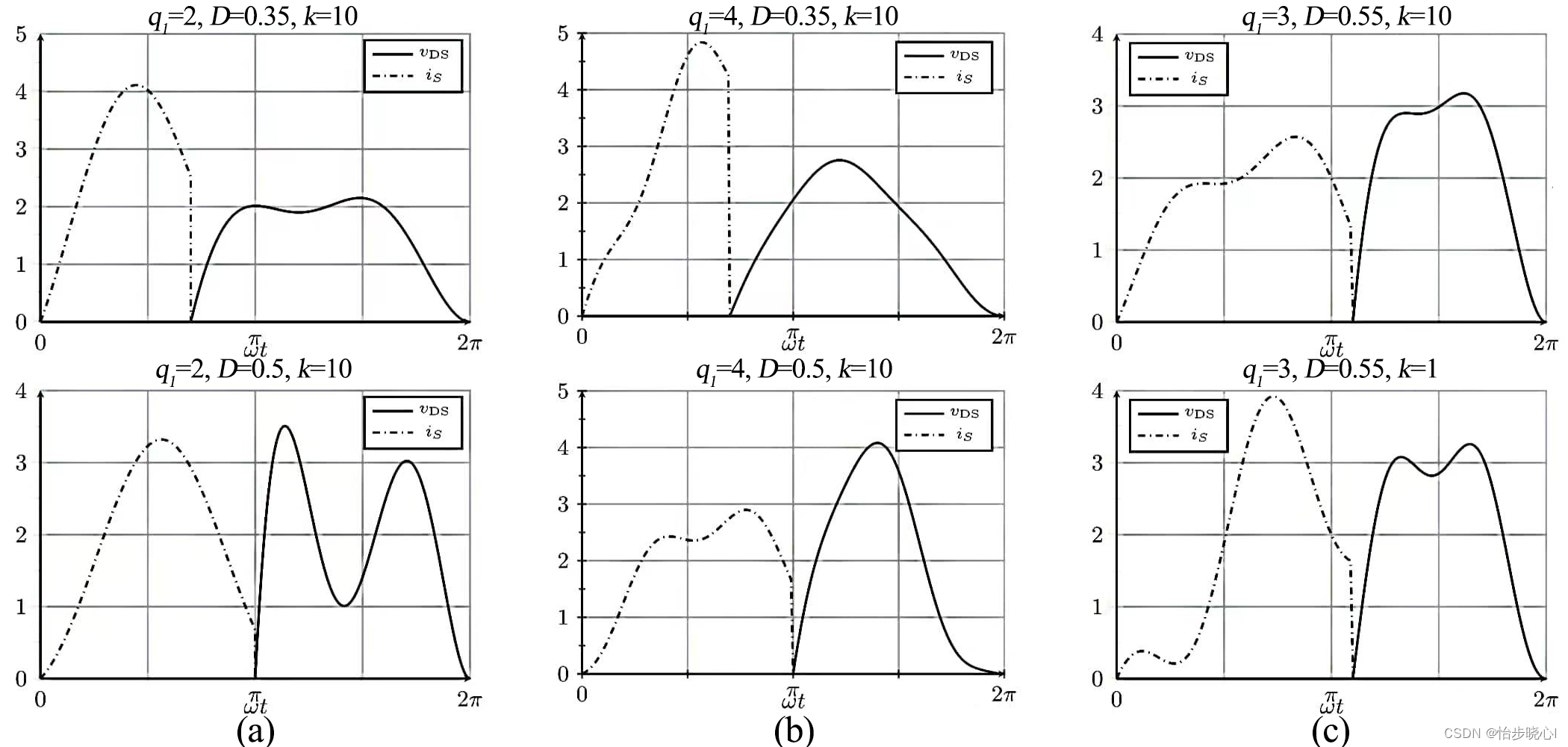
2 、使用MATLAB计算EF类和E/F类的波形与参数
main.m,运行前设置q,D,k参数!!!
这部分的推导参考 (4 、EF类和E/F类的推导过程),这边直接给出计算代码的效果。首先,我们需要确定的是设置要控制的谐波次数q,占空比D,和电容C1与C2的比值 k = C 1 C 2 k=\frac{C_{1}}{C_{2}} k=C2C1。此处以q=2,D=0.375,k=0.869为例,得到的结果为:
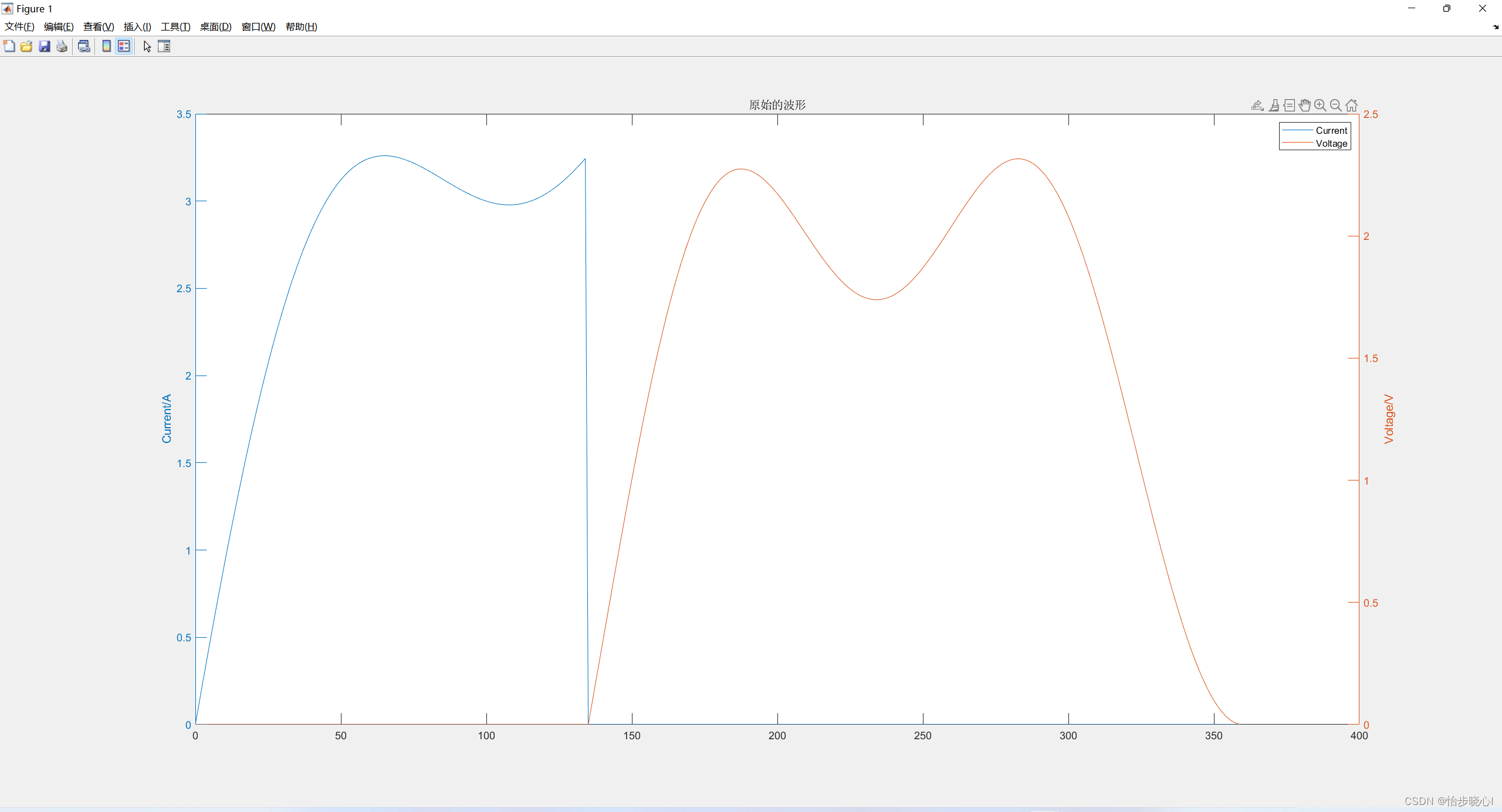
同时,命令行也会给出对应的设计参数,这些参数对应的是归一化电压和电流,也就是理想的输出功率为1W:
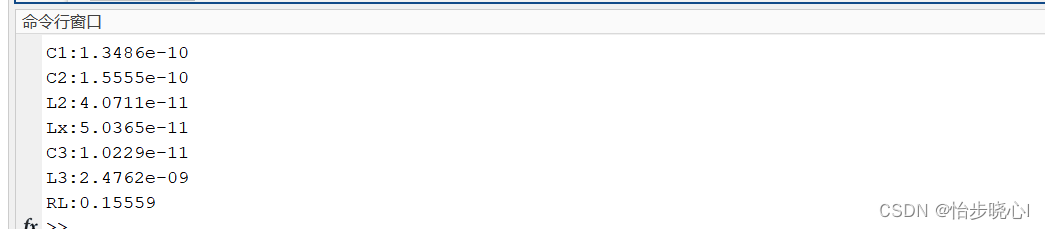
3 、ADS的理想仿真
使用上面的计算参数,q=2,D=0.375,k=0.869:
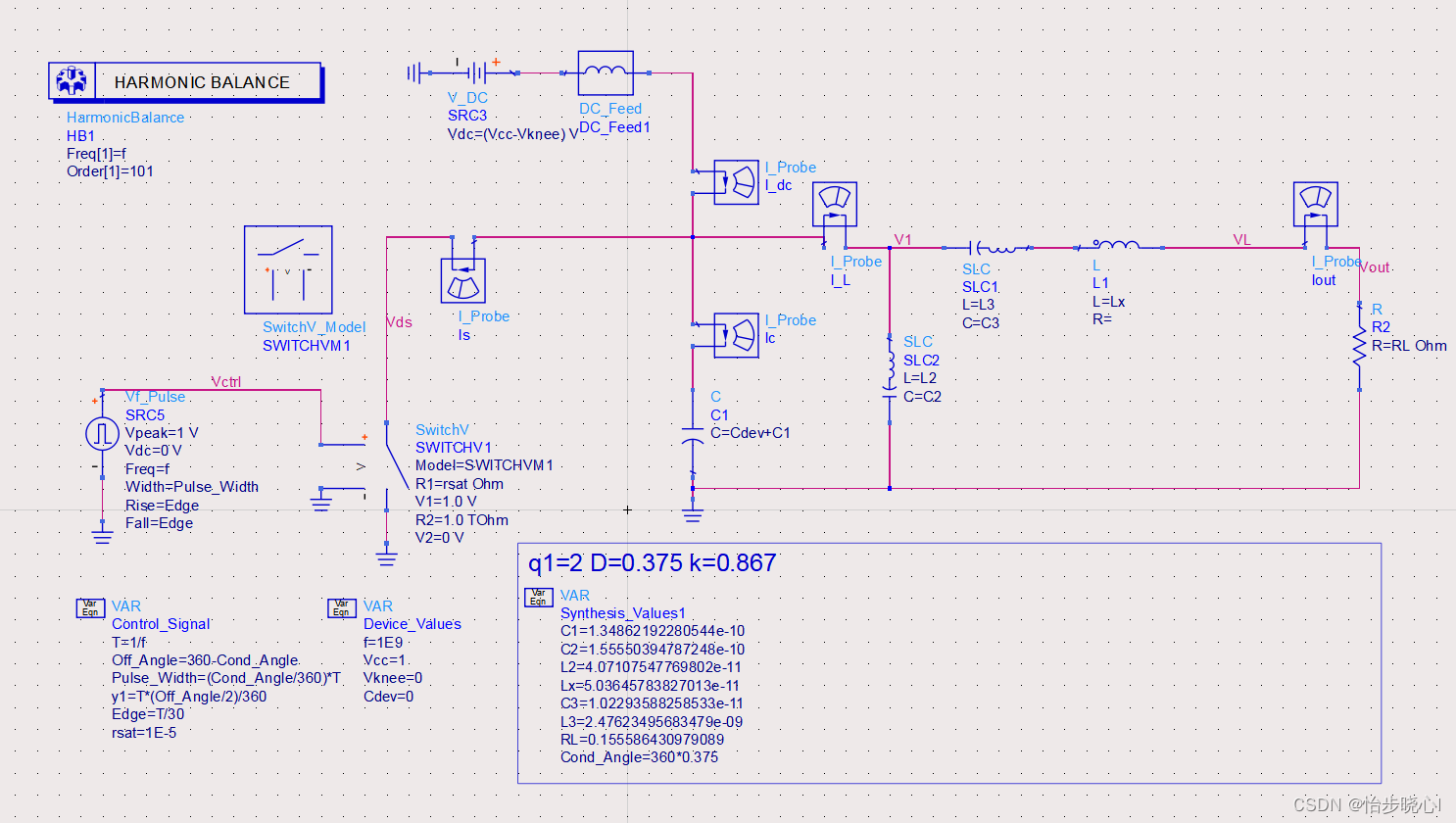
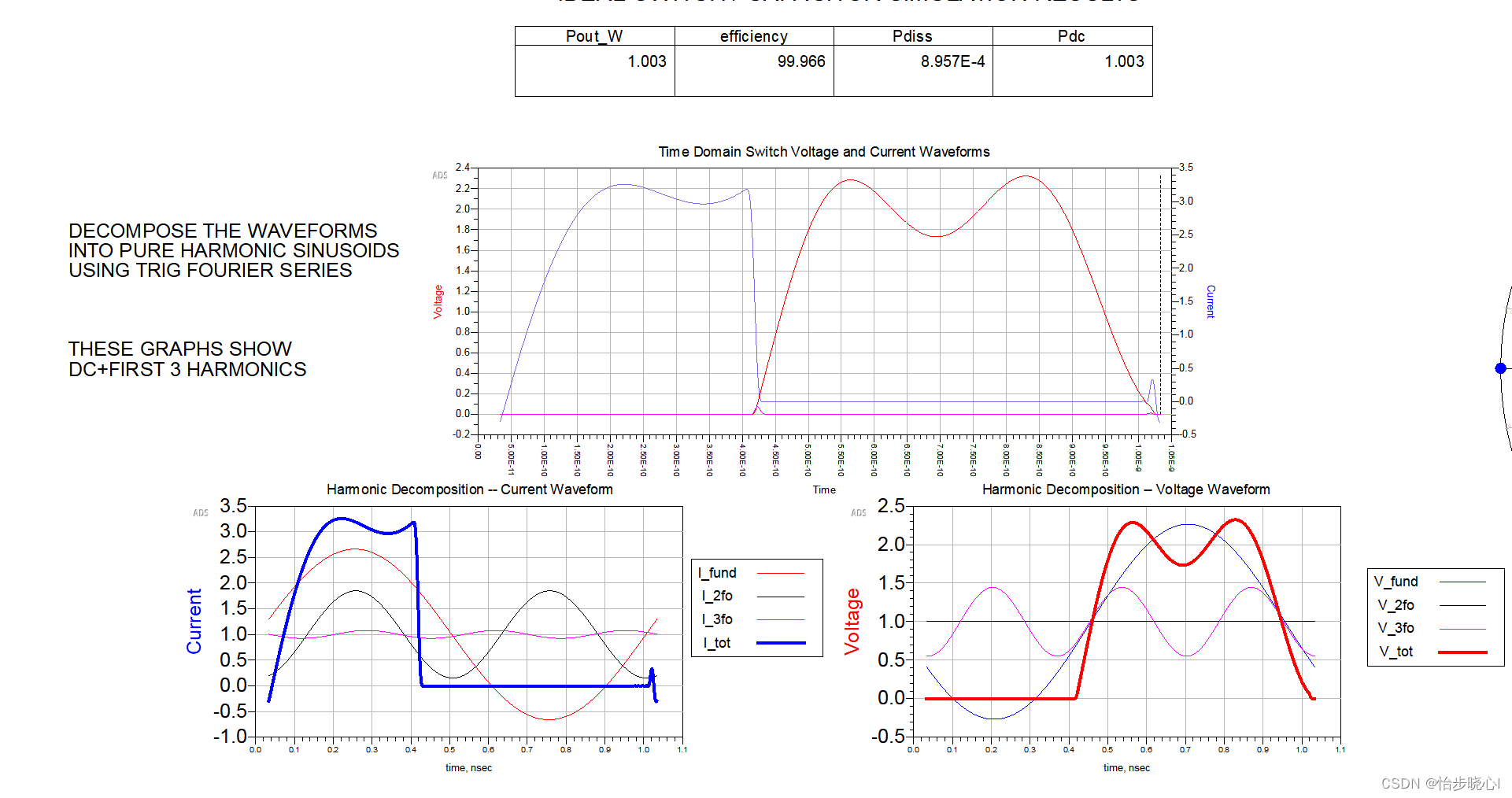
运行仿真,得到的仿真波形如下所示:
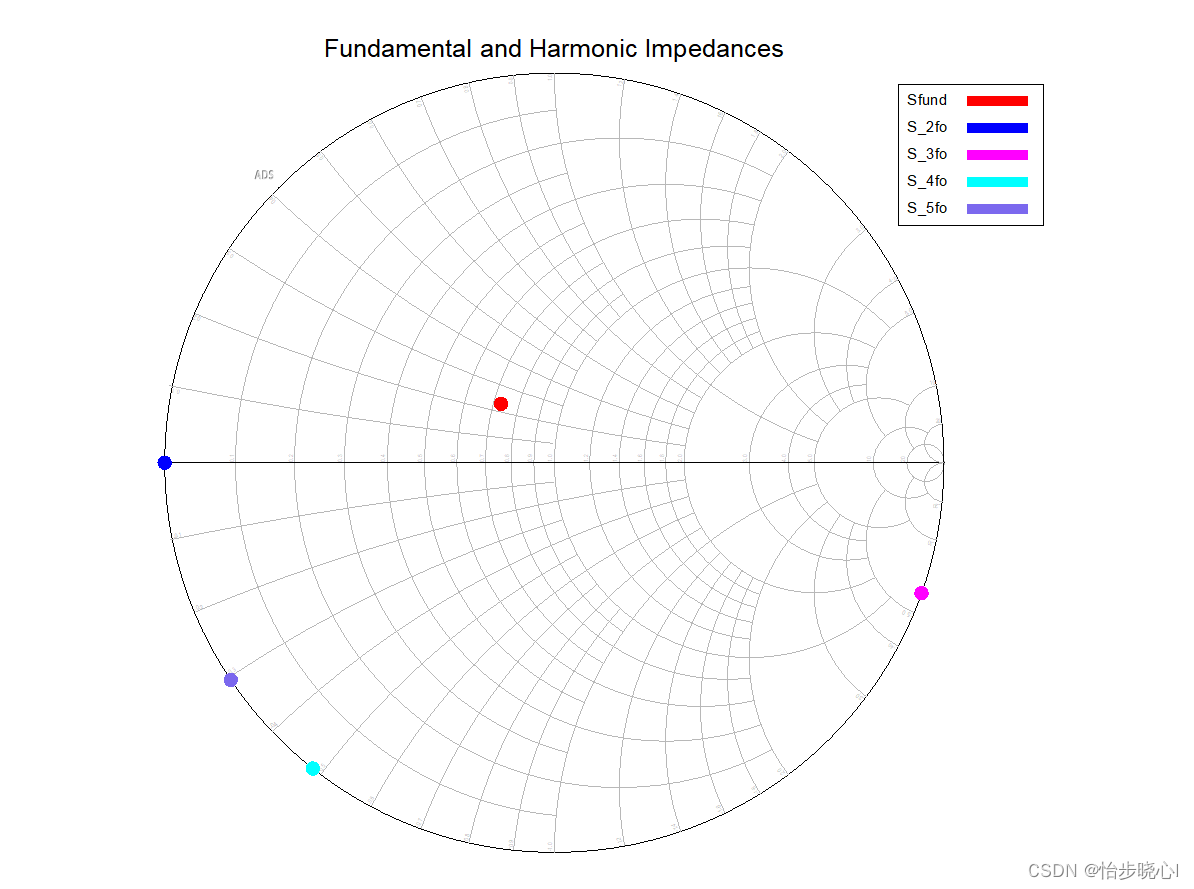
对应的阻抗空间如下所示,其中二次谐波短路正是EF2类的典型特征:
4 、EF类和E/F类的基于MATLAB推导过程
推导的过程主要是解方程,需要满足下面几个ZVDS和ZVS条件:
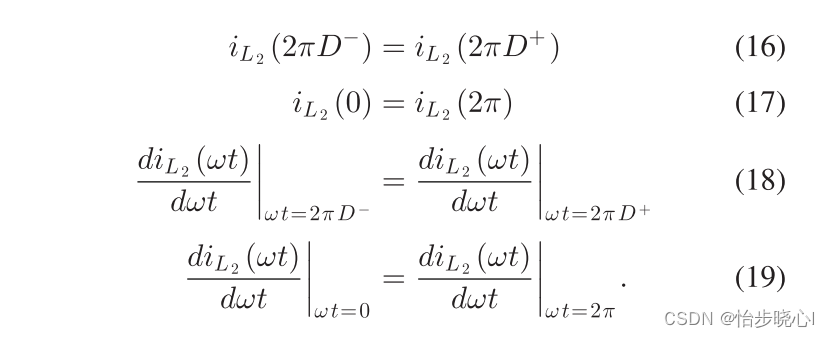
直接解也太麻烦了,所以我们可以使用Matlab的辅助推导来进行求解(classEF_solve.m文件),首先要解出文章中定义变量(A1,B1,A2,B2,p,phi)的表达式,结合上面的条件可以使用solve进行求解,我也是在注释给出了每个等式对应哪个方程:
%% 基本变量计算
clc
clear all
% 已知变量q1 D k,未知变量A1 B1 A2 B2 p phi
syms q1 D k
syms A1 B1 A2 B2 p phi
% Eqn14
q2=(q1*sqrt((k+1)/k));% Eqn5、Eqn12、Eqn16---连续性
eqn1=A1*cos(q1*2*pi*D)+B1*sin(q1*2*pi*D)==A2*cos(q2*2*pi*D)+B2*sin(q2*2*pi*D)-q2^2*p/(q2^2-1)*sin(2*pi*D+phi)+1/(k+1);
% Eqn5、Eqn12、Eqn17---连续性
eqn2=A1==A2*cos(q2*2*pi)+B2*sin(q2*2*pi)-q2^2*p/(q2^2-1)*sin(phi)+1/(k+1);
% Eqn5、Eqn12、Eqn18---导数连续性
eqn3=-A1*q1*sin(q1*2*pi*D)+B1*q1*cos(q1*2*pi*D)==-A2*q2*sin(q2*2*pi*D)+B2*q2*cos(q2*2*pi*D)-q2^2*p/(q2^2-1)*cos(2*pi*D+phi);
% Eqn5、Eqn12、Eqn19---导数连续性
eqn4=B1*q1==-A2*q2*sin(q2*2*pi)+B2*q2*cos(q2*2*pi)-q2^2*p/(q2^2-1)*cos(phi);
% Eqn23
eqn5=2*pi*k*(1-D)/(k+1)+p*(cos(2*pi*D+phi)-cos(phi))*(q2^2/(q2^2-1)-(k+1))+A2/q2*(sin(2*pi*D*q2)-sin(2*pi*q2))+B2/q2*(cos(2*pi*q2)-cos(2*pi*D*q2))==0;
% Eqn24
eqn6=k/(k+1)+p*sin(phi)*(q2^2/(q2^2-1)-(k+1))-(A2*cos(q2*2*pi)+B2*sin(q2*2*pi))==0;[A1,B1,A2,B2,p,phi]=solve(eqn1,eqn2,eqn3,eqn4,eqn5,eqn6,A1,B1,A2,B2,p,phi);simplify(A1)
simplify(B1)
simplify(A2)
simplify(B2)
simplify(p)
simplify(phi)
解出了这些变量就可以继续求目标的波形了,对应的公式也给出了:
%% 波形的计算
clearsyms q1 D k theta
syms A1 B1 A2 B2 p phi
syms tao
% Eqn14
q2=(q1*sqrt((k+1)/k));
assume((D>0)&(D<1))% Eqn12
il2_norm=A2*cos(q2*tao)+B2*sin(q2*tao)-q2^2*p/(q2^2-1)*sin(tao+phi)+1/(k+1);
% Eqn21
ic1_norm=1-p*(k+1)*sin(tao+phi)-il2_norm;
% Eqn26
beta_temp=simplify(int(ic1_norm,tao,2*pi*D,theta));
% Eqn28
vds_norm=simplify(2*pi*beta_temp/(int(beta_temp,theta,2*pi*D,2*pi)));
% Eqn29
is_norm=1-p*(k+1)*sin(theta+phi)-(A1*cos(q1*theta)+B1*sin(q1*theta));
最后是需要计算电路的相关参数,对应的公式也给出在注释,值得注意的是,vx算出来是分段函数,所以最终实现需要用if else语句实现:
%% 电路参数计算
clearsyms q1 D k theta f
syms A1 B1 A2 B2 p phi
syms tao
% Eqn14
q2=(q1*sqrt((k+1)/k));
assume((D>0)&(D<1))
% Eqn12
il2_norm=A2*cos(q2*tao)+B2*sin(q2*tao)-q2^2*p/(q2^2-1)*sin(tao+phi)+1/(k+1);
% Eqn21
ic1_norm=1-p*(k+1)*sin(tao+phi)-il2_norm;
% Eqn26
beta_temp=simplify(int(ic1_norm,tao,2*pi*D,theta));
% Eqn51
beta_integral=int(beta_temp,theta,2*pi*D,2*pi);
% Eqn35
RDC_RL=0.5*((2*pi*(1-D)+A1/q1*sin(2*pi*D*q1)+2*B1/q1*sin(pi*D*q1)^2)/(cos(2*pi*D+phi)-cos(phi)))^2;
% Eqn52
reactance_C1=simplify(2*pi*RDC_RL/beta_integral);
% Eqn58
vx=simplify(2*(int(beta_temp*cos(theta+phi),theta,2*pi*D,2*pi))/(int(beta_temp,theta,2*pi*D,2*pi)));
% Eqn32
im=(2*pi*(1-D)+A1/q1*sin(2*pi*D*q1)+2*B1/q1*sin(pi*D*q1)^2)/(cos(2*pi*D+phi)-cos(phi));
% Eqn51-60
reactance_C2=reactance_C1*k;
reactance_L2=reactance_C2/q1^2;
reactance_Lx=vx/im*RDC_RL;Q_RLC=100;
RL=1/RDC_RL;
C1=1/(2*pi*f*RL*reactance_C1);
C2=1/(2*pi*f*RL*reactance_C2);
L2=reactance_L2*RL/(2*pi*f);
Lx=reactance_Lx*RL/(2*pi*f);
C3=1/(2*pi*f*Q_RLC*RL);
L3=Q_RLC^2*RL^2*C3;





)




)



介绍)

)


