目录
一、基于几何的轨迹跟踪方法
1、基本思想
2、纯追踪
3、Stanly Method
二、PID控制器
三、LQR(Linear Quadratic Regulator)
1、基本思想
2、LQR解法
3、案例学习
基于LQR的路径跟踪
基于LQR的速度跟踪
4、MPC(Model Predicitive Control)
1、基本思想
2、优化思路
3、MPC vs LQR
4、案例学习
系统模型
生成参考状态
数学优化
代价函数设计
约束设计
一、基于几何的轨迹跟踪方法
1、基本思想
基于几何的方法利用车辆和路径之间的几何关系,得到路径跟踪问题的控制律解。基于几何的方法通常利用前视距离来测量车辆前方的误差。该算法的目标是找出每个时刻的前轮角度。
基于几何的轨迹跟踪方法主要有纯跟踪和斯坦福提出的Stanley Method。在几何方法中使用的依然是在前面规划章节使用的自行车模型。
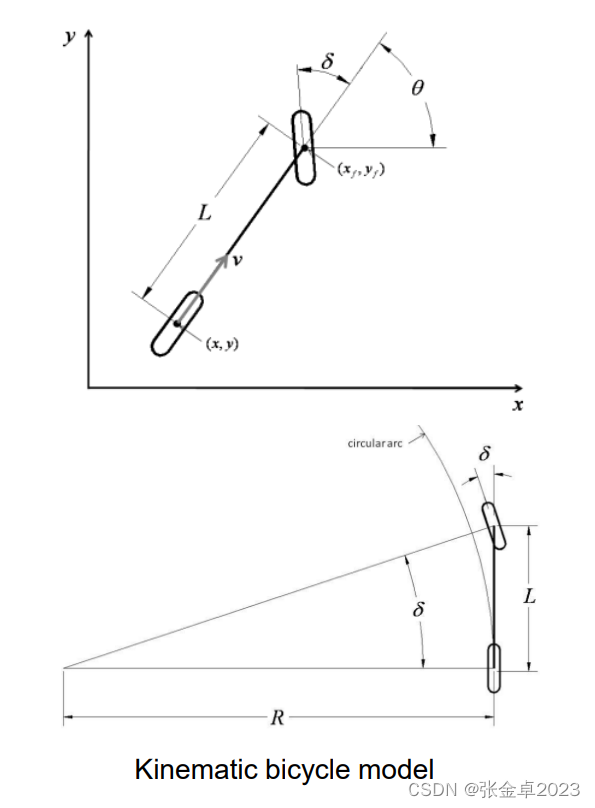
如上图所示,R是在给定转向角度下,后桥沿着的圆周半径。这个模型较好地近似了汽车在低速和中等转向角时的运动。
2、纯追踪

纯追踪方法的最终目的是计算前轮转角,可以通过当前车辆后轴位置到生成目标路径的前视距离la可以得到一条车辆的运动圆弧曲线和路径上的目标点,然后通过几何关系计算得到前轮转角。
角是车身行驶方向与前向距离的夹角,根据数学上的正弦定理,进行如下计算:

使用简单的自行车模型,转向角可以写成:
将曲率代入,可得到纯追踪控制律如下:
为了使得控制律更具有直观性,可以引入一个新的变量cross track error (横跨跟踪误差),该误差描述的是车辆行驶方向与目标点之间的横向距离,那么:
由上式可知,纯追踪方法是一个方向盘角度的比例控制器,它作用在车里前方一些前视距离的横跨追踪误差上,增益为。
在实践中,增益(前视距离)被独立地调整为在几个恒定的速度下保持稳定,从而使更好地被指定为车速的函数。
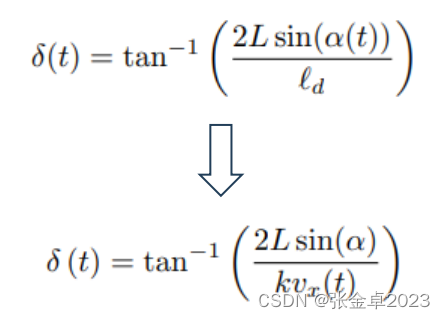
3、Stanly Method
纯追踪方法以车辆后轴为参考点,而Stanly Method以前轴中心为参考点,同时考虑相对于路径最近点的行驶方向和位置误差。
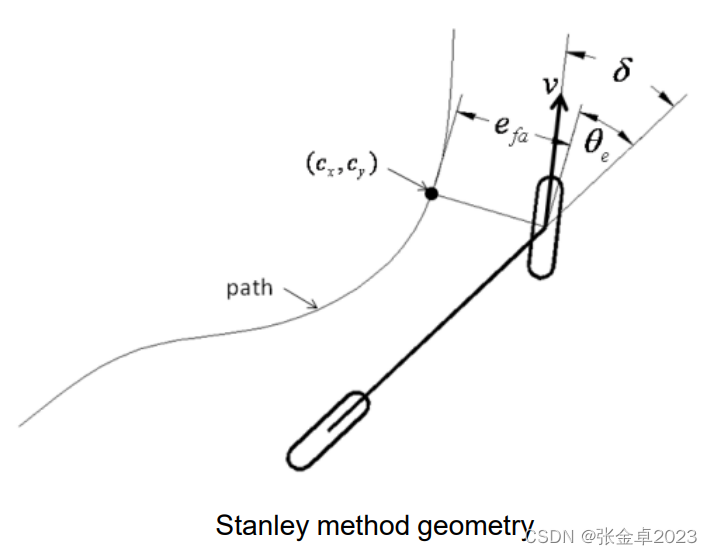
如上图所示,角是前轮偏转角,
是在点
处前轮与路径的夹角,那么前轮要再偏转的角度
为:
Stanly Method使用非线性反馈函数,从前轴中心到最近路径点测量横跨跟踪误差
,公式如下:
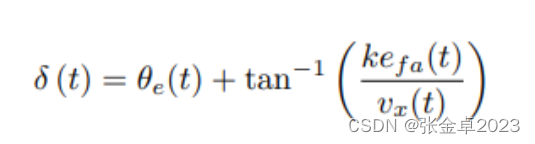
二、PID控制器
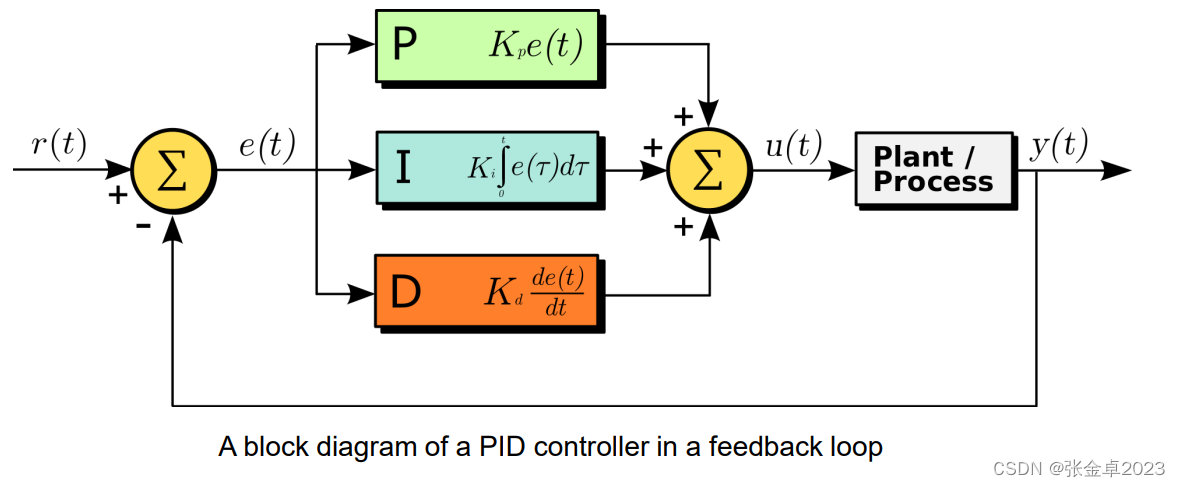
PID控制器试图通过调整控制变量u(t)使误差随时间的误差最小,整体的控制函数如下:
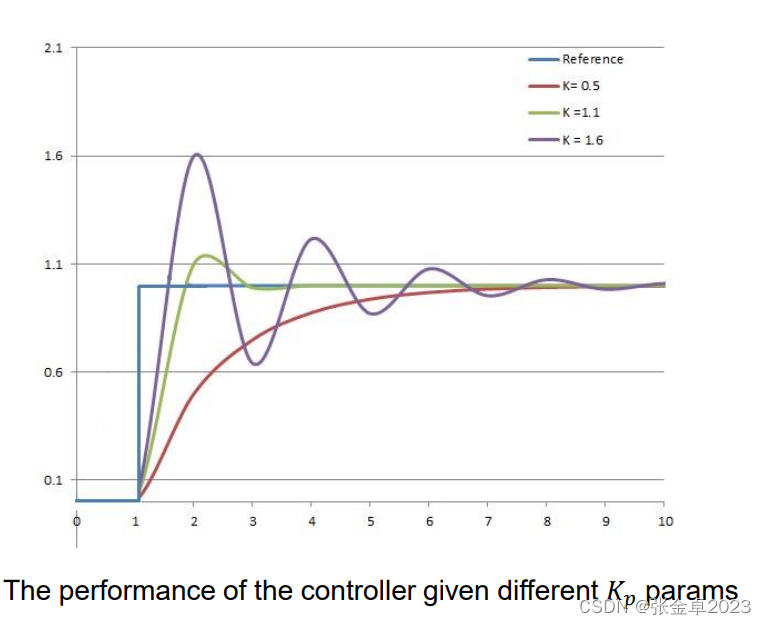
比例项产生一个与当前误差值e(t)成正比的输出值,
被称为比例增益常数。上图可以直观反映比例增益的取值对系统的影响,如果比例增益过高,系统就会变的不稳定,而如果比例增益太低,则当系统发生扰动时,控制作用可能太小。
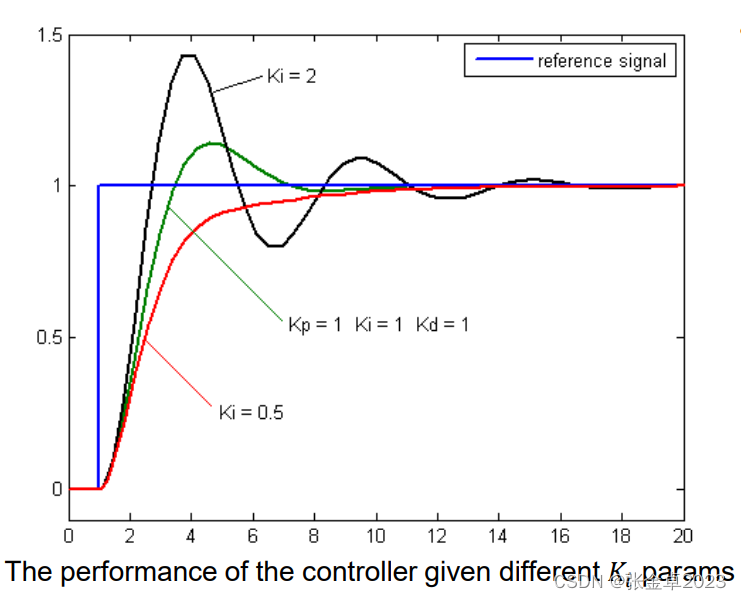
积分项是针对比例控制器工作时存在的稳态误差,稳态误差指的是期望的最终输出与实际输出之间的差值。积分项跟踪累积误差,累计误差乘以积分增益
再添加到控制器输出中。如果积分增益过高,则会导致参考值超调。

为了减小控制的波动性(提高阻尼稳定性),又引入微分项,通过确定误差随时间的斜率来计算微分误差,计算该误差的变化率乘以微分增益
,并加上控制器输出。微分项根据当前变化率来估计误差的未来趋势。误差变化越大,阻尼效应越大,微分项能够提高系统的稳定时间和稳定性。
三、LQR(Linear Quadratic Regulator)
1、基本思想

LQR是一种设计状态变量反馈的方法,它通过最小化一个二次型代价函数来调节线性系统的控制。

每个时间戳的最优控制都可以用下面的公式实现(状态反馈过程):
LQR的整体思路就是给定一个状态量x,通过状态反馈可以得到控制量u,将控制律给到系统作用,得到下一点的状态量然后再重新作为输入量再进行状态反馈,循环迭代直到状态收敛。
状态反馈中K的求解可以通过公式计算得到,其中R和B都是目标函数和线性系统中已知的,而P要通过ARE方程获得:
2、LQR解法
寻找LQR反馈K的设计过程为:
- 选择设计目标函数中的参数矩阵Q和R以及线性系统中的参数矩阵A和B;
- 解关于P的代数方程,由
取得K的值;
- 根据反馈
取得每个状态量对应的控制量。
3、案例学习
基于LQR的路径跟踪
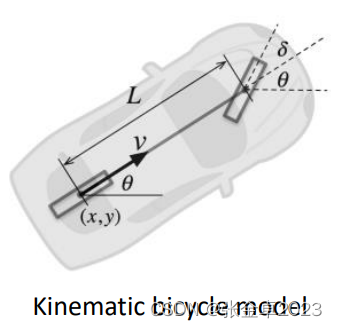
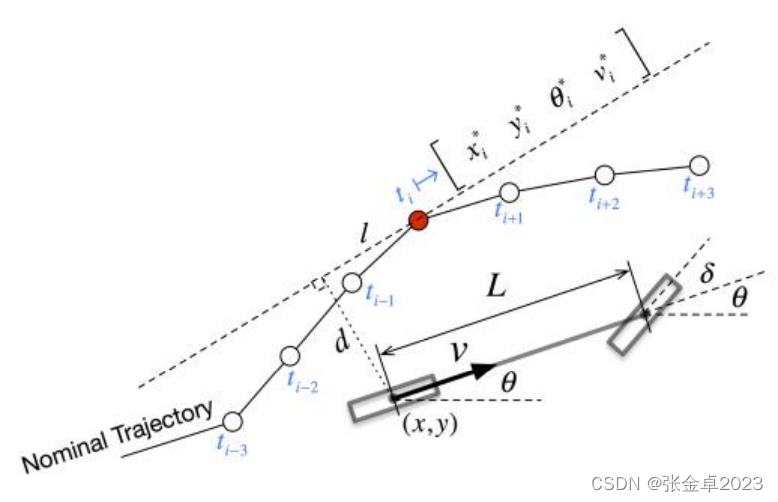
对于传统的自行车模型,可以得到下方的表达式:

:后桥处的参考点姿态(状态量);
:道路上车轮偏转角(状态量);
:纵向速度(状态量);
:转向角变化速率(控制量);
:纵向加速度(控制量);
- L:车轴距离(参数)。
LQR方法要是有标准的线性系统,但自行车模型并不是一个线性系统方程,因此需要对自行车模型做一些转化。
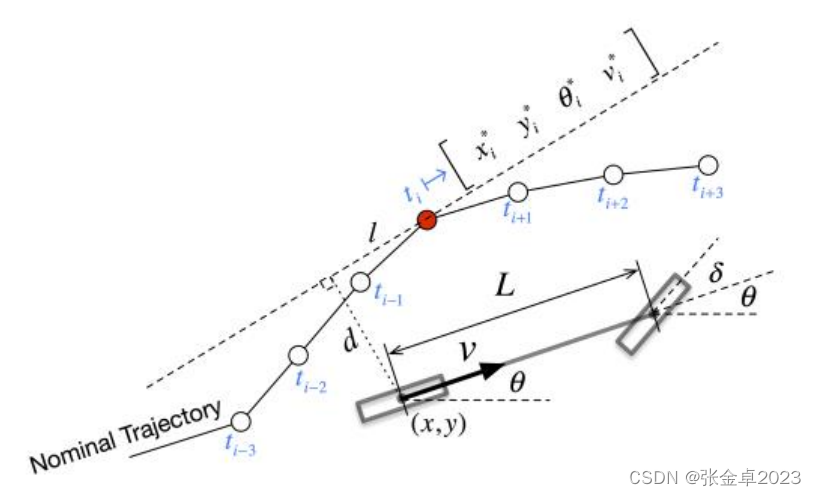
对于横向控制,将状态向量定义为:
横向偏移量为:
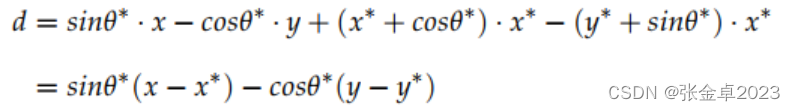
对x的每个维度求导,然后代入自行车模型:

为了获得线性系统方程,需要对上述求导后的结果设置假设:
- 假设一:
要足够小,即车辆航向角与轨迹参考线上的角相差不大;
- 假设二:偏转角
比较小。
那么根据线性系统方程可以写出如下方程:

基于LQR的速度跟踪
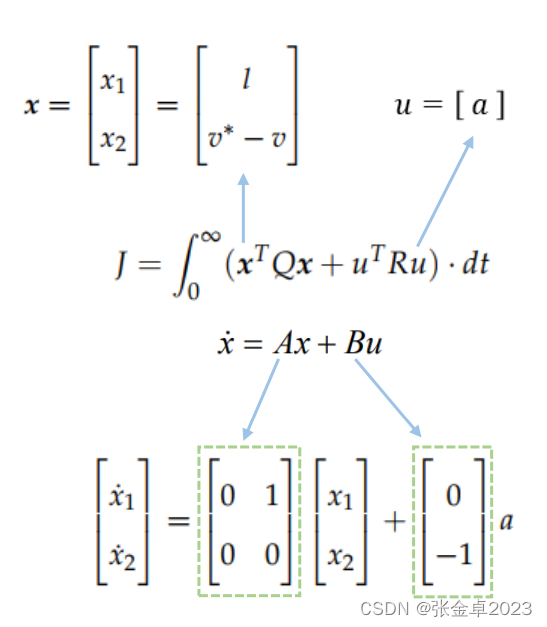
4、MPC(Model Predicitive Control)
1、基本思想
与LQR算法相似,MPC也采用优化的思想进行控制,这种控制技术计算出的控制动作使约束动力系统在有限的、后退的水平的代价函数最小化。
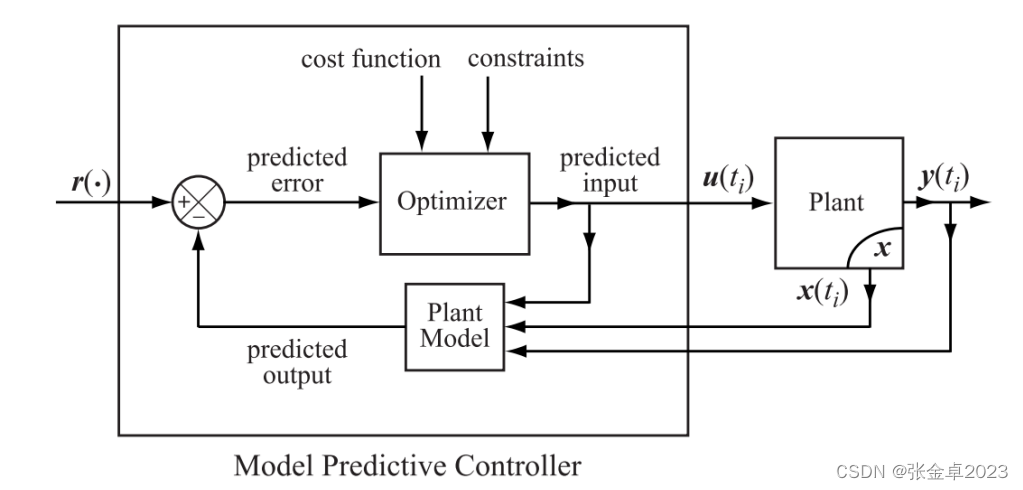
- Model:给定的动力学系统方程;
- Prediction:预测未来的状态;
- 控制:生成最优策略
2、优化思路
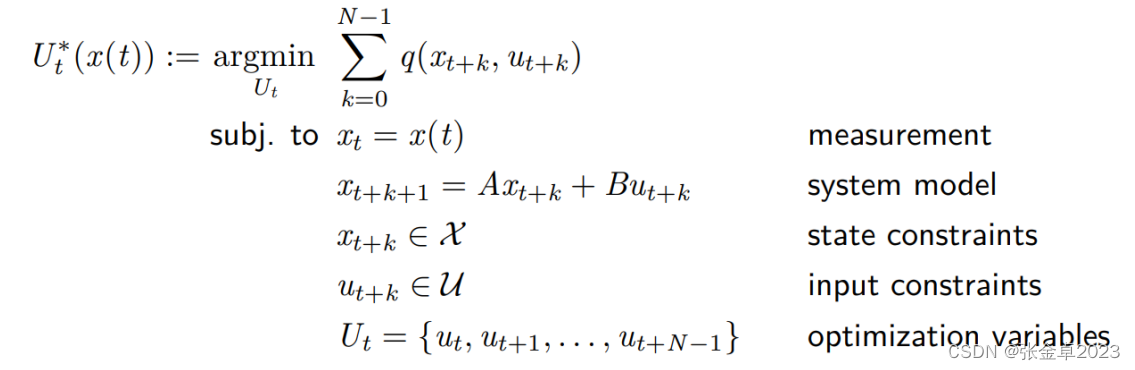
- 最小化的目标有:相对参考线的误差,消耗的能量……
- 预测系统状态的系统模型:可以是线性也可以是非线性;
- 需要满足的约束:控制、状态、线性、非线性……
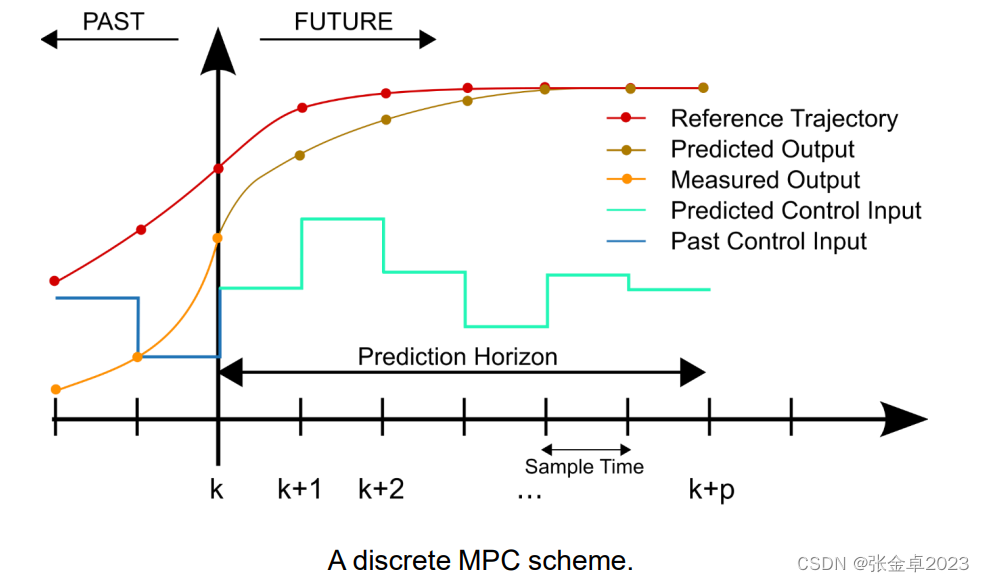
在每一个时间步长(采样间隔),通过求解预测视界的开环优化问题来计算控制量。虽然在预测时域内获取了很多时间戳上的最优控制策略,但是在当前时间点只应用计算控制序列的第一个值。然后在下一个时间步长,得到新的系统状态并重新计算。
虽然我们在当前时间点只应用第一个时间戳的优化策略,但是仍然要计算一个较大预测时域内的控制策略,是采用了类似前面基于几何方法控制中的“前视距离”的思想,能够让系统考虑得更远,以更加平缓的方式接近参考线,即未雨绸缪,决策当下。
3、MPC vs LQR

- MPC和LQR都是最优控制的表达式,但它们的优化代价设置方案不同;
- LQR优化整个预测时域内,而MPC则更像是优化一个滑动窗口,每次都优化后一个时间窗口;
- LQR具有较好的全局稳定性,因为它考虑的是整个时间域内的轨迹,而MPC通常具有较好的局部最优性;
- MPC对线性没有任何假设,它可以处理线性或非线性约束,状态转移方程也可以是非线性的,而这都是LQR的缺点。
4、案例学习
系统模型
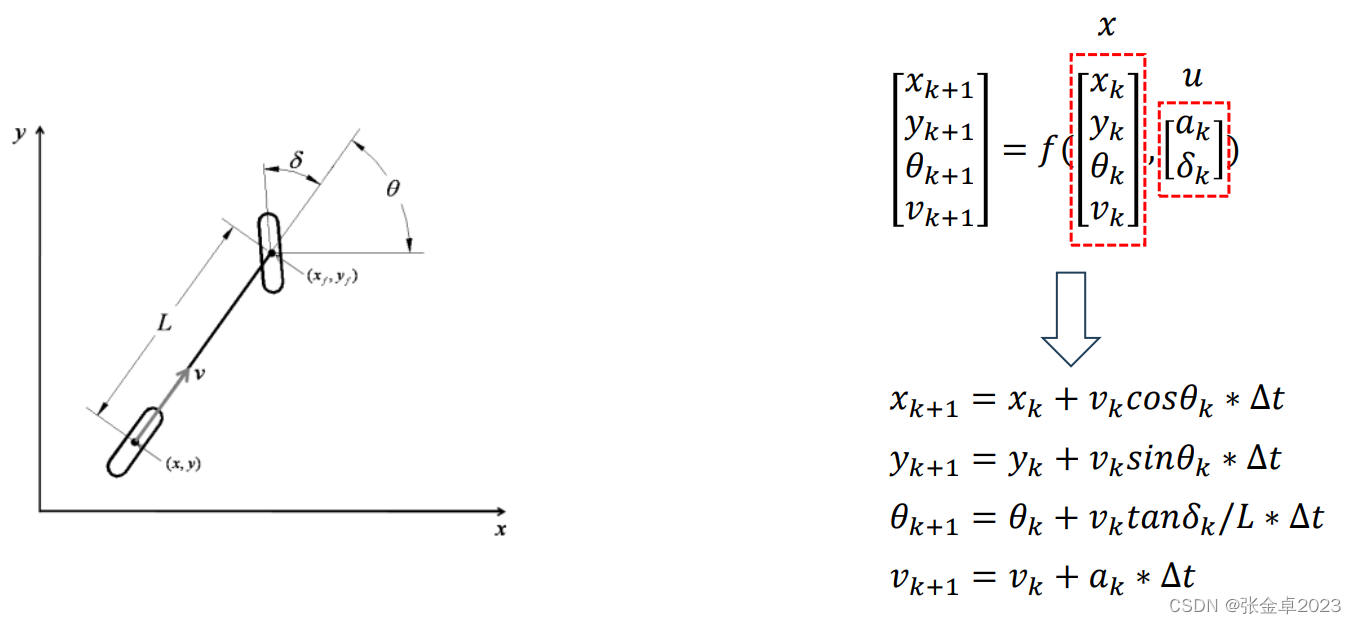
为了简化问题,这里我们直接使用自行车模型,和前面类似,不再叙述。
生成参考状态
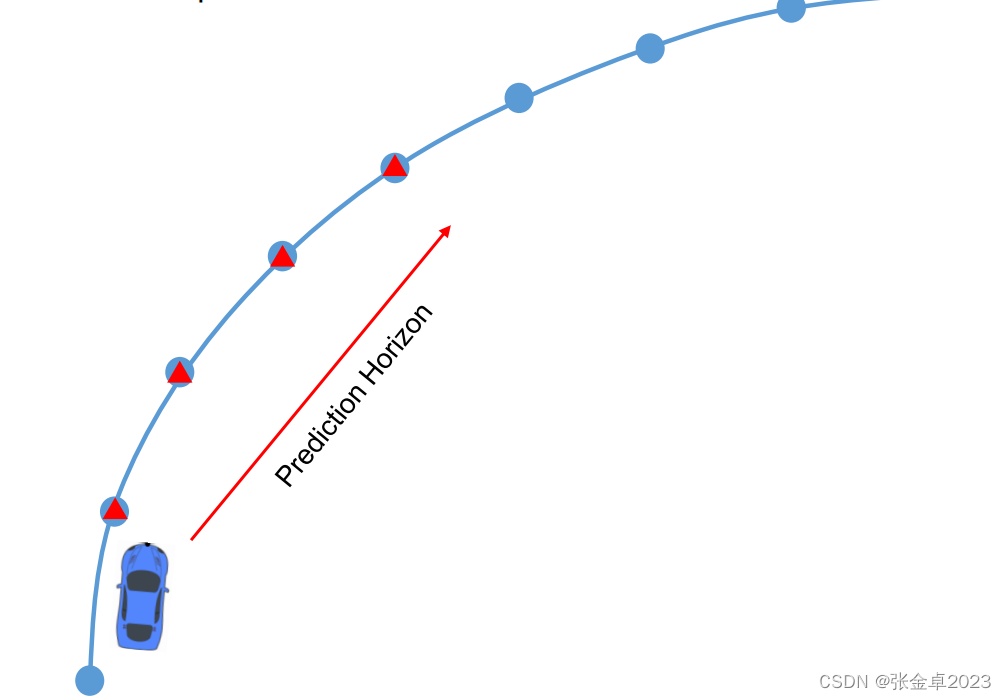
给定规划的轨迹和车辆的当前状态,生成参考状态预测范围内的状态。相比较规划模块较长的预测时域,控制模块对实时性的要求更高,频率更高,相对的预测时域就要小很多。
数学优化
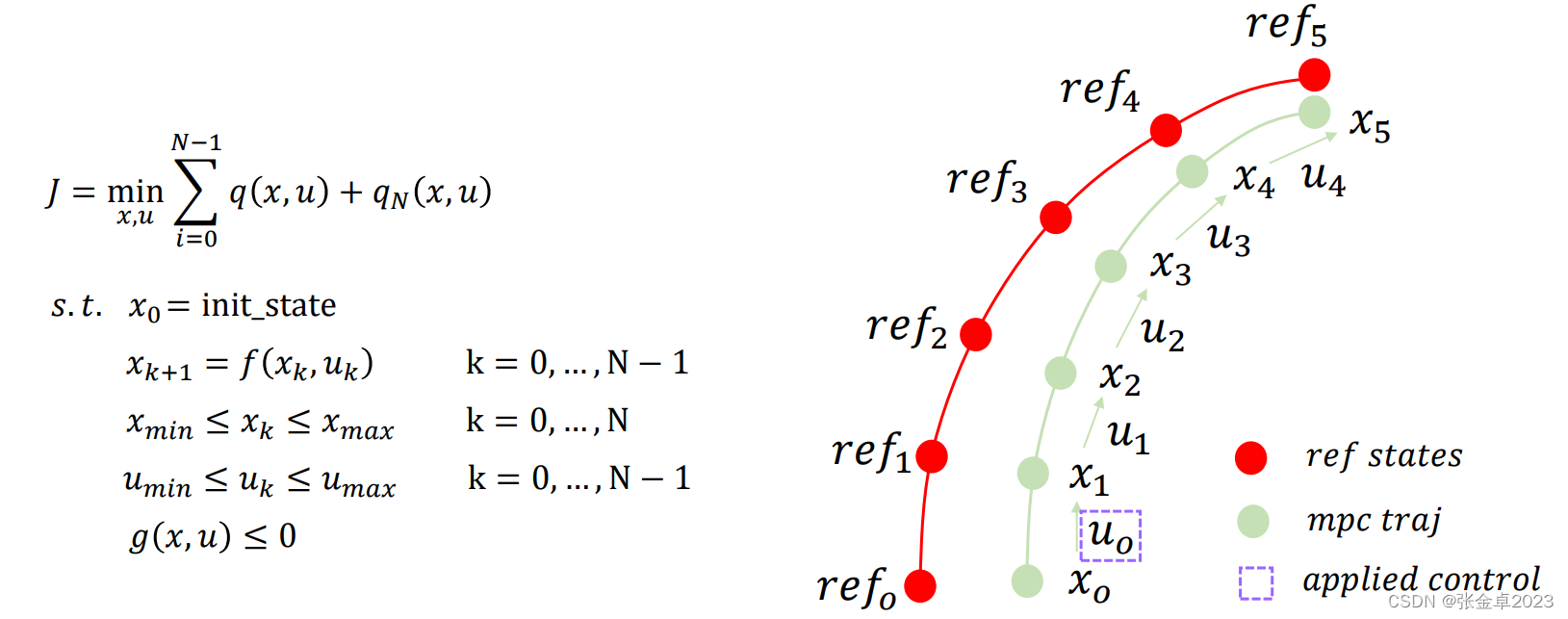 在优化模块设置目标函数和设置各种约束条件。
在优化模块设置目标函数和设置各种约束条件。
代价函数设计
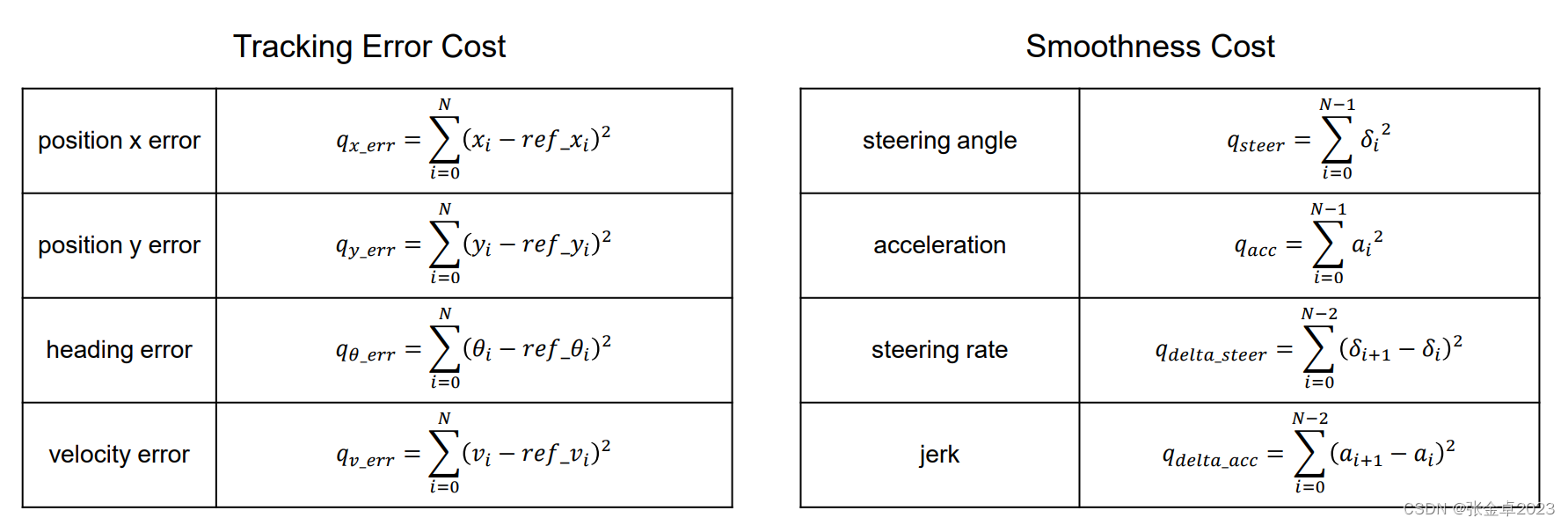
一般来讲,代价函数由两部分组成,一部分是跟踪轨迹的误差代价(对应左上Tracking Error Cost),另一部分是车辆运动时考虑平顺性的代价(对应右上Smoothness Cost)。
约束设计
自行车模型和动态约束:

初始约束:

状态/控制边界约束:
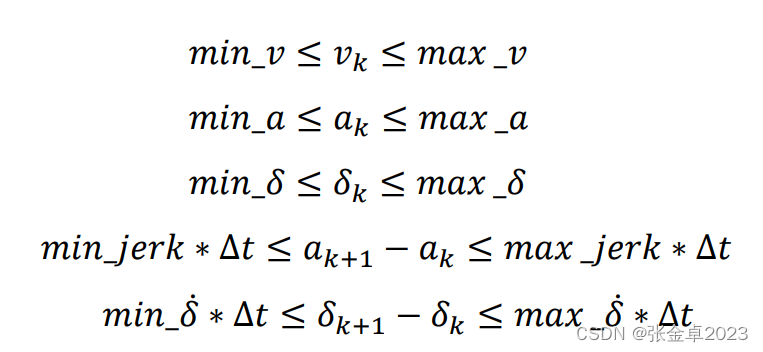


![【洛谷 P8668】[蓝桥杯 2018 省 B] 螺旋折线 题解(数学+平面几何)](http://pic.xiahunao.cn/【洛谷 P8668】[蓝桥杯 2018 省 B] 螺旋折线 题解(数学+平面几何))

ALGO-981 过河马)
、get_Columns()及get_Count()函数的用法及区别是什么?)


)


![[数据集][目标检测]遥感图像游泳池检测数据集VOC+YOLO格式288张1类别](http://pic.xiahunao.cn/[数据集][目标检测]遥感图像游泳池检测数据集VOC+YOLO格式288张1类别)



![[N1CTF 2018]eating_cms 不会编程的崽](http://pic.xiahunao.cn/[N1CTF 2018]eating_cms 不会编程的崽)



:消息队列MQ)