在深度学习中，对时间序列的处理主要涉及到以下几个方面：

1. 序列建模：深度学习可以用于对时间序列进行建模。常用的模型包括循环神经网络（Recurrent Neural Networks, RNN）和长短期记忆网络（Long Short-Term Memory, LSTM）。这些模型可以在输入序列的基础上进行学习，捕捉序列中的时间关系和时序模式。

2. 序列预测：深度学习也可以用于时间序列的预测。通过对历史数据进行建模，可以利用深度学习模型来预测未来的数值或趋势。常用的模型包括循环神经网络（RNN）和卷积神经网络（Convolutional Neural Networks, CNN）。

3. 应用领域：深度学习在时间序列的处理中被广泛应用于各个领域。例如，金融领域中可以利用深度学习模型来预测股票价格；气象领域中可以利用深度学习模型来预测天气变化；语音识别领域中可以利用深度学习模型来识别语音信号中的文字内容。

总的来说，深度学习在时间序列的处理中能够利用神经网络的强大表达能力，通过学习历史数据的模式和规律，来进行序列的建模和预测。这使得深度学习成为处理时间序列数据的一种强大工具。

政安晨的个人主页：政安晨

欢迎 👍点赞✍评论⭐收藏

收录专栏: 政安晨的机器学习笔记

希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正！

不同类型的时间序列任务

时间序列（timeseries）是指定期测量获得的任意数据，比如每日股价、城市每小时耗电量或商店每周销售额。

无论是自然现象（如地震活动、鱼类种群的演变或某地天气）还是人类活动模式（如网站访问者、国家GDP或信用卡交易），时间序列都无处不在。

与前面遇到的数据类型不同，处理时间序列需要了解系统的动力学（dynamics），包括系统的周期性循环、系统随时间如何变化、系统的周期规律与突然激增等。

目前，最常见的时间序列任务是预测：预测序列接下来会发生什么。

比如提前几小时预测用电量，以便于预计需求；

提前几个月预测收入，以便于制订预算计划；

提前几天预测天气，以便于规划日程。预测是本章的重点内容。

但实际上，你还可以对时间序列做很多其他事情。

分类：为时间序列分配一个或多个分类标签。例如，已知一名网站访问者的活动时间序列，判断该访问者是机器人还是人类。

事件检测：识别连续数据流中特定预期事件的发生。一个特别有用的应用是“热词检测”，模型监控音频流并检测像“Ok Google”或“Hey Alexa”这样的话。

异常检测：检测连续数据流中出现的异常情况。

公司网络出现异常活动？可能是有攻击者。

生产线出现异常读数？是时候让人去查看一下了。

异常检测通常是通过无监督学习实现的，因为你通常不知道要检测哪种异常，所以无法针对特定的异常示例进行训练。

处理时间序列时，你会遇到许多特定领域的数据表示方法。例如，你可能听说过傅里叶变换，它是指将一系列值表示为不同频率的波的叠加。对那些以周期和振荡为主要特征的数据（如声音、摩天大楼的振动或人的脑电波）进行预处理时，傅里叶变换可以发挥很大作用。对于深度学习而言，傅里叶分析（或相关的梅尔频率分析）与其他特定领域的表示可以用来做特征工程。这是一种在训练模型之前准备数据的方式，以便让模型更容易运行。然而，这篇文章不会介绍这些技术，而是将重点放在构建模型上。

咱们这篇文章将介绍循环神经网络（recurrent neural network，RNN）及如何将其应用于时间序列预测。

温度预测示例

咱们这篇文章所有代码示例都针对同一个问题：已知每小时测量的气压、湿度等数据的时间序列（数据由屋顶的一组传感器记录），预测24小时之后的温度。你会发现，这是一个相当有挑战性的问题。

利用这个温度预测任务，我们会展示时间序列数据与之前见过的各类数据集在本质上有哪些不同。你会发现，密集连接网络和卷积神经网络并不适合处理这种数据集，而另一种机器学习技术——循环神经网络——在这类问题上大放异彩。

我们将使用一个天气时间序列数据集，它由德国耶拿的马克斯•普朗克生物地球化学研究所的气象站记录。在这个数据集中，每10分钟记录14个物理量（如温度、气压、湿度、风向等），其中包含多年的记录。原始数据可追溯至2003年，但本例仅使用2009年～2016年的数据。

咱们在Jupyter中下载这个数据集并解压：

!wget https://s3.amazonaws.com/keras-datasets/jena_climate_2009_2016.csv.zip
!unzip jena_climate_2009_2016.csv.zip

解压数据：

接下来咱们查看数据：

（查看耶拿天气数据集）

import os
fname = os.path.join("jena_climate_2009_2016.csv")with open(fname) as f:data = f.read()lines = data.split("\n")
header = lines[0].split(",")
lines = lines[1:]
print(header)
print(len(lines))

演绎执行如下：

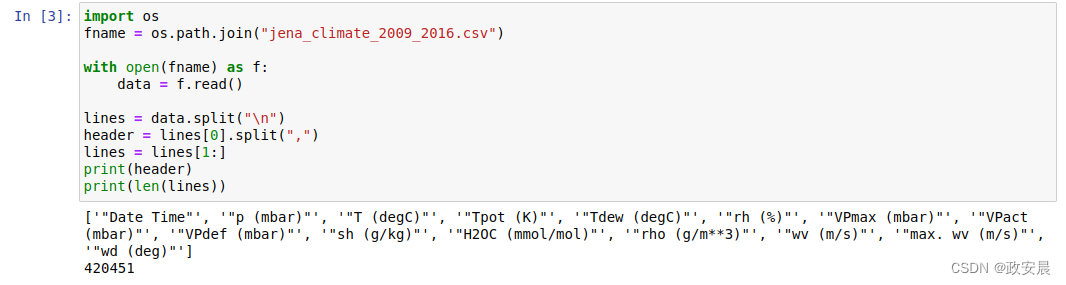
从输出可以看出，共有420 451行数据（每行数据是一个时间步，记录了1个日期和14个与天气有关的值），输出还包含以上表头。

接下来，我们将所有420 451行数据转换为NumPy数组，代码如下所示：一个数组包含温度（单位为摄氏度），另一个数组包含其他数据。我们将使用这些特征来预测温度。请注意，我们舍弃了"Date Time"（日期和时间）这一列。

（解析数据）

import numpy as np
temperature = np.zeros((len(lines),))
raw_data = np.zeros((len(lines), len(header) - 1))
for i, line in enumerate(lines):values = [float(x) for x in line.split(",")[1:]]# 将第1列保存在temperature数组中temperature[i] = values[1]# 将所有列（包括温度）保存在raw_data数组中raw_data[i, :] = values[:]

我们来绘制温度随时间的变化曲线（单位为摄氏度），代码如下所示。在这张图中，你可以清楚地看到温度的年度周期性变化，数据跨度为8年。

（绘制温度时间序列）

from matplotlib import pyplot as plt
plt.plot(range(len(temperature)), temperature)

如果您的环境中还没有matplotlib，可以参考我的这篇文章安装：

政安晨：在Jupyter中【示例演绎】Matplotlib的官方指南（一）{Pyplot tutorial}https://blog.csdn.net/snowdenkeke/article/details/136096870执行如下：

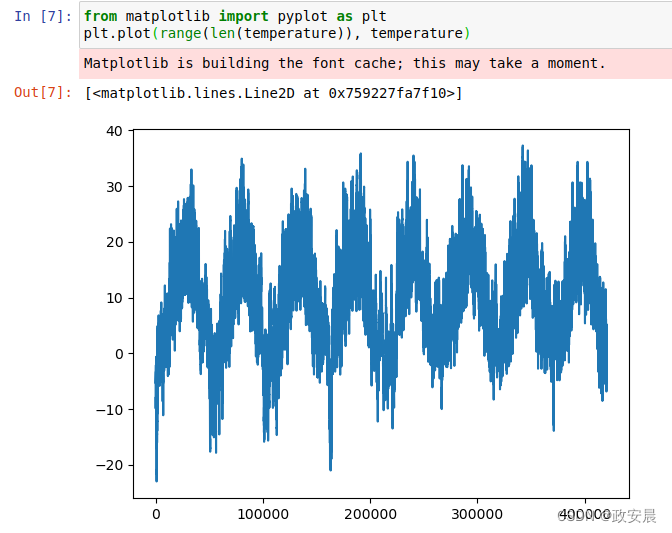
上面这个是数据集整个时间范围内的温度（℃）。

现在，我们来绘制前10天温度数据的曲线，代码如下所示。由于每10分钟记录一次数据，因此每天有144个数据点（24×6=144）。

（绘制前10天的温度时间序列）

plt.plot(range(1440), temperature[:1440])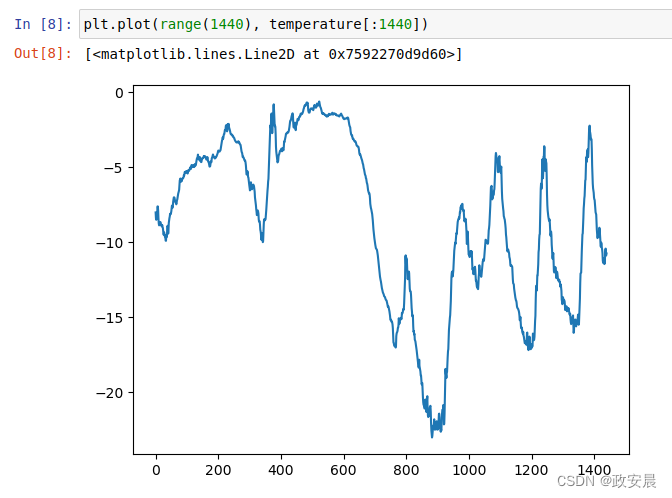

从上图中可以看到每天的周期性变化，尤其是最后4天特别明显。另外请注意，这10天一定是来自于寒冷的冬季月份。

始终在数据中寻找周期性

在多个时间尺度上的周期性，是时间序列数据非常重要且常见的属性。

无论是天气、商场停车位使用率、网站流量、杂货店销售额，还是健身追踪器记录的步数，你都会看到每日周期性和年度周期性（人类生成的数据通常还有每周的周期性）。

探索数据时，一定要注意寻找这些模式。

对于这个数据集，如果你想根据前几个月的数据来预测下个月的平均温度，那么问题很简单，因为数据具有可靠的年度周期性。但如果查看几天的数据，那么你会发现温度看起来要混乱得多。以天作为观察尺度，这个时间序列是可预测的吗？我们来寻找这个问题的答案。

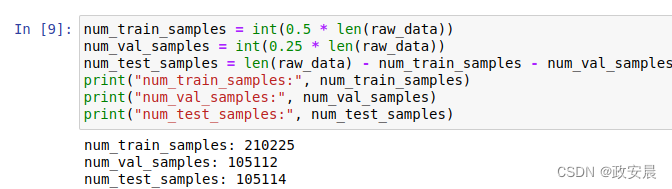
在后续所有实验中，我们将前50%的数据用于训练，随后的25%用于验证，最后的25%用于测试，代码如下所示。处理时间序列数据时，有一点很重要：验证数据和测试数据应该比训练数据更靠后，因为你是要根据过去预测未来，而不是反过来，所以验证/测试划分应该反映这一点。如果将时间轴反转，有些问题就会变得简单得多。

（这段代码是计算用于训练、验证和测试的样本数）

num_train_samples = int(0.5 * len(raw_data))
num_val_samples = int(0.25 * len(raw_data))
num_test_samples = len(raw_data) - num_train_samples - num_val_samples
print("num_train_samples:", num_train_samples)
print("num_val_samples:", num_val_samples)
print("num_test_samples:", num_test_samples)

执行如下：

准备数据

这个问题的确切表述如下：每小时采样一次数据，给定前5天的数据，我们能否预测24小时之后的温度？

我们对数据进行预处理，将其转换为神经网络可以处理的格式。这很简单。因为数据已经是数值型的，所以不需要做向量化。但数据中的每个时间序列位于不同的范围，比如气压大约在1000毫巴（mbar）1，而水汽浓度（H2OC）大约为3毫摩尔/摩尔（mmol/mol）。我们将对每个时间序列分别做规范化，使其处于相近的范围，并且都取较小的值，代码如下所示：我们使用前210 225个时间步作为训练数据，所以只计算这部分数据的均值和标准差。

（如下代码为数据规范化）

mean = raw_data[:num_train_samples].mean(axis=0)
raw_data -= mean
std = raw_data[:num_train_samples].std(axis=0)
raw_data /= std

接下来我们创建一个Dataset对象，它可以生成过去5天的数据批量，以及24小时之后的目标温度。由于数据集中的样本是高度冗余的（对于样本N和样本N+1，二者的大部分时间步是相同的），因此显式地保存每个样本将浪费资源。相反，我们将实时生成样本，仅保存最初的数组raw_data和temperature。

我们可以轻松地编写一个Python生成器来完成这项工作，但也可以直接利用Keras内置的数据集函数（timeseries_dataset_from_array()），从而减少工作量。一般来说，你可以将这个函数用于任意类型的时间序列预测任务。

理解timeseries_dataset_from_array()

为了理解timeseries_dataset_from_array()的作用，我们来看一个简单的例子。这个例子的大致思想是：给定一个由时间序列数据组成的数组（data参数），timeseries_dataset_from_array()可以给出从原始时间序列中提取的窗口（我们称之为“序列”）。

举个例子，对于data = [0, 1, 2, 3, 4, 5, 6]和sequence_length = 3，timeseries_dataset_from_array()将生成以下样本：[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4,5], [4, 5, 6]。

你还可以向timeseries_dataset_from_array()传入targets参数（一个数组）。targets数组的第一个元素应该对应data数组生成的第一个序列的预期目标。因此，做时间序列预测时，targets应该是与data大致相同的数组，并偏移一段时间。

例如，对于data = [0, 1, 2, 3, 4, 5, 6, ...]和sequence_length = 3，你可以传入targets = [3,4, 5, 6, ...]，创建一个数据集并预测时间序列的下一份数据。我们来试一下。

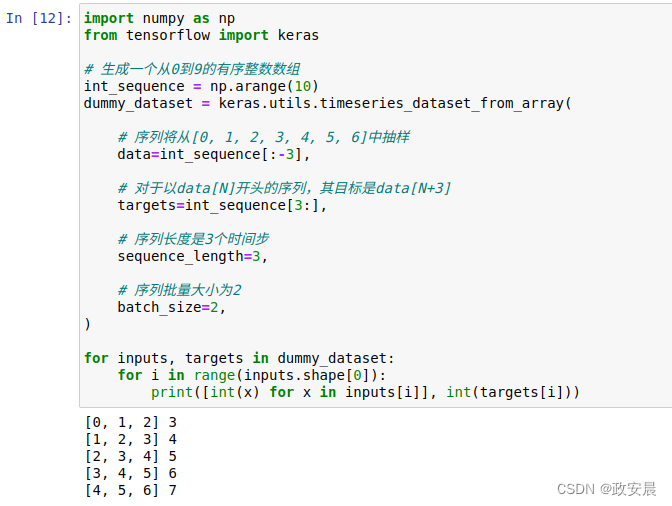
import numpy as np
from tensorflow import keras# 生成一个从0到9的有序整数数组
int_sequence = np.arange(10)
dummy_dataset = keras.utils.timeseries_dataset_from_array(# 序列将从[0, 1, 2, 3, 4, 5, 6]中抽样data=int_sequence[:-3],# 对于以data[N]开头的序列，其目标是data[N+3]targets=int_sequence[3:],# 序列长度是3个时间步sequence_length=3,# 序列批量大小为2batch_size=2,
)for inputs, targets in dummy_dataset:for i in range(inputs.shape[0]):print([int(x) for x in inputs[i]], int(targets[i]))

代码运行如下：

我们将使用timeseries_dataset_from_array()来创建3个数据集，分别用于训练、验证和测试，代码如下所示：

我们将使用以下参数值。

sampling_rate = 6：观测数据的采样频率是每小时一个数据点，也就是说，每6个数据点保留一个。

sequence_length = 120：给定过去5天（120小时）的观测数据。

delay = sampling_rate * (sequence_length + 24- 1)：序列的目标是序列结束24小时之后的温度。创建训练数据集时，我们传入start_index = 0和end_index = num_train_samples，只使用前50%的数据。对于验证数据集，我们传入start_index =num_train_samples和end_index =num_train_samples + num_val_samples，使用接下来25%的数据。最后对于测试数据集，我们传入start_index =num_train_samples + num_val_samples，使用剩余数据。

创建3个数据集，分别用于训练、验证和测试：

sampling_rate = 6
sequence_length = 120
delay = sampling_rate * (sequence_length + 24 - 1)
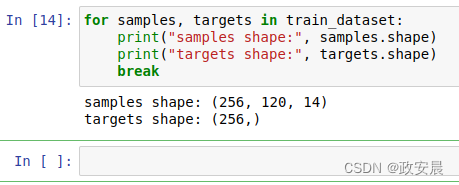
batch_size = 256train_dataset = keras.utils.timeseries_dataset_from_array(raw_data[:-delay],targets=temperature[delay:],sampling_rate=sampling_rate,sequence_length=sequence_length,shuffle=True,batch_size=batch_size,start_index=0,end_index=num_train_samples)val_dataset = keras.utils.timeseries_dataset_from_array(raw_data[:-delay],targets=temperature[delay:],sampling_rate=sampling_rate,sequence_length=sequence_length,shuffle=True,batch_size=batch_size,start_index=num_train_samples,end_index=num_train_samples + num_val_samples)test_dataset = keras.utils.timeseries_dataset_from_array(raw_data[:-delay],targets=temperature[delay:],sampling_rate=sampling_rate,sequence_length=sequence_length,shuffle=True,batch_size=batch_size,start_index=num_train_samples + num_val_samples)

每个数据集都会生成一个元组(samples, targets)，其中samples是包含256个样本的批量，每个样本包含连续120小时的输入数据；targets是包含相应的256个目标温度的数组。请注意，因为样本已被随机打乱，所以一批数据中的两个连续序列（如samples[0]和samples[1]）不一定在时间上接近。我们来查看数据集的输出，如下代码所示：

（查看一个数据集的输出）

for samples, targets in train_dataset:print("samples shape:", samples.shape)print("targets shape:", targets.shape)break

演绎如下：

---

咱们先告一段落，下篇文章继续。