基于禁忌搜索算法（TS）的TSP（Python实现）

本篇文章是博主在最化优学习、人工智能等领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对相关等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在最优化算法：

最优化算法（1）---《基于禁忌搜索算法（TS）的TSP（Python实现）》

基于禁忌搜索算法（TS）的TSP（Python实现）

1.项目介绍

2.程序代码

3.运行结果

1.项目介绍

基于禁忌搜索算法（TS）的TSP（Traveling Salesman Problem，旅行商问题），涉及一种用于解决TSP的优化方法。TSP是一个经典的组合优化问题，目标是寻找一条最短路径，使得旅行商可以访问每个城市恰好一次并返回起点城市。

TS算法作为一种启发式优化算法，在TSP求解中具有广泛的应用。相较于传统的穷举或贪婪算法，TS算法通过引入禁忌列表和邻域结构来更全面地探索解空间，从而更有可能找到较为优秀的近似最优解。

禁忌搜索算法从一个初始解开始，在每次迭代中根据邻域结构生成新的解，并根据目标函数对其质量进行评估。若新解优于当前最优解且未出现在禁忌列表中，则接受该解作为当前最优解；否则，寻找下一个最佳候选解。同时，禁忌列表会记录一段时间内禁止选择的解，以避免陷入循环或重复访问相似解的情况。

在TSP问题上，邻域结构通常包括交换两个城市的位置、翻转子路径等操作，而目标函数则是路径长度。禁忌搜索通过不断迭代搜索和更新禁忌列表，逐步改进当前路径，直至满足结束条件为止。

在基于TS算法求解TSP问题时，禁忌搜索的核心思想包括以下几个方面：

禁忌列表：记录已经探索过的路径或解，以避免下一步重复探索相同的路径或解。
邻域结构：定义了TSP解空间中可行解之间的相邻关系，如通过交换、插入等操作生成新的解。
目标函数：通常是TSP问题中路径长度的计算，用于评估每个解的质量。

TS算法求解TSP的基本步骤包括：

初始化：随机生成初始路径
迭代搜索：根据邻域结构和目标函数，通过禁忌搜索不断调整路径，并更新禁忌列表，记录当前最优路径
终止条件：达到预设的迭代次数或满足特定条件时结束搜索，返回最优路径

通过利用TS算法求解TSP问题，可以有效地寻找到较为优秀的旅行路线，虽不能保证找到全局最优解，但通常能获得接近最优解的结果。

2.程序代码

""""
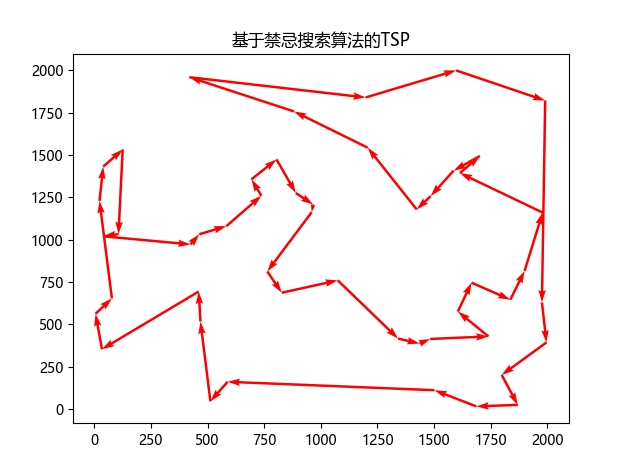
题目：基于禁忌搜索算法的TSP
作者：Rainbook
最终修改时间：2023.12.30
"""
import math
import random
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
import numpy as npplt.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 使用微软雅黑字体
plt.rcParams['axes.unicode_minus'] = False  # 处理负号显示异常# 计算路径距离，即评价函数
def calFitness(line, dis_matrix):dis_sum = 0dis = 0for i in range(len(line)):if i < len(line) - 1:dis = dis_matrix.loc[line[i], line[i + 1]]  # 计算距离dis_sum = dis_sum + diselse:dis = dis_matrix.loc[line[i], line[0]]dis_sum = dis_sum + disreturn round(dis_sum, 1)def traversal_search(line, dis_matrix, tabu_list):# 邻域随机遍历搜索traversal = 0  # 搜索次数traversal_list = []  # 存储局部搜索生成的解,也充当局部禁忌表traversal_value = []  # 存储局部解对应路径距离while traversal <= traversalMax:pos1, pos2 = random.randint(0, len(line) - 1), random.randint(0, len(line) - 1)  # 交换点# 复制当前路径，并交换生成新路径new_line = line.copy()new_line[pos1], new_line[pos2] = new_line[pos2], new_line[pos1]new_value = calFitness(new_line, dis_matrix)  # 当前路径距离# 新生成路径不在全局禁忌表和局部禁忌表中，为有效搜索，否则继续搜索if (new_line not in traversal_list) & (new_line not in tabu_list):traversal_list.append(new_line)traversal_value.append(new_value)traversal += 1return min(traversal_value), traversal_list[traversal_value.index(min(traversal_value))]def greedy(CityCoordinates, dis_matrix):'''贪婪策略构造初始解'''# 出来dis_matrixdis_matrix = dis_matrix.astype('float64')for i in range(len(CityCoordinates)): dis_matrix.loc[i, i] = math.pow(10, 10)line = []  # 初始化now_city = random.randint(0, len(CityCoordinates) - 1)  # 随机生成出发城市line.append(now_city)  # 添加当前城市到路径dis_matrix.loc[:, now_city] = math.pow(10, 10)  # 更新距离矩阵，已经过城市不再被取出for i in range(len(CityCoordinates) - 1):next_city = dis_matrix.loc[now_city, :].idxmin()  # 距离最近的城市line.append(next_city)  # 添加进路径dis_matrix.loc[:, next_city] = math.pow(10, 10)  # 更新距离矩阵now_city = next_city  # 更新当前城市return line# 画路径图
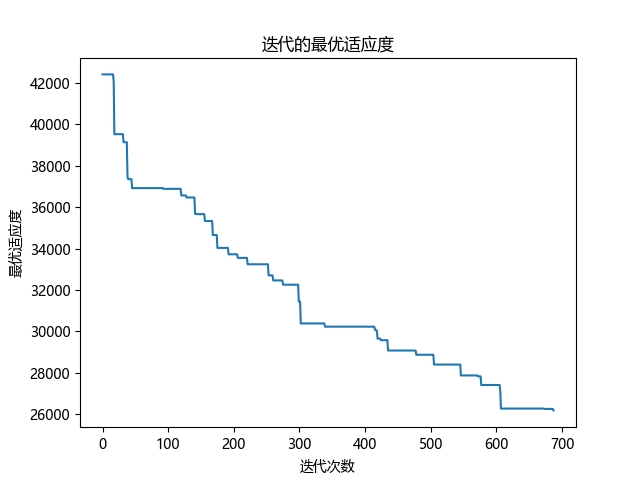
def draw_path(line, CityCoordinates):x, y = [], []for i in line:Coordinate = CityCoordinates[i]x.append(Coordinate[0])y.append(Coordinate[1])for j in range(len(line) - 1):plt.quiver(x[j], y[j], x[j + 1] - x[j], y[j + 1] - y[j], color='r', width=0.005, angles='xy', scale=1,scale_units='xy')plt.quiver(x[-1], y[-1], x[0] - x[-1], y[0] - y[-1], color='r', width=0.005, angles='xy', scale=1,scale_units='xy')plt.title('基于禁忌搜索算法的TSP')# plt.figure()# plt.plot(x, y,color='r', alpha=0.8, linewidth=0.8)# plt.xlabel('x')# plt.ylabel('y')plt.show()if __name__ == '__main__':# 随机生成城市信息nCity = 50CityCoordinates = np.random.uniform(0, 2000, [nCity, 2])  # uniform()生成nCity个二维数组，数值范围是0到2000# 参数设置CityNum = nCity  # 城市数量MinCoordinate = 0  # 二维坐标最小值MaxCoordinate = 101  # 二维坐标最大值tabu_limit = 50  # 禁忌长度，该值应小于(CityNum*(CityNum-1)/2）iterMax = 200  # 迭代次数traversalMax = 100  # 每一代局部搜索次数tabu_list = []  # 禁忌表tabu_time = []  # 禁忌次数best_value = math.pow(10, 10)  # 较大的初始值，存储最优解best_line = []  # 存储最优路径# 计算城市之间的距离dis_matrix = pd.DataFrame(data=None, columns=range(len(CityCoordinates)), index=range(len(CityCoordinates)))for i in range(len(CityCoordinates)):xi, yi = CityCoordinates[i][0], CityCoordinates[i][1]for j in range(len(CityCoordinates)):xj, yj = CityCoordinates[j][0], CityCoordinates[j][1]dis_matrix.iloc[i, j] = round(math.sqrt((xi - xj) ** 2 + (yi - yj) ** 2), 2)# 贪婪构造line = greedy(CityCoordinates, dis_matrix)value = calFitness(line, dis_matrix)  # 初始路径距离# 存储当前最优best_value, best_line = value, linebest_value_list = []best_value_list.append(best_value)# 更新禁忌表tabu_list.append(line)tabu_time.append(tabu_limit)itera = 0while itera <= iterMax:new_value, new_line = traversal_search(line, dis_matrix, tabu_list)if new_value < best_value:  # 优于最优解best_value, best_line = new_value, new_line  # 更新最优解best_value_list.append(best_value)print('第%d次:当前优解为' % (itera+1))print(best_line)line, value = new_line, new_value  # 更新当前解# 更新禁忌表tabu_time = [x - 1 for x in tabu_time]if 0 in tabu_time:tabu_list.remove(tabu_list[tabu_time.index(0)])tabu_time.remove(0)tabu_list.append(line)tabu_time.append(tabu_limit)itera += 1# 路径顺序print("-------最优解为：")print(best_line)# 画路径图draw_path(best_line, CityCoordinates)