【力扣】96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

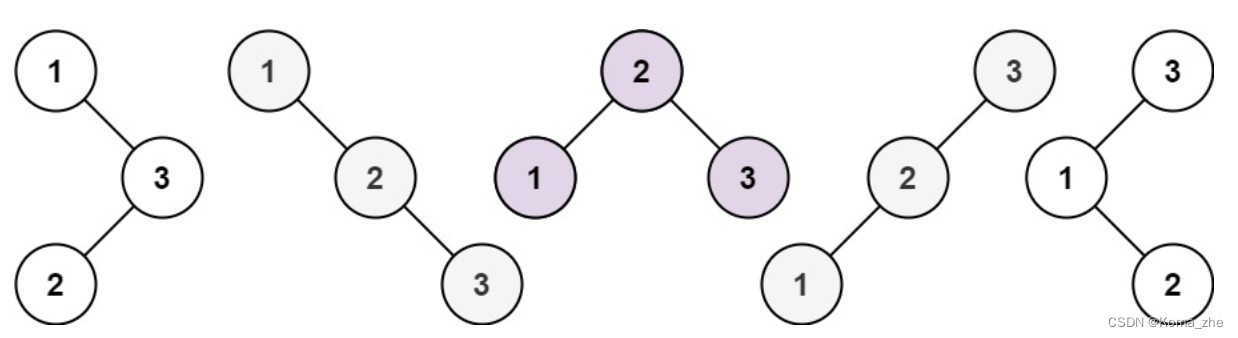
输入：n = 3
输出：5

示例 2：
输入：n = 1
输出：1

提示：
1 <= n <= 19

题解

• 确定 dp 数组以及下标的含义
  dp[i] ： 1到 i 为节点组成的二叉搜索树的个数为 dp[i]
  i 个不同元素节点组成的二叉搜索树的个数为 dp[i]
• 确定递推公式
  dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
  元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
  元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
  元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
  有2个元素的搜索树数量就是 dp[2]。有1个元素的搜索树数量就是 dp[1]。
  所以 dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
  

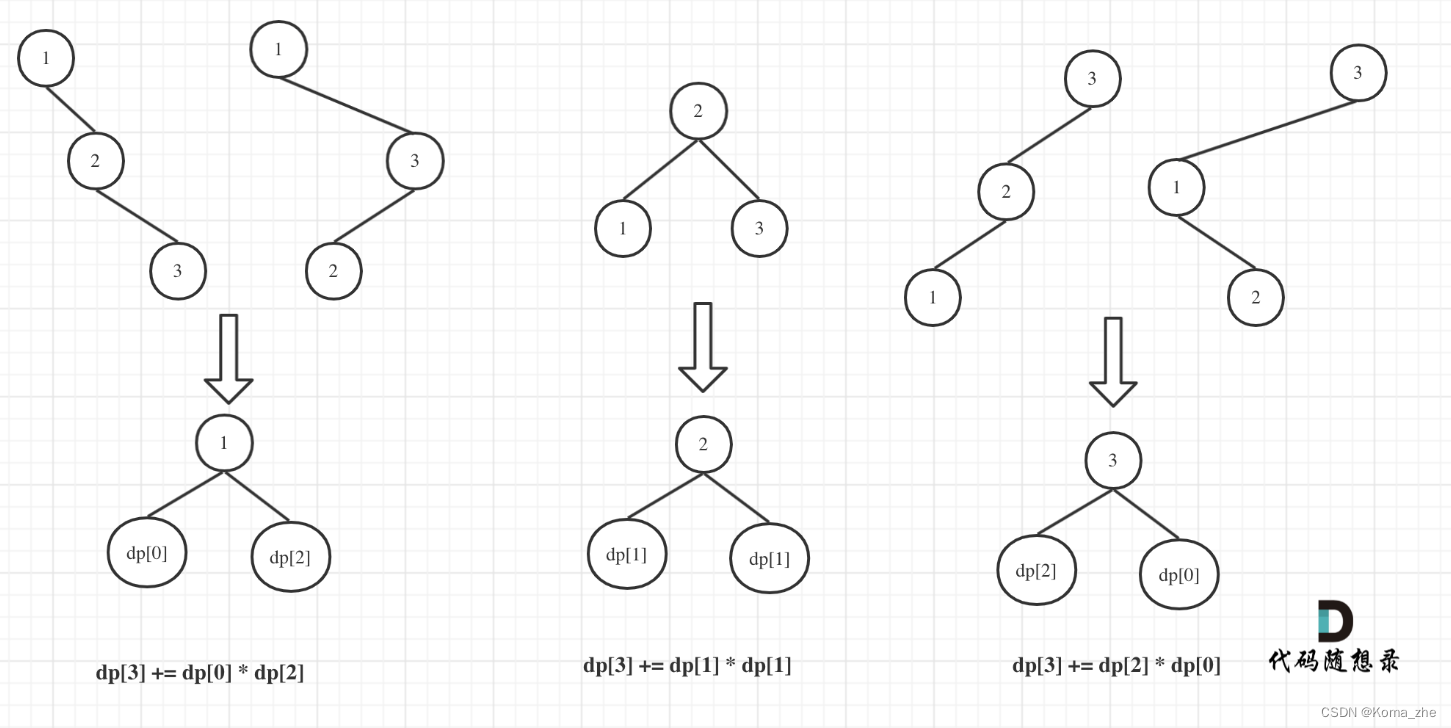
dp[i] += dp[以 1到i-1 为头结点左子树节点数量] * dp[以 i-(1到i-1) 为头结点右子树节点数量]

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为 j 为头结点左子树节点数量，i-j 为以 j 为头结点右子树节点数量。

• dp 数组如何初始化
  dp[0] = 1
• 确定遍历顺序
  节点数为 i 的状态是依靠 i 之前节点数的状态。
  那么遍历 i 里面每一个数作为头结点的状态，用 j 来遍历

for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}

• 举例推导 dp 数组（打印 dp 数组）

class Solution {public int numTrees(int n) {//初始化int[] dp = new int[n + 1];//初始化0个节点和1个节点的情况dp[0] = 1;// 遍历for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {// dp 方程dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
}