一、主成分分析简介
主成分分析(Principal Component Analysis,PCA)是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
在实际问题研究中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的。因此,能否在相关分析的基础上,用较少保留原来变量所反映的信息?保留原来变量所反映的信息?主成分分析应运而出。主成分分析是把原来多个变量划为少数几个综合指标的-种统计分析方法。从数学角度来看,这是一种降维处理技术。
什么是降维?
降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维的优点
- 使得数据集更易使用
- 降低算法的计算开销
- 去除噪声
- 使得结果容易理解
二、适用赛题
主成分分析更像是一种辅助方式,将高维数据转为低维数据,便于结果的描述、呈现。
所以主成分更适合搭配像回归、分类、聚类等模型使用。
三、模型流程

四、流程分析
下面简单给出主成分分析的思想


看到这里是不是有点典型相关分析的影子?
1.标准化处理
首先进行标准化处理


2.计算协方差矩阵
计算刚刚标准化样本的协方差矩阵

1、2步可以直接合并为一步:直接计算x矩阵的样本相关系数矩阵(在相关性模型中讲解过相关函数)。

3.得到特征值和特征向量
计算得到R的特征值和特征向量

在MATLAB中可使用计算特征值和特征向量的函数:eig(R)
4.计算参数
参数有两个,分别是贡献率和累计贡献率
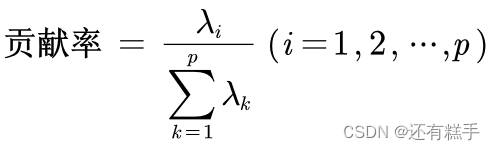

5.得到主成分
一般取累计贡献率超过80%的特征值所对应的第一、第二、.... 、第m(m ≤ p)个主成分。第i个主成分:

6.分析主成分
这个是主成分有难度的地方,我们需要对每一个主成分进行一个合理的解释。对于某个主成分而言,指标前面的系数越大,代表该指标对于该主成分的影响越大。
五、补充
1.主成分分析的说明
在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平,其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释。
主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。因此,提取的主成分个数m通常应明显小于原始变量个数p (除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。
如果原始变量之间具有较高的相关性,则前面少数几个主成分的累计贡献率通常就能达到一个较高水平,也就是说,此时的累计贡献率通常较易得到满足。
主成分分析的困难之处主要在于要能够给出主成分的较好解释,所提取的主成分中如有一个主成分解释不了,整个主成分分析也就失败了。
主成分分析是变量降维的一种重要、常用的方法,简单的说,该方法要应用得成功,一是靠原始变量的合理选取,二是靠“运气”。
------参考教材:《应用多元统计分析》王学民
2.主成分分析的滥用:主成分得分

王老师已在论文中做出了详细的解释。
3.主成分分析适合于哪些
像对于聚类的降维,主成分分析还可以用来解决多重共线性的问题。
4.关于主成分分析的一些问题
问题1:之前学过逐步回归,逐步回归也可以用来解决多重共线性问题,那么该用逐步回归还是主成分分析呢?
答:如果能够很好的解释清楚主成分代表的含义,那么建议你在正文中既用主成分分析,又用逐步回归(多分析点没啥坏处,只要你能保证你不分析错就行),如果你解释不清楚,那么还是用逐步回归吧。
问题2:主成分回归后,需要将原来的变量带回到回归方程吗?
答:没必要,要是带回去了,那和普通的回归有什么区别呢。主成分的核心作用就是降维,带回去了维度也没降下来呀。
------参考回答:清风









)







2024最新汉化注册补丁包下载)

