我们的心永远向前憧憬

尽管活在阴沉的现在        

一切都是暂时的,转瞬即逝,

而那逝去的将变为可爱

                                                                                   🌝(俄) 普希金 <假如生活欺骗了你>

1.二叉搜索树的概念

概念:搜索树（Search Tree）是一种有序的数据结构，用于存储和组织一组元素。它提供高效的搜索、插入和删除操作。

组成:搜索树是由节点（Node）组成的树状结构，每个节点包含一个关键字（Key）和相关的数据（Data）。通过比较节点的关键字，可以确定元素在搜索树中的位置。

常见的搜索树包括二叉搜索树（Binary Search Tree）和平衡二叉搜索树（Balanced Binary Search Tree），如红黑树（Red-Black Tree）、AVL树等。

本篇文章主要讲的是二叉搜索树

在二叉搜索树中，每个节点最多有两个子节点，且左子节点的关键字小于父节点的关键字，右子节点的关键字大于父节点的关键字。这种有序性质使得在搜索树中进行搜索操作时，可以通过比较关键字的大小来决定搜索方向，从而快速地找到目标元素,简而言之如下:

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

 比如有一组数组:

int array[] = {{5,3,4,1,7,8,2,6,0,9}

则它的二叉搜索树为:

---

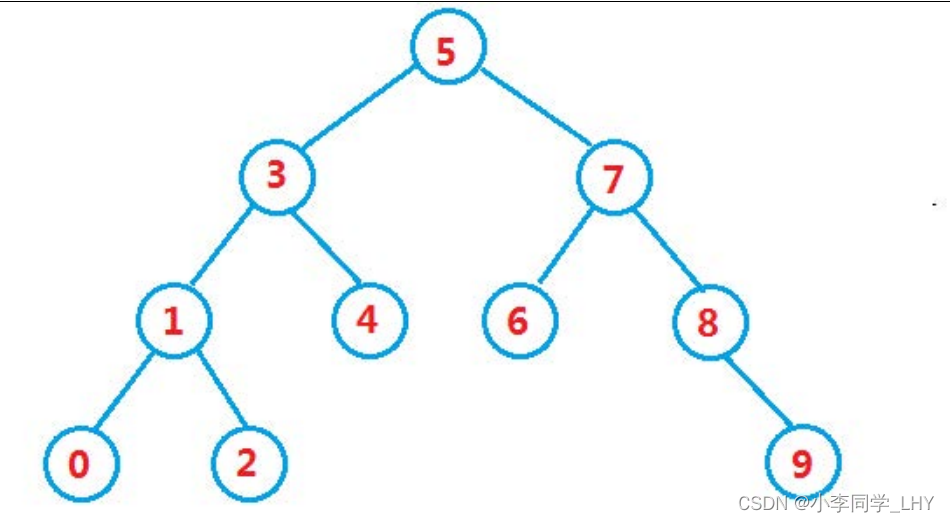
2.二叉搜索树的定义类

public class BinarySearchTree {static class TreeNode{public int val;//元素public TreeNode left;//左子树public TreeNode right;//右子树public TreeNode(int val){this.val = val;}}public TreeNode root;
}

3.实现二叉搜索树的查找

执行步骤:

1. 从root根节点开始，将要查找的关键字与当前节点的关键字进行比较。
2. 如果要查找的key关键字等于当前节点的关键字，则找到了目标元素，查找成功。
3. 如果要查找的key关键字小于当前节点的关键字，则继续在当前节点的左子树中进行查找。
4. 如果要查找的key关键字大于当前节点的关键字，则继续在当前节点的右子树中进行查找。
5. 如果当前节点的左子树或右子树为空，表示查找失败，目标元素不存在于树中。
6. 重复步骤1-5，直到找到目标元素或确定目标元素不存在。

例子解释:

现在有一组数据:查找关键字8

int array[] = {{5,3,4,1,7,8,2,6,0,9}

逻辑思路:

1. 初始化一个指针，将其指向根节点，例如使用cur指针，并将其初始值设置为根节点。
2. 进入一个循环，循环条件是当前节点不为空，即cur不为null。
3. 在循环中，比较当前节点的关键字与目标关键字的大小关系。
4. 如果当前节点的关键字小于目标关键字，说明目标元素应该在当前节点的右子树中，将当前节点指针cur移动到右子节点，即cur = cur.right。
5. 如果当前节点的关键字大于目标关键字，说明目标元素应该在当前节点的左子树中，将当前节点指针cur移动到左子节点，即cur = cur.left。
6. 如果当前节点的关键字等于目标关键字，表示已经找到了目标元素，可以返回true或执行其他相应的操作。
7. 如果循环结束仍然没有找到目标元素，即当前节点为空，表示查找失败，可以返回false或执行其他相应的操作。

如视频展示:

代码如下:

public boolean search(int key){TreeNode cur = root; // 初始化当前节点指针cur为根节点rootwhile(cur != null){ // 循环条件：当前节点cur不为空if(cur.val < key){ // 如果当前节点的值小于目标关键字keycur = cur.right; // 移动当前节点指针cur到右子节点}else if(cur.val > key){ // 如果当前节点的值大于目标关键字keycur = cur.left; // 移动当前节点指针cur到左子节点}else {return true; // 当前节点的值等于目标关键字key，找到了目标元素，返回true}}return false; // 循环结束仍然没有找到目标元素，返回false，表示查找失败
}

时间复杂度：

• 平均情况下，二叉搜索树的查找操作时间复杂度为O(log n)，其中n是二叉搜索树中的节点数。每次比较都可以将搜索范围缩小一半。
• 最坏情况下(只有左子树或右子树)，如果二叉搜索树是非平衡树，查找操作的时间复杂度可能达到O(n)，其中n是二叉搜索树中的节点数。树的结构类似于链表，需要遍历从根节点到叶子节点的路径。

空间复杂度：

• 在迭代方式的二叉搜索树查找中，只使用了常数级别的额外空间，即只有一个额外的指针用于保存当前节点的引用，因此空间复杂度为O(1)。

---

4.实现二叉搜索树的插入

执行步骤:

1. 首先，检查根节点root是否为空。如果为空，表示该二叉搜索树为空树，将新节点TreeNode(val)作为根节点插入，并返回true表示插入成功。
2. 如果根节点不为空，初始化当前节点指针cur为根节点root，父节点指针parent为null。
3. 进入循环，条件为当前节点cur不为空。
4. 在循环中，比较当前节点cur的值与待插入值val的大小关系：
5. 循环结束后，表明找到了合适的插入位置。创建新节点TreeNode(val)。
6. 判断父节点parent的值与待插入值val的大小关系：
7. 返回true，表示插入成功。

视频展示如下:

代码如下:

public boolean insert(int val){if(root == null){ // 如果根节点为空，将新节点作为根节点插入root = new TreeNode(val);return true;}TreeNode cur = root; // 初始化当前节点指针cur为根节点rootTreeNode parent = null; // 初始化父节点指针parent为空while(cur != null){ // 循环条件：当前节点cur不为空if(cur.val < val){ // 如果当前节点的值小于待插入值valparent = cur; // 更新父节点指针为当前节点cur = cur.right; // 移动当前节点指针cur到右子节点} else if (cur.val > val) { // 如果当前节点的值大于待插入值valparent = cur; // 更新父节点指针为当前节点cur = cur.left; // 移动当前节点指针cur到左子节点} else{ // 如果当前节点的值等于待插入值val，即已存在相同值的节点return false; // 返回false，表示插入失败（不允许插入重复值）}}TreeNode node = new TreeNode(val); // 创建新节点if(parent.val > val){ // 如果父节点的值大于待插入值valparent.left = node; // 将新节点插入为父节点的左子节点}else {parent.right = node; // 将新节点插入为父节点的右子节点}return true; // 返回true，表示插入成功
}

时间复杂度：
在最坏情况下，即二叉搜索树是一个非平衡树的情况下，插入操作的时间复杂度为O(n)，其中n是二叉搜索树中的节点数。这种情况下，树的结构类似于链表，每次插入都需要遍历从根节点到叶子节点的路径。

在平均情况下，二叉搜索树的插入操作的时间复杂度为O(log n)，其中n是二叉搜索树中的节点数。每次插入操作都可以将搜索范围减半，因此插入操作的时间复杂度是对数级别的。

空间复杂度：
在二叉搜索树的插入操作中，只需要使用常数级别的额外空间，即只有几个指针变量用于保存当前节点和父节点的引用。因此，插入操作的空间复杂度为O(1)。

---

5.实现二叉搜索树的删除

具体删除操作分三种情况:

第一种情况：待删除节点cur没有左子节点。

• 如果cur是根节点，直接将根节点指向其右子节点cur.right。
• 如果cur是父节点parent的左子节点，将父节点的左子节点指向cur.right。
• 如果cur是父节点parent的右子节点，将父节点的右子节点指向cur.right。

视频展示:

第二种情况：待删除节点cur没有右子节点。

• 如果cur是根节点，直接将根节点指向其左子节点cur.left。
• 如果cur是父节点parent的左子节点，将父节点的左子节点指向cur.left。
• 如果cur是父节点parent的右子节点，将父节点的右子节点指向cur.left。

视频展示

第三种情况：待删除节点cur既有左子节点又有右子节点。

注意:待删除结点的数据将来放的数据一定是比左边都大,比右边都小的数据
如何寻找数据?
要么在左树里面找到最大的数据[即左树最右边的数据]

要么在右树里面找到最小的数据[即右数最左边的数据]

下面我使用的是在右数找最小值

执行步骤:

• 找到待删除节点cur的右子树中的最小节点target，即右子树中最左侧的节点。
• 将最小节点target的值赋给待删除节点cur，相当于将cur节点的值替换为target节点的值。
• 删除最小节点target，即对最小节点target执行第一种或第二种情况的删除操作。

视频展示: 

注意:

当target没有左孩子时,应当时targetParent.right == target.right

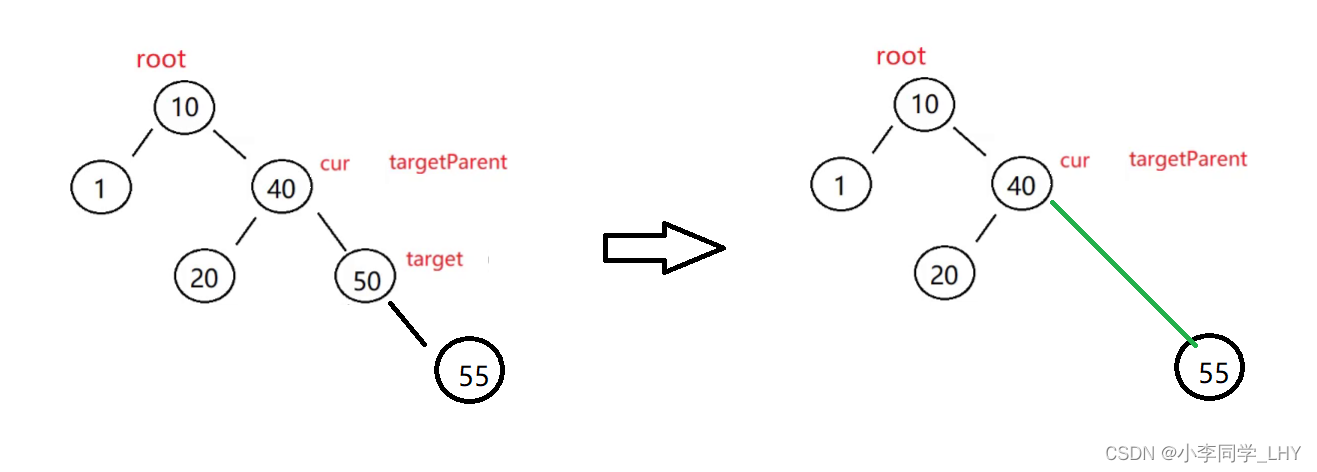
代码如下:

public void remove(int key){TreeNode cur = root; // 初始化当前节点指针cur为根节点rootTreeNode parent = null; // 初始化父节点指针parent为空while(cur != null){ // 循环条件：当前节点cur不为空if(cur.val < key){ // 如果当前节点的值cur.val小于待删除值keyparent = cur; // 更新父节点指针parent为当前节点curcur = cur.right; // 将当前节点指针cur移动到右子节点cur.right} else if (cur.val > key) { // 如果当前节点的值cur.val大于待删除值keyparent = cur; // 更新父节点指针parent为当前节点curcur = cur.left; // 将当前节点指针cur移动到左子节点cur.left} else { // 当前节点的值cur.val等于待删除值key，找到待删除节点removeNode(cur, parent); // 调用removeNode函数执行删除操作}}
}private void removeNode(TreeNode cur, TreeNode parent) {// 第一种情况：待删除节点cur没有左子节点if(cur.left == null){if(cur == root){ // 如果待删除节点cur是根节点root = cur.right; // 直接将根节点指向其右子节点cur.right} else if (cur == parent.left) { // 如果待删除节点cur是父节点parent的左子节点parent.left = cur.right; // 将父节点的左子节点指向cur.right} else { // 如果待删除节点cur是父节点parent的右子节点parent.right = cur.right; // 将父节点的右子节点指向cur.right}}// 第二种情况：待删除节点cur没有右子节点else if(cur.right == null){if(cur == root){ // 如果待删除节点cur是根节点root = cur.left; // 直接将根节点指向其左子节点cur.left} else if(cur == parent.left){ // 如果待删除节点cur是父节点parent的左子节点parent.left = cur.left; // 将父节点的左子节点指向cur.left} else { // 如果待删除节点cur是父节点parent的右子节点parent.right = cur.left; // 将父节点的右子节点指向cur.left}}// 第三种情况：待删除节点cur既有左子节点又有右子节点else {TreeNode targetParent = cur; // 初始化目标节点的父节点指针为curTreeNode target = cur.right; // 初始化目标节点指针为cur的右子节点while(target.left != null){ // 寻找cur右子树中的最小节点targetParent = target; // 更新目标节点的父节点指针为targettarget = target.left; // 将目标节点指针移动到左子节点target.left}cur.val = target.val; // 将目标节点的值赋给待删除节点cur，相当于替换值if(targetParent.left == target){ // 如果目标节点是其父节点的左子节点targetParent.left = target.right; // 将目标节点的右子节点连接到目标节点的父节点的左子节点上} else { // 如果目标节点是其父节点的右子节点targetParent.right = target.right; // 将目标节点的右子节点连接到目标节点的父节点的右子节点上}}
}

时间复杂度：

• 在平均情况下，二叉搜索树的高度为O(log N)，其中N是树中节点的总数。在删除节点的过程中，需要遍历树以找到待删除节点的位置，这需要沿着树的高度移动。因此，平均情况下删除节点的时间复杂度为O(log N)。
• 在最坏情况下，如果二叉搜索树是一个不平衡的树，即所有节点都只有一个子节点，删除节点的时间复杂度可以达到O(N)，其中N是树中节点的总数。这种情况发生在树没有进行平衡操作或者插入和删除操作导致树失去平衡的情况下。

空间复杂度：

• 删除节点的过程中使用了常数级别的额外空间，主要是用于存储当前节点指针cur和父节点指针parent。因此，删除节点的空间复杂度为O(1)。

 6.总结

• 二叉搜索树的查找、插入和删除操作都是基于节点值的比较来进行的。
• 查找操作的时间复杂度为O(log N)，其中N是树中节点的总数。插入和删除操作的时间复杂度也是O(log N)，但在最坏情况下（树不平衡），时间复杂度可能达到O(N)。
• 二叉搜索树的插入和删除操作可以保持树的有序性，但如果插入和删除操作频繁且不平衡，可能会导致树的高度增加，降低操作效率。
• 为了解决不平衡问题，可以使用平衡二叉搜索树（如AVL树、红黑树）等数据结构来保持树的平衡性，以提高查找、插入和删除操作的性能。

---

结语:

二叉搜索树提供了一种简洁而强大的数据结构，它不仅仅是一棵树，更是一种思想。通过理解和应用二叉搜索树的原理，我们可以解决各种问题，如数据的排序、查找最小/最大值、范围查询等。

在结束之际，让我们怀着对二叉搜索树的敬意，继续探索和学习更多的数据结构和算法，为解决复杂的计算问题开辟新的道路。无论是在计算机科学的领域中，还是在生活的各个方面，二叉搜索树的智慧将继续指引我们前行。