在今年1月2日和1月3日,旅游板块两支个股先后涨停,此后一支月内三倍,另一支连续6个涨停。事后复盘,我们如何在1月2日第一支个股涨停之后,通过量化分析,找出第二支股?
一个3倍,一个6连板
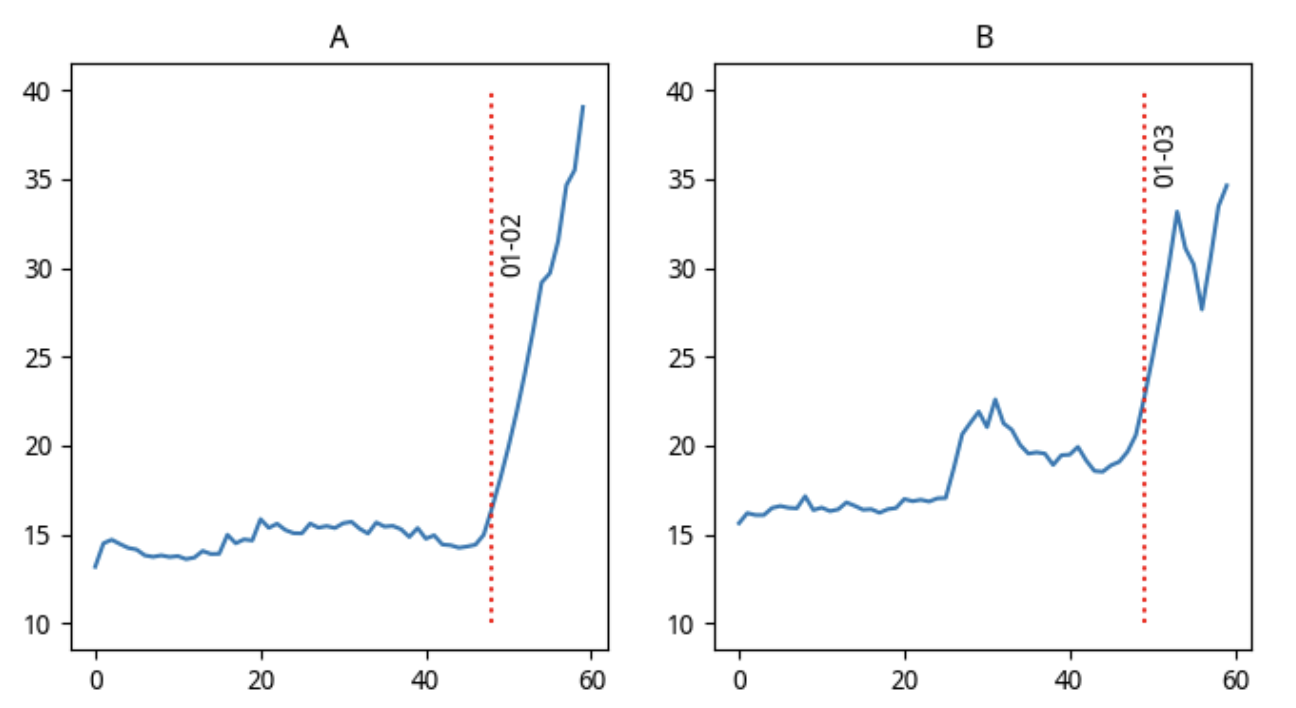
这是两支个股在2024年1月17日前60日收盘价图。图中红色虚线是个股启动时间。A大概是受董宇辉小作文、或者尔滨旅游热题材发酵带动,于1月2日率先启动。
尽管A在半个月内股价接近3倍,但从量化的角度,目前还难以精准地实现事件驱动上涨这种类型的建模。但是,如果我们在A启动之后,在1月2日收盘前买入B(就这次而言,B次日开盘仍有买入机会),连续收获6个涨停,也完全可以满意。
现在,我们就来复盘,如何从A涨停,到发现B。
首先,运行策略的时间应该放在14:30分之后,此时对市场进行扫描,找出首板涨停的个股。当日涨停数据在Akshare可以获得,印象中,它能区分首板涨停和连板。
对首板涨停的个股,我们先获取它所在的概念板块。然后对每个板块的成员股进行遍历,通过相关性分析,找到关联度较高的个股。

如果仅仅是和龙头同在一个板块是无法保证资金眷顾的。而且,一支个股往往身兼多个概念,在极短的时间里要弄清楚究竟是炒的它的哪一个概念也不容易。不过,通过数据挖掘,我们可以完全不去理会炒作背后的逻辑 – 何况很多逻辑,根本就是狗p不通。
我们用相关性检测来进行数据挖掘。
相关系数
在概率论和统计学中,相关性(Correlation)显示了两个或几个随机变量之间线性关系的强度和方向。
通常使用相关系数来计量这些随机变量协同变化的程度,当随机变量间呈现同一方向的变化趋势时称为正相关,反之则称为负相关。
我们通过以下公式来计算两个随机变量之间的相关性:
ρ X Y = c o v ( X , Y ) σ X σ Y \rho_{XY} = \frac{cov(X, Y)}{\sigma_X\sigma_Y} ρXY=σXσYcov(X,Y)
这样定义的相关系数称作皮尔逊相关系数。一般我们可以通过numpy中的corrcoef,或者scipy.stats.pearsonr来计算。
下面的代码演示了正相关、负相关和不相关的例子:
# x0与x1正相关, 与x2负相关, 与x3分别为不同的随机变量
x0 = np.random.normal(size=100)
x1 = 10* x0 + 1
x2 = -10 * x0 + 1
x3 = np.random.normal(size=100)x = np.vstack((x0, x1, x2, x3))
rho = np.corrcoef(x)fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12, 3))for i in [0,1,2]:ax[i].scatter(x[0,],x[1+i,])desc = "Pearson: {:.2f}".format(rho[0,i+1])ax[i].title.set_text(desc)ax[i].set(xlabel='x',ylabel='y')plt.show()
绘图时,我们以 x 0 x_0 x0为x轴,以 x i x_i xi为y轴,如果 x 0 x_0 x0与 x 1 x_1 x1完全正相关,那么将绘制出一条 4 5 。 45^。 45。向上的直线。这其实就是QQ-Plot的原理。
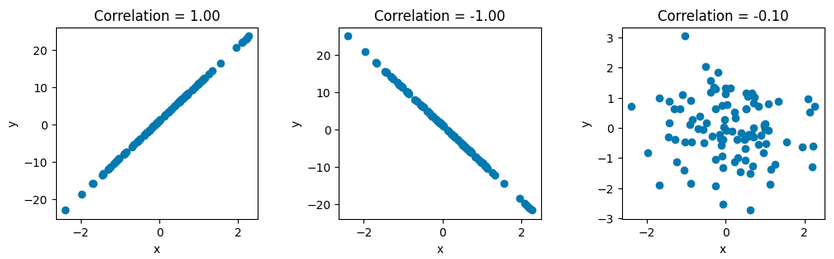
从左图过渡到右图,只需要在 x 0 x_0 x0中不断掺入噪声即可。读者可以自己尝试一下。
皮尔逊相关系数要求只有变量之间是线性相关时,它才能发现这种关联性。很多时候我们必须放宽条件为:标的A上涨,则B也跟着涨。但不管A涨多少,B跟涨又是多少,都不改变它们联系的强度。此时,就要用Spearman相关性。

上面的例子演示的是皮尔逊相关系数的求法,这里使用的是np.corrcoef。它的结果是一个矩阵,所以上例中的变量rho,其取值实际上是:

在这个矩阵中,对角线上的值是自相关系数,显然它们都应该为1。实际上我们要得到时间序列 s 1 s_1 s1和 s 2 s_2 s2之间的相关系数,应该取 ρ [ 0 ] [ 1 ] \rho[0][1] ρ[0][1],对 s 1 s_1 s1和 s 3 s_3 s3之间的相关系数,应该取 ρ [ 0 ] [ 2 ] \rho[0][2] ρ[0][2],依次类推,这些可以在代码第13行看到。
我们通过scipy.stats.spearmanr来计算Spearman相关。我们将通过真实的例子来进行演示。
发现强相关个股
假设我们已经拿到了概念板块的个股名单。现在,我们两两计算它们与龙头个股之间的相关性,如果相关系数在0.75以上,我们就认为是强相关,纳入备选池。
相关系数是一个无量纲的数,取值在[-1,1]之间。因此,可以把0.75看成具有75分位的含义
async def qqplot(x, y, n=60, end):xbars = await Stock.get_bars(x, n, FrameType.DAY, end=end )ybars = await Stock.get_bars(y, n, FrameType.DAY, end=end)xclose = xbars["close"]yclose = ybars["close"]pearson = scipy.stats.pearsonr(xclose, yclose)[0]spearman = scipy.stats.spearmanr(xclose, yclose).statisticif pearson < 0.75:returna, b = np.polyfit(xclose, yclose, 1)ax = plt.subplot(1,1,1)ax.scatter(xclose, yclose)ax.plot(xclose, a * xclose + b)namex = await Security.alias(x)namey = await Security.alias(y)ax.title.set_text(f'{namex} <=> {namey} pearson: {pearson:.2f} spearman: {spearman:.2f}')plt.show()
假设现在是1月2日的下午2时,已经能确认标的A不会开板。现在,我们就拿它与板块内的其它个股逐一计算相关性,排除掉弱相关的个股,因为,既然是弱相关,那么它们就不会跟涨,也不怎么跟跌(在我A,跟跌是必须的)。
当我们使用 pearson > 0.75的判断条件时,在该板块的22支个股中,筛选出5支个股。如果使用spearman > 0.75来判断,则只会选出4支,并且这4支都在pearson筛选出的范围内。这里为排版美观起见,只给出共同的4支:
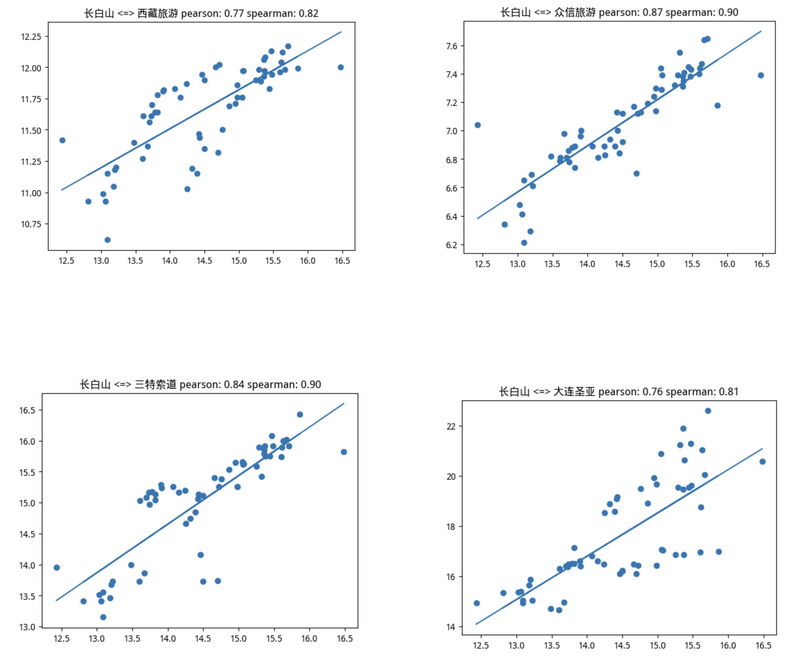
很幸运,我们要找的标的正在其中。
你肯定想知道另外三支的结果如何。它们有连板吗?有大幅下跌吗?
没有下跌。别忘了,我们是通过相关系数选出来的标的,只要这种关联还存在,即使不跟随上涨,也不应该大幅下跌,不是吗?
实际上,有一支在我们讨论的区间里持平,一支上涨5%,另一支最高上涨16.9%。但如果你有更高的期望,在这个case中,一点点看盘经验可以帮助我们过滤掉另外两只,最终,我们会买入上涨16.9%和6连板的股票。
这个看盘经验是,不要买上方有均线,特别是中长均线的股。这种股在上攻过程中,将会遇到较大的抛压。如果一个很小的板块,资金已经有了一到两个进攻的标的了,是不会有多余的钱来关照这些个股的。
这个策略还有一个很好的卖出条件。如果龙头股一直保持上涨,而个股的关联系数掉出0.75,显然,我们可以考虑卖出。如果龙头股出现滞涨(开盘半小时内不能封住),则也是离场时机。
这一篇我们讨论的是同一板块个股的相关性。如果是处在上下游的两个板块,它们也可能存在相关性,但会有延时。这种情况称作cross correlation。它应该如何计算,又如何使用,也许后面我们会继续探索。












——点亮LED)


)

通信技术)

】)