据说勾股定理约有500种证明方法，下面介绍几种经典的证明方法。
一、切割重拼法。
顾名思义，就是将图形切割成其他形式的图形，然后通过拼图转换为另一种图形，这个过程中图形的面积是不变的。
“赵爽弦图”是这种方法的经典应用，它是我国汉代的赵爽在注解《周髀算经》时给出的。
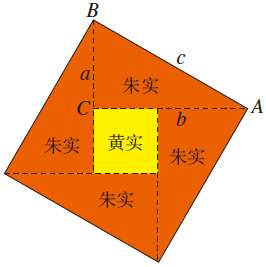
这个图是真正的集美貌与智慧于一身，赵老师把四个一样的直角三角形（红色）围成了一个大正方形，中空的部分是一个小正方形（黄色）。
面积就是一小块实地，所以他把红色图形的面积叫“朱实”，黄色图形的面积叫“黄实”。
赵老师指出：按弦图，又可以勾股相乘为朱实二，倍之为朱实四。以勾股之差自相乘为中黄实。加差实，亦成弦实。
这段话其实给出了一个证明勾股定理的方法：用“拼图+代数”的方法证明。
我们都听说过“勾三股四弦五”，“勾”就是直角三角形的短边，“股”是长边，“弦”是斜边。
设红色直角三角形的面积为 ，“勾股相乘为朱实二，倍之为朱实四”就是
，
。
设黄色正方形的面积为
，“以勾股之差自相乘为中黄实”就是
。
设大正方形的面积为S，“加差实，亦成弦实”就是
。
代入得：
，解得
。
这种证法是不是也很简单呢？
但是赵老师用的不是这种证法，而是用了另外一种更巧妙的证明方法，就是咱们开头说的“切割重拼法”。
证明过程如下：
把边长为a、b的两块正方形木板边挨边对齐，用哥俩好将接缝处粘牢。按下图画线、上色，将整块木板分为四个一样的直角三角形（红色）和一个正方形（黄色）。沿下图斜线将木板切开。
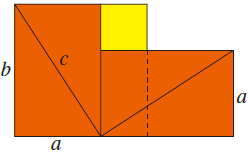
将切下的两个红色直角三角形以一个华丽的转身移至图形上方如图位置，再用哥俩好粘牢。
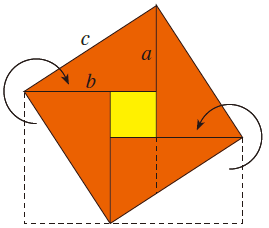
最后形成这样一个优美的图形，它就是“赵爽弦图”。整个图形由原来的以a、b为边长的两个正方形变成一个以直角三角形斜边c为边长的正方形。
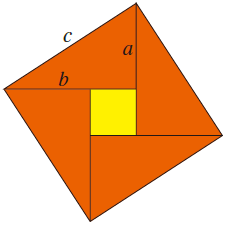
好了，整个过程就是一次手工制作，至此咱们已经完成了勾股定理的证明。
是的，证明完了，几乎不需要多余的解释。下面的文字描述与如此精妙的方法比起来显得那样的苍白无力：
原来两个正方形的面积和为
，“切割重拼”后形成的大正方形面积是
，整个过程面积未发生改为，所以
。
二、拼图法
就是用几个基本图形拼成另一个图形，七巧板就是这个玩法。
传说毕达哥拉斯就是用这种方法证明的勾股定理，而且用的也是七巧板（只是形状与常规的七巧板不同）
他的七巧板由4个一样的直角三角形、3个以直角三角形三条边为边长的正方形组成。
他把七巧板分别拼成了下图两种形状，
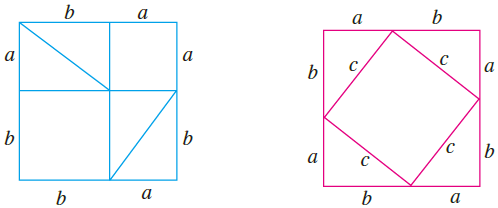
这种证法也不需要代数证明，拿眼睛一扫就明白了。
左右两个大正方形面积相等，它们都有4个一样的三角形，所以左图两个小正方形的面积之和与右图小正方形的面积相等，真可谓巧也妙哉！
这个证法也很简单，但与“赵爽弦图”相比不够纯粹，因它是有“赘肉”的，4个三角形就是“赘肉”。
三、拼图法+代数法
前面在讲“赵爽弦图”时已经提到一次这种证法。这种证法在拼图的基础上，需要用代数式进行证明。
1. 正方形拼图法：毕达哥拉斯图的代数证明法。
直接用上面毕达哥拉斯证法的第二张图证明。
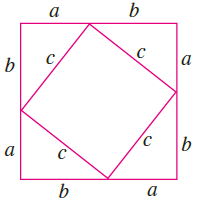
显而易见：４个三角形的面积＋小正方形的面积＝大正方形的面积。
即：
解得：
2. 梯形拼图法：美国第20任总统茄菲尔德（Garfield）的证法。
将两个一样的直角三角形一个横放，一个竖放，使两个三角形一个端点重合，一条边共线。然后将两个直角三角形的另两个端点连线（图中AE），使整个图形形成一个梯形。
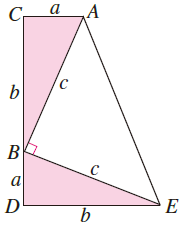
或者也可以这样描述：将两个一样的直角三角形和一个以上述直角三角形斜边c为腰的等腰直角三角形拼成一个梯形。
显然：３个三角形的面积之和＝梯形的面积。
即：
解得：
四、三角形全等法
前面的几种证法都是初中数学教材里提到的，作为中学生一定要搞明白。
下面再介绍一种经典证法，运用到了辅助线和三角形全等，初中生应该掌握。
大家可能都见过下面这种图形，它像一颗树一样，因此被称为“勾股树”。
这颗树的生长规则就是勾股定理：分别以直角三角形的三条边为边长做3个正方形，两个小正方形的面积之和等于大正方形的面积。
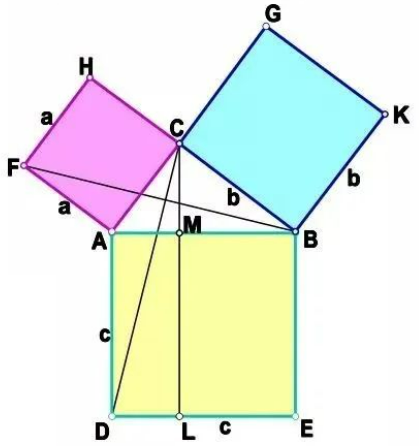
下面介绍的是欧几里得证明法，就是基于上面的这种图形证明的。
首先作3条辅助线：连接BF、CD，过C作CL⊥DE，交AB于点M，交DE于点L。
∵ AF=AC，AB=AD，∠FAB=∠CAD
∴ △FAB≌△CAD
∵ △FAB的面积等于
（AF为底，AC为高，值均为a），△CAD的面积等于矩形ADLM面积的一半（AC为底，AM为高）。
∴ 矩形ADLM面积=
同理可证，矩形MLEB的面积=
∵ 正方形ADEB的面积=矩形ADLM的面积 + 矩青菜MLEB的面积，且正方形ADEB的面积=
∴ 
四、相似三角形法
这种证法的优点就是图形最简洁，只用一个直角三角形外加一根垂线。
证明过程如下：
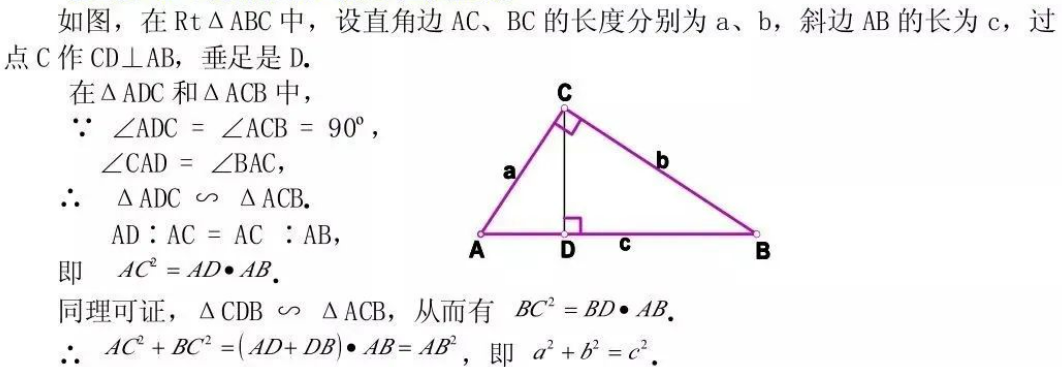
以上共介绍7种勾股定理的证明方法，可谓个个经典，对于初中生来说，应力求全部掌握。对数学感兴趣的朋友，也宜好好研究一下体会其中妙处。
)
)
