77.组合

思路:如果暴力解,需要几个数则需要相应的for循环个数。

回溯法:把数的组合抽象成一颗树,利用递归的思想进行回溯,递归必有回溯。每次遍历到叶子节点,则存入结果。

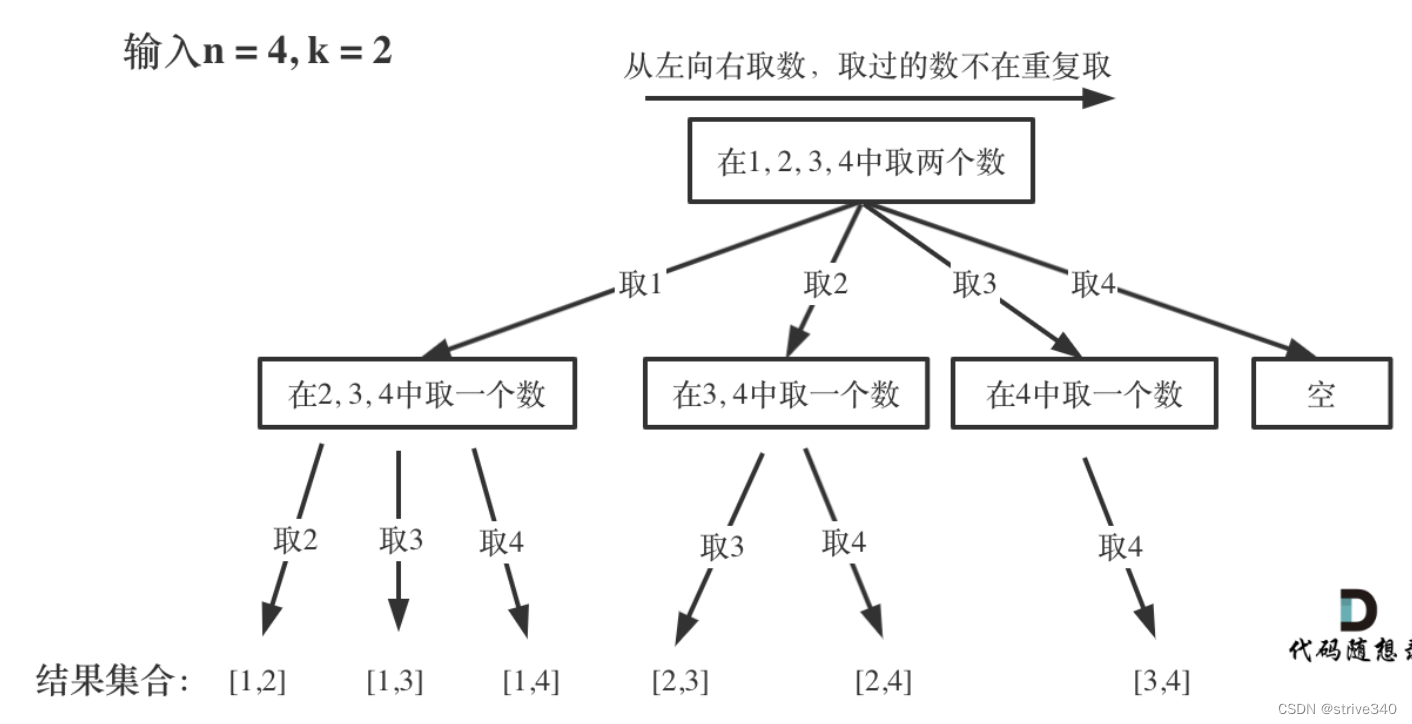
代码：

vector<vector<int>> result;//存放结果vector<int> path;//存放当前进行到的路径void backtracking(int n,int k,int startIndex){//startIndex控制起始位置到末尾的集合大小,逐步缩小集合if(path.size() == k){//当前遍历到了叶节点,把路径加入结果并且返回上一节点result.push_back(path);return;}for(int i = startIndex;i <= n;i++){//遍历当层横向的节点path.push_back(i);backtracking(n,k,i+1);path.pop_back();//回溯}}vector<vector<int>> combine(int n, int k) {result.clear();path.clear();backtracking(n,k,1);return result;}

剪枝优化:假如n=4,k=3。所以数组为1，2，3，4中选取3个数的所有组合。当第一个选取3的时候，当时后面仅有4可选,不满足3个数的组合条件，这种情况如上代码还会进行一步递归，所以这种情况是可以优化的。当起点选为2的时候,这是最后满足条件的起点,当在这一步的时候往后就不需要再递归遍历了。所以k-path.size()是当前还需要找几个元素,n-(k-path.size())如果为正说明后面的元素个数满足还需要找的元素个数。+1则是因为当前不包括startIndex。例如path中没有元素,size为0,则利用这个公式算出为2.指最多到2就可以停下遍历了，后面再遍历也不够元素个数。

for循环条件更改代码：

for(int i = startIndex;i <= n - (k - path.size()) + 1;i++){path.push_back(i);backtracking(n,k,i+1);path.pop_back();}