声明:本系列博客参考有关专业书籍,截图均为自己实操,仅供交流学习!
一、控制系统基本概念
这里就不再介绍类似于开环系统、闭环系统等基本概念了!
1、数学模型
控制系统的数学模型是指动态数学模型,大致可以分为输入输出模型、状态空间模型、结构图模型三种。
①输入输出模型:微分方程模型、传递函数模型、频率特性模型(由传递函数s替换jw得到)。
②状态空间模型:是一种应用更为广泛的数学模型,可用于非线性系统、多变量系统,利用计算机方便获得数值响应。传递函数的状态空间不具唯一性(传递函数不可完全表示控制系统,只可表示处可控部分,而状态空间模型既可表示可控部分也可表示不可控部分。)
③结构图:串联、并联、反馈。
控制系统的性能指标:超调量、调节时间、峰值时间、上升时间。
2、分析方法
①时域分析法:拉普拉斯变换(传递函数)
- 时域响应:单位脉冲、单位阶跃、单位斜坡、单位加速度、单位正弦响应等。
- 稳定性分析:只要存在实部为正的特征根,系统就不稳定。Matlab的zpk和roots函数
②根轨迹分析法:系统某个参数(常为开环增益K)从0到无穷大变化,描绘所有根在S平面的轨迹。
- 幅值条件和相角条件:同时满足这两个条件就是特征方程的根。
- 根轨迹绘制:Matlab的rlocus函数,调节实轴虚轴比例尺相同用axis equal函数。
③频域分析法:频率特性反映的是系统对正弦输入信号的响应性能,可得定性或定量结论。
- 频率响应曲线:奈奎斯特曲线(极坐标图)、伯德图(对数坐标图)、尼科尔斯图(对数幅相图)。尼科尔斯图是将伯德图的2张对数幅频特性和相频特性图在角频率w为参量情况下合成一张图。Matlab的nyquist、bode、nichols函数。
- 频域性能指标:(静态特性)谐振峰值、谐振频率、频带、零频。
- 稳定性分析:奈奎斯特盘踞(当w从负无穷到正无穷变化时,奈奎斯特曲线逆时针包围(-1,j0)的次数N等于系统位于右半平面的极点数P)
- 稳定裕度:增益裕度、相角裕度。Matlab的margin函数。
④状态空间分析法:现代控制论,更全面更广泛!
- 状态空间表示:u输入向量、x状态向量、y输出向量、A系统内部状态系数矩阵、B输入对状态的作用矩阵、C输出与状态的关系矩阵、D输入直接对输出的作用矩阵。Matlab的ss、tf2ss、zp2ss函数。
- 标准型:同一系统、同一传递函数的状态空间模型各种各样,但独立的状态变量个数相同,说明不同状态空间模型之间存在联系——线性变换,变换矩阵P不唯一,所以状态空间模型不唯一。一般有可控标准型、可观标准型、对角标准型、约当标准型。Matlab的canon函数、jordan函数等。
- 稳定性分析:Lyapunov第二方法。Matlab的lyap函数、lyap2函数可求解Lyapunov方程。
二、控制系统仿真模块
控制系统仿真所需模块大部分在Simulink标准仿真子模块库,另外一小部分在专家子模块库(工具箱)。
1、标准模块库
线性系统模块和非线性系统模块,在Continuous子模块库、Discontinuities子模块库、Discrete子模块库。
①Continuous子模块库
连续系统最常用的有状态空间、传递函数、零极点模块:
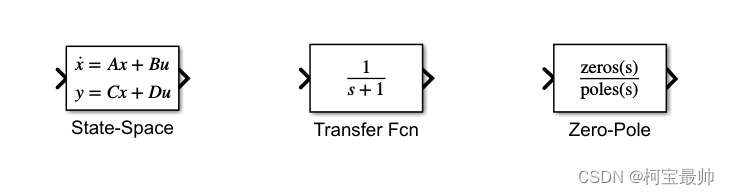
关键参数:系统矩阵A、输入矩阵B、输出矩阵C、反馈矩阵D;分子多项式num、分母多项式den;零点、极点、增益。
除了以上3个系统模型模块,控制器设计方面提供了单自由度PID控制器和二自由度PID控制器:
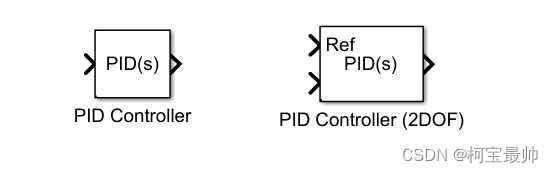
关键参数:控制器类型和形式、时域(连续or离散)、PID系数、滤波系数、初始条件、是否饱和及饱和程度;数据类型选项卡设置参数数据类型和最大最小值,默认为继承内部规则、无最值。
二自由度与单自由度的相似,但可以直接将系统的测量反馈信息与参考信号进行比较,还可指定P、I、D各项的权重,输出就是基于此权重。
②Discontinuities子模块库
提供模拟非线性环节的模块,间隙环节、死区环节、饱和环节:
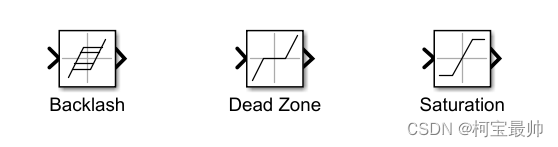
关键参数:死区宽度、初始输出;死区起始时刻、死区终止时刻;饱和上下限、是否过零检测。
③Discrete子模块库
提供离散系统模块,Continuous子模块库中介绍的模块名前加Discrete即成为离散系统模块。除此还有单位延迟、零阶保持器,可以比较下两者对信号作用的不同之处:
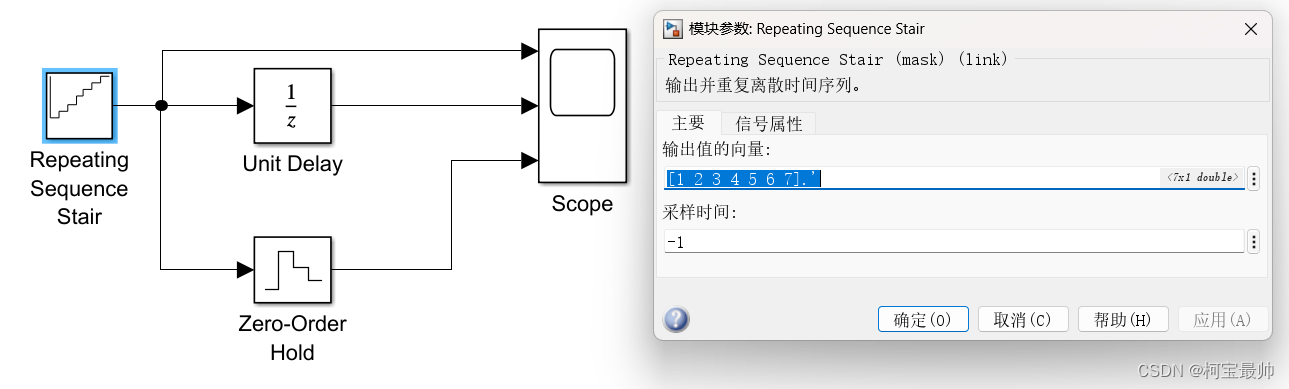
若把求解器设置如下,仿真结果为
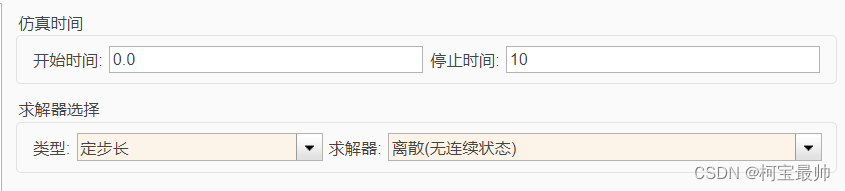
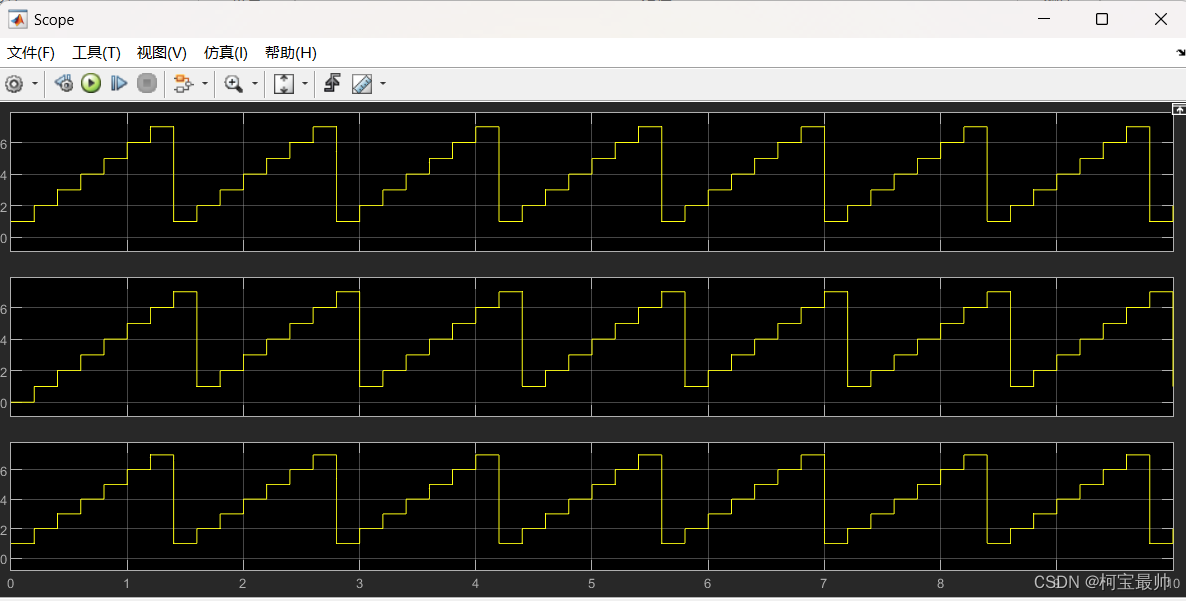
若求解器设置如下,仿真结果如下
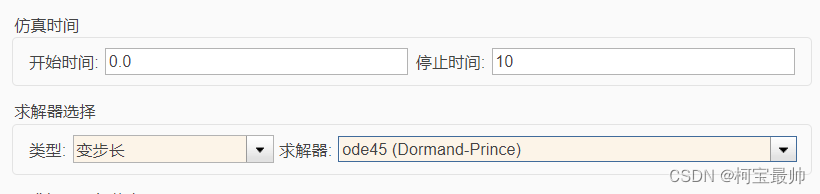
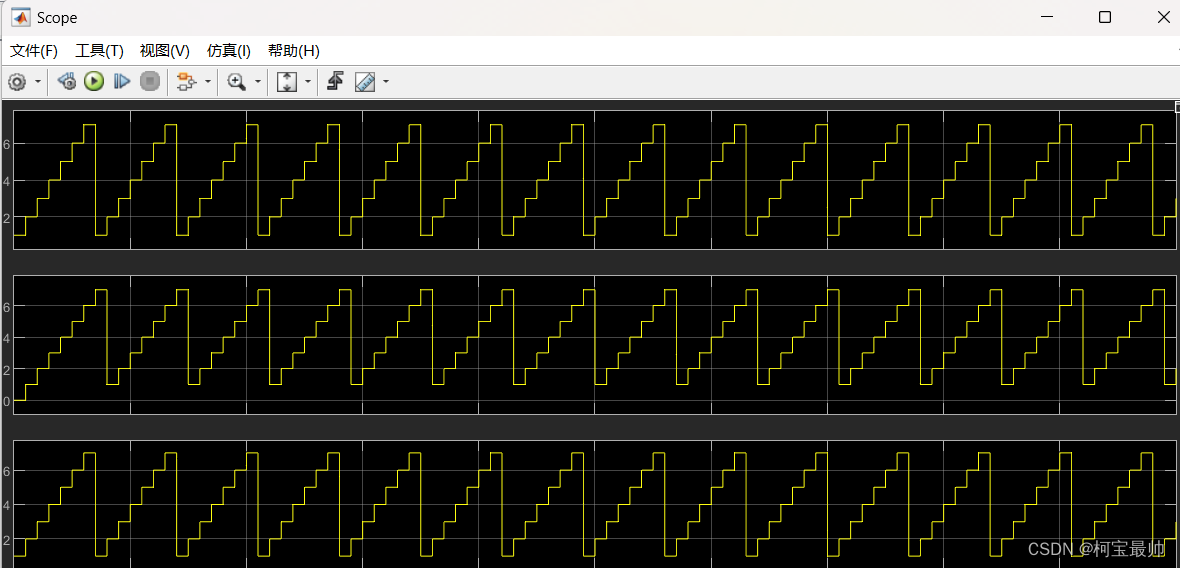
单位延迟unit delay在每一秒处保持输入值,但会延迟一个采样周期。
2、工具箱
控制系统工具箱中只有LTI System一个模块。LTI即线性时不变,既能模拟连续LTI模型,也能模拟离散LTI模型,传递函数形式、零极点形式和状态空间描述均可使用。
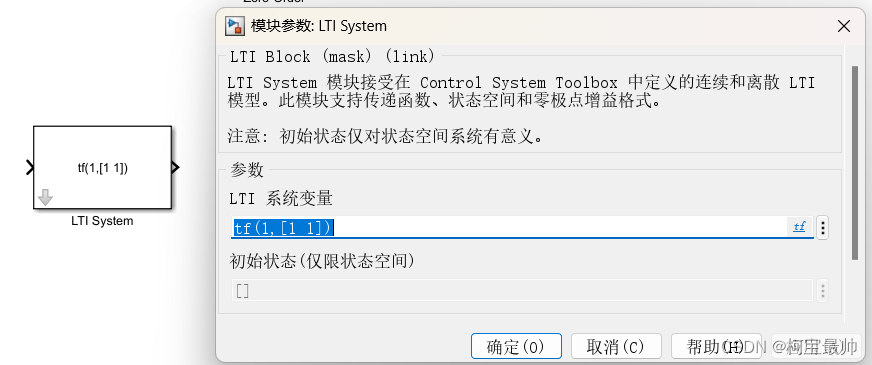
LTI系统变量就是设置连续or离散,传递函数形式、零极点形or状态空间描述。初始状态仅在状态空间描述时使用。
①可直接在模块参数框指定系统变量,如,设置tf([1 1],[1 5 1])。
②也可在Matlab编辑区定义,然后输入变量名
G1=tf([1 1],[1 5 1])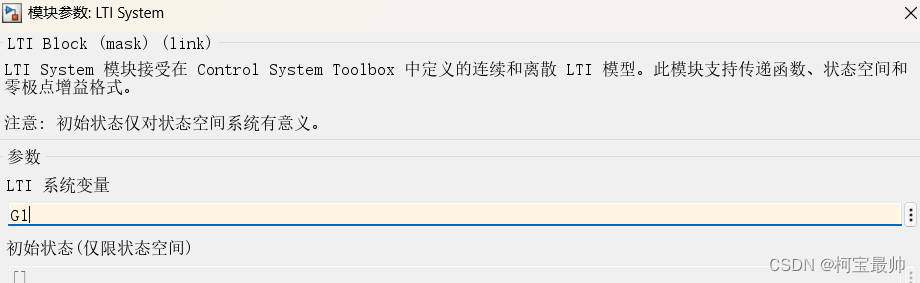
三、简单仿真实例
1、传递函数/零极点模型
阶跃响应曲线
这个省略,连接后输入信号设置为step,仿真后scope图像即为阶跃响应。
Bode图&Nyquist图&Nichols图(稳定性判别)
num=25*[1 1 7];
den=conv([1 25],[1 3 7]);
G=tf(num,den);
figure(1)
bode(G)
figure(2)
nyquist(G)
axis equal
figure(3)
nichols(G)
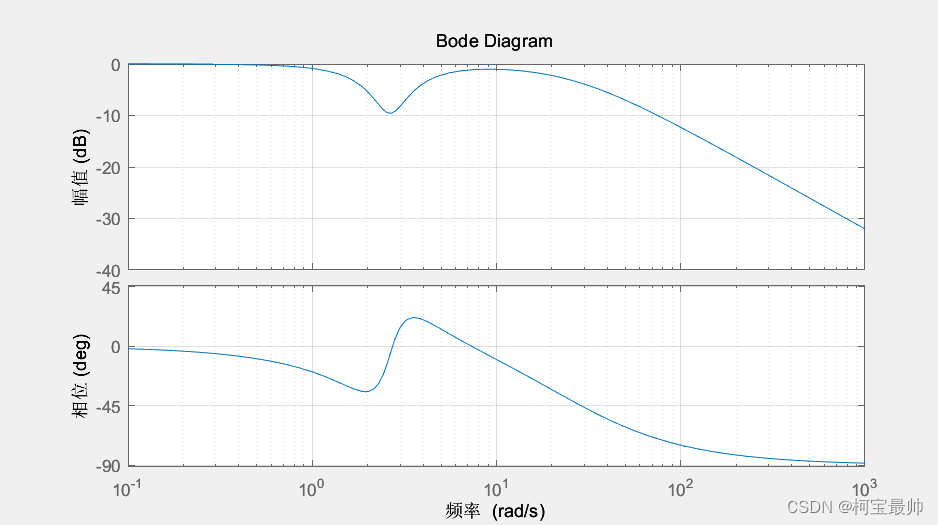
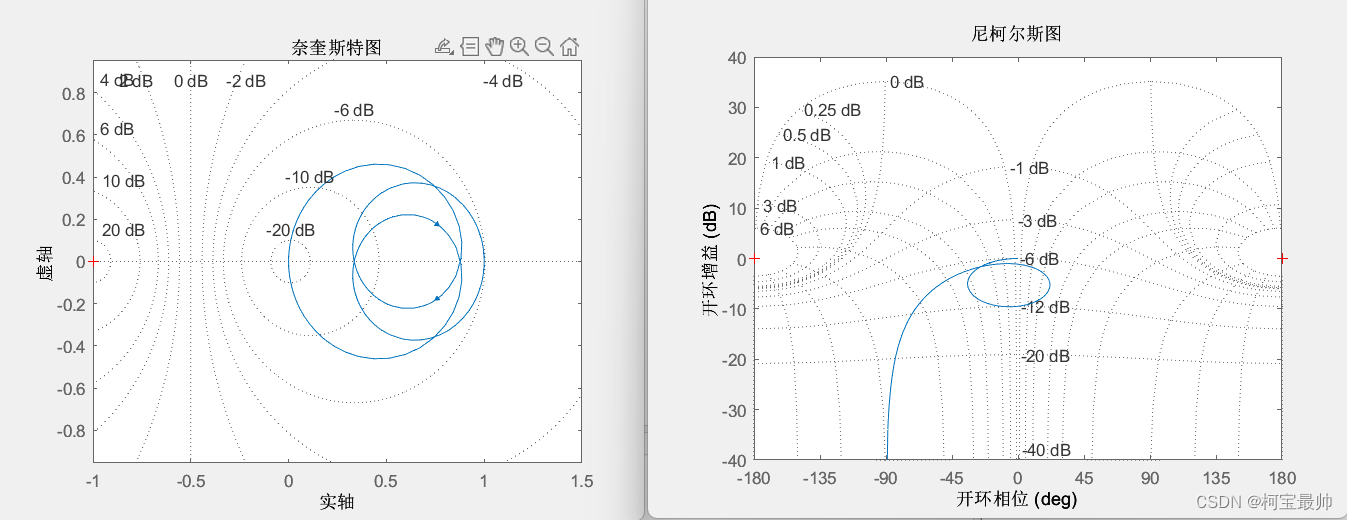
2、状态空间模型
一级倒立摆的状态空间模型:
这是一种不稳定、能控能观系统,设计一个二次型状态反馈调节器对其控制,并绘制阶跃响应曲线。首先应该判别稳定性、能控性、能观性,可选用二次型性能指标中的系数矩阵的值为:
稳定性判别
A=[0 0 1 0;0 0 0 1;0 -0.524 -3.129 0;0 -15.332 9.012 -0.562];
B=[0;0;81.23;-120.1];
C=[1 0 0 0;0 1 0 0];
D=0;
sys=ss(A,B,C,D); %状态空间模型
E=eig(A) %根据特征值判断稳定性
OB=obsv(A,C);%计算能控性矩阵的秩
N_B=rank(OB)
OC=ctrb(A,B);%计算能观性矩阵的秩
N_C=rank(OC)
Q=diag([1 0.01 0.01 0.1]);
R=45;
N=0;
[K,S,e]=lqr(sys,Q,R,N);%计算反馈矩阵K
sysT=ss(A-B*K,B,C,D);%加入控制器后的系统
step(sysT) %绘制加入控制器后的系统的阶跃响应曲线
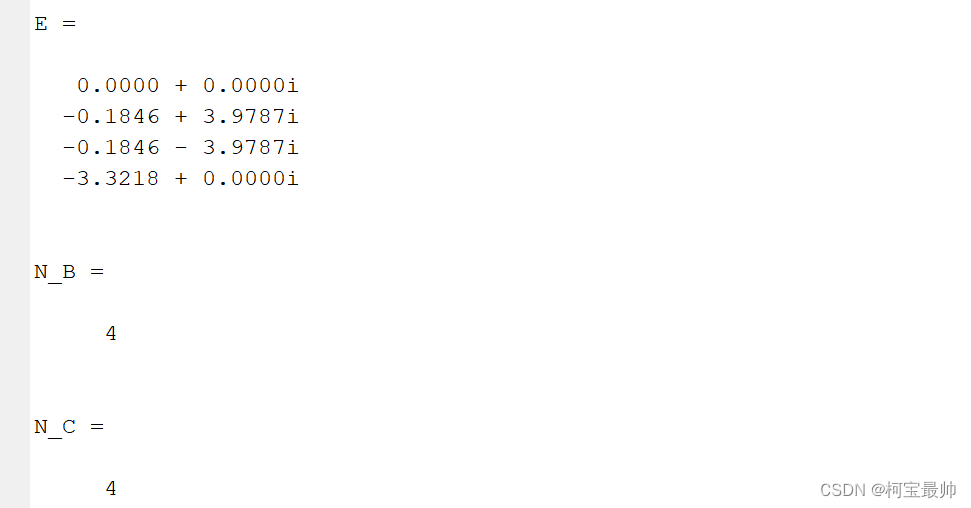
可看出原系统:不稳定、能控能观。
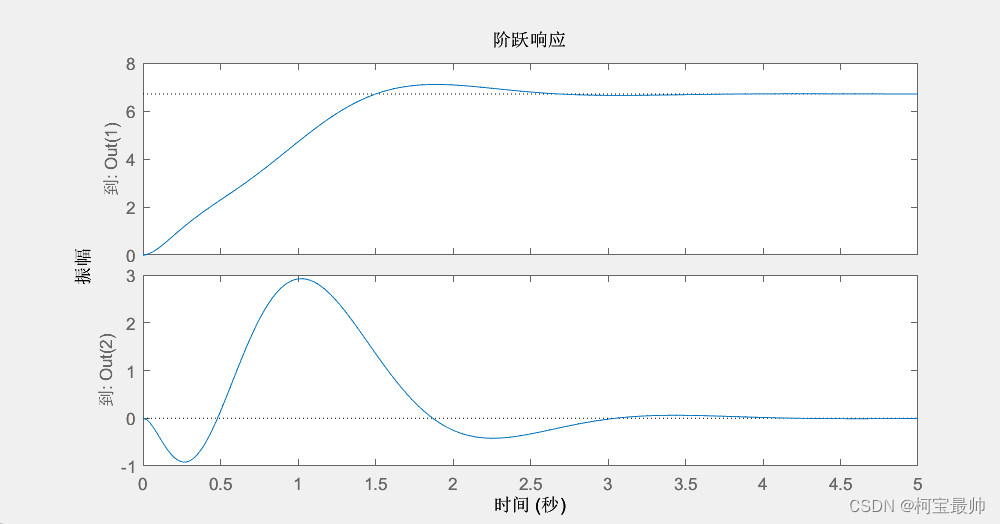
阶跃响应曲线
下面为加入反馈器后系统的阶跃响应,上面是位移曲线,下面为摆角曲线,最终都趋于稳定。
往期精彩
STM32专栏(付费9.9)![]() http://t.csdnimg.cn/E2F88
http://t.csdnimg.cn/E2F88
OpenCV-Python专栏(付费9.9)![]() http://t.csdnimg.cn/zK1jV
http://t.csdnimg.cn/zK1jV
AI底层逻辑专栏(付费9.9)![]() http://t.csdnimg.cn/zic0f
http://t.csdnimg.cn/zic0f
机器学习专栏(免费)![]() http://t.csdnimg.cn/FaXzAFreeRTOS专栏(免费)
http://t.csdnimg.cn/FaXzAFreeRTOS专栏(免费)![]() http://t.csdnimg.cn/SjIqU电机控制专栏(免费)
http://t.csdnimg.cn/SjIqU电机控制专栏(免费)![]() http://t.csdnimg.cn/FNWM7
http://t.csdnimg.cn/FNWM7


:字符串、列表、字典操作)



![[渗透教程]-022-内网穿透的高性能的反向代理应用](http://pic.xiahunao.cn/[渗透教程]-022-内网穿透的高性能的反向代理应用)









)


