随想录日记part14
t i m e : time: time: 2024.03.07
主要内容:今天的主要内容是二叉树的第三部分,主要涉及二叉树最大深度;二叉树最小深度;完全二叉树的节点个数。
- 104.二叉树的最大深度
- 111.二叉树的最小深度
- 222.完全二叉树的节点个数
Topic1二叉树的最大深度
题目: 给定一个二叉树 r o o t root root ,返回其最大深度。
二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
示例:

输入: r o o t = [ 3 , 9 , 20 , n u l l , n u l l , 15 , 7 ] root = [3,9,20,null,null,15,7] root=[3,9,20,null,null,15,7]
输出: 3 3 3
思路: 这道题目比较简答采用递归和迭代来实现:
下面给出两种的写法:
class Solution {public int maxDepth(TreeNode root) {// 递归法if (root == null)return 0;// 递归出口// 单层递归逻辑int left = maxDepth(root.left);int right = maxDepth(root.right);if (left >= right)return left + 1;elsereturn right + 1;}
}class Solution {public int maxDepth(TreeNode root) { 使用层序遍历进行迭代法if(root==null)return 0;Deque<TreeNode> queue = new LinkedList<>();int deep=0;queue.add(root);while(!queue.isEmpty()){deep++;//记录深度int te=queue.size();for(int i=0;i<te;i++){TreeNode tem=queue.poll();if(tem.left!=null)queue.add(tem.left);if(tem.right!=null)queue.add(tem.right);}}return deep;}
}
Topic2二叉树的最小深度
题目: 给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例: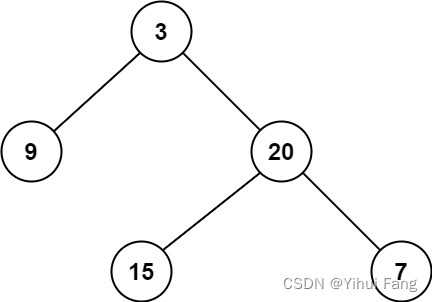
输入: r o o t = [ 3 , 9 , 20 , n u l l , n u l l , 15 , 7 ] root = [3,9,20,null,null,15,7] root=[3,9,20,null,null,15,7]
输出: 2 2 2
思路: 整个树的翻转主要有两种思路:
- 递归
- 迭代
- 递归法:写好递归是要有三个关键点注意的:
1.确定参数和返回值
int minDepth(TreeNode root);
2.确定中止条件
if (root == null) return 0;
3.确定单层递归逻辑,这里的递归逻辑得注意
int left = minDepth(root.left);int right = minDepth(root.right);//这里的单层循环处理注意if (root.left == null && root.right != null)return right + 1;if (root.left != null && root.right == null)return left + 1;if (left >= right)return right + 1;elsereturn left + 1;
完整的 j a v a java java 代码如下:
class Solution {public int minDepth(TreeNode root) {//递归法if (root == null)return 0;int left = minDepth(root.left);int right = minDepth(root.right);//这里的单层循环处理注意if (root.left == null && root.right != null)return right + 1;if (root.left != null && root.right == null)return left + 1;if (left >= right)return right + 1;elsereturn left + 1;}
}
- 迭代法:能够使用队列来实现:
如下面代码实现:
class Solution {public int minDepth(TreeNode root) {// 使用层序遍历实现迭代法if (root == null)return 0;Deque<TreeNode> queue = new LinkedList<>();int deep = 0;queue.add(root);while (!queue.isEmpty()) {deep++;// 记录深度int te = queue.size();for (int i = 0; i < te; i++) {TreeNode tem = queue.poll();if (tem.left != null)queue.add(tem.left);if (tem.right != null)queue.add(tem.right);if (tem.left == null && tem.right == null)//当前节点的左右节点都为空,其为叶子节点return deep;}}return deep;}
}
Topic3完全二叉树的节点个数
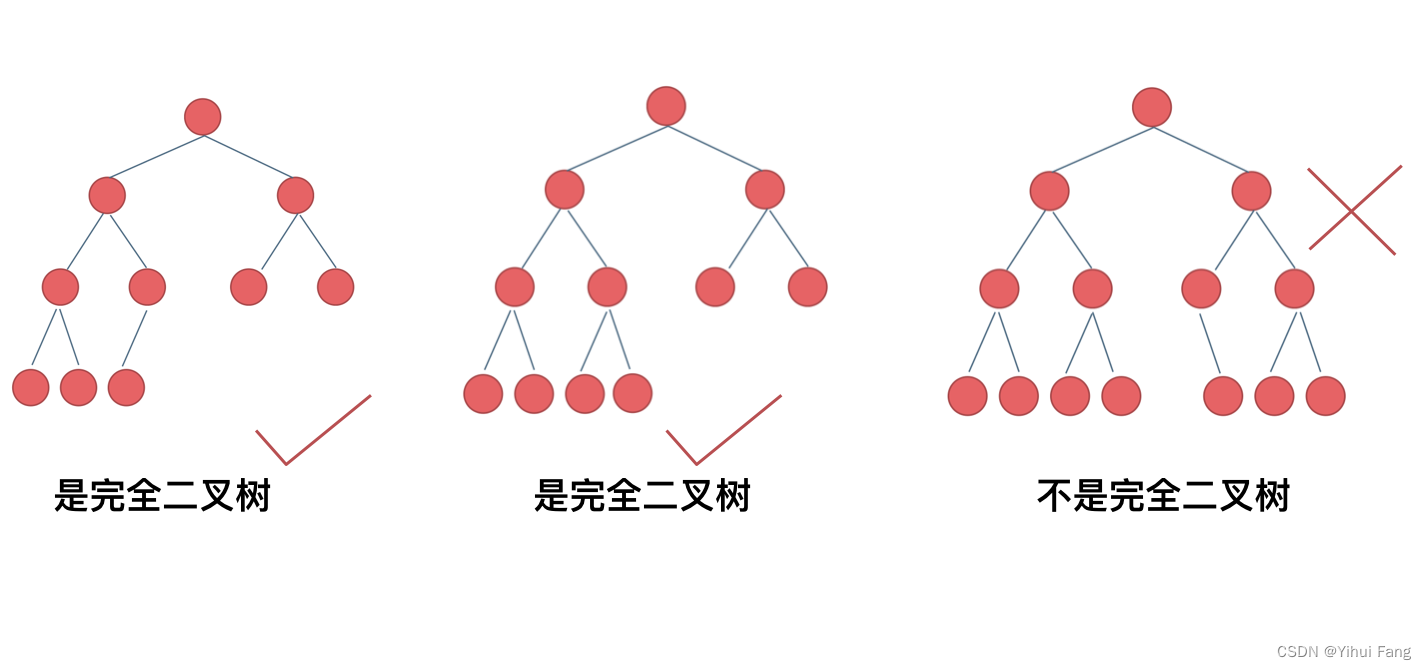
题目: 给你一棵 完全二叉树 的根节点 r o o t root root ,求出该树的节点个数。完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h h h 层,则该层包含 1 1 1 ~ 2 h 2^h 2h 个节点。
示例:
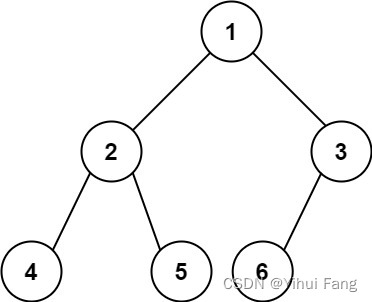
输入: r o o t = [ 1 , 2 , 3 , 4 , 5 , 6 ] root = [1,2,3,4,5,6] root=[1,2,3,4,5,6]
输出: 6 6 6
思路:
递归法:
class Solution {public int countNodes(TreeNode root) {//递归法if(root==null)return 0;int left=countNodes(root.left);int right=countNodes(root.right);return left+right+1;}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( l o g n ) O(logn) O(logn),算上了递归系统栈占用的空间
迭代法:
代码实现如下:
class Solution {public int countNodes(TreeNode root) {// 迭代法if (root == null)return 0;int count = 0;Deque<TreeNode> queue = new LinkedList<>();queue.add(root);while (!queue.isEmpty()) {count++;TreeNode tem = queue.poll();if (tem.left != null)queue.add(tem.left);if (tem.right != null)queue.add(tem.right);}return count;}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
-完全二叉树
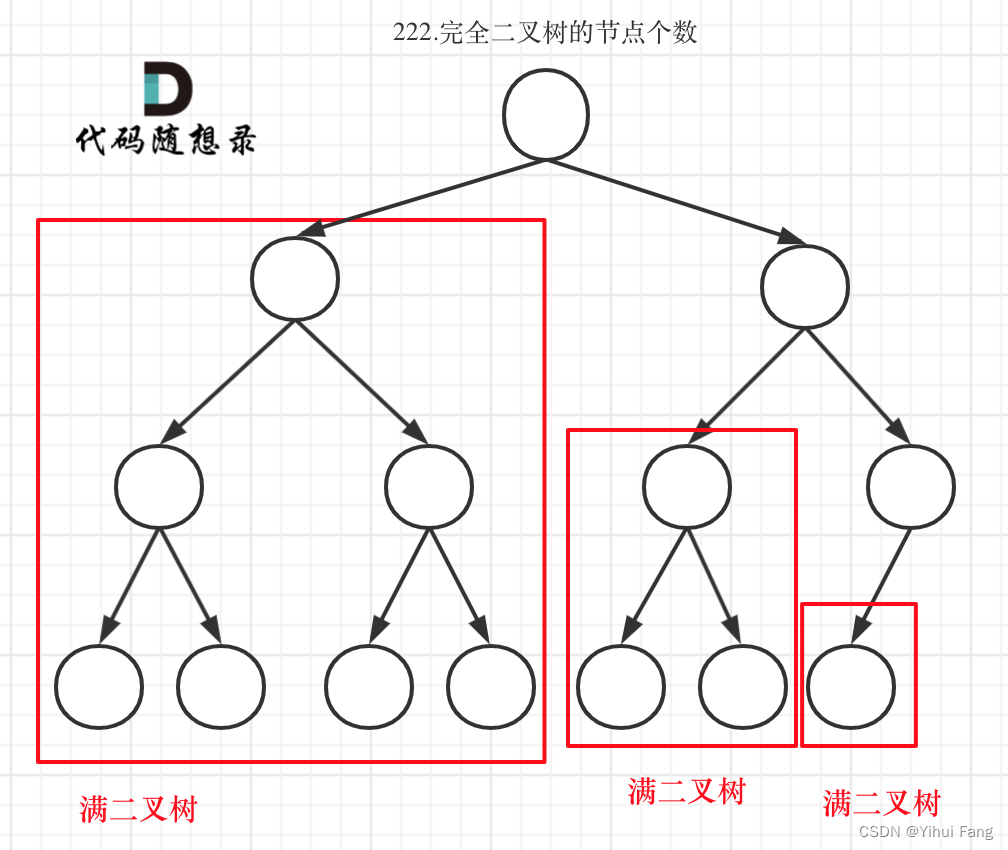
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2 树深度 − 1 2^{树深度} - 1 2树深度−1 来计算,注意这里根节点深度为 1 1 1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况 1 1 1 来计算。
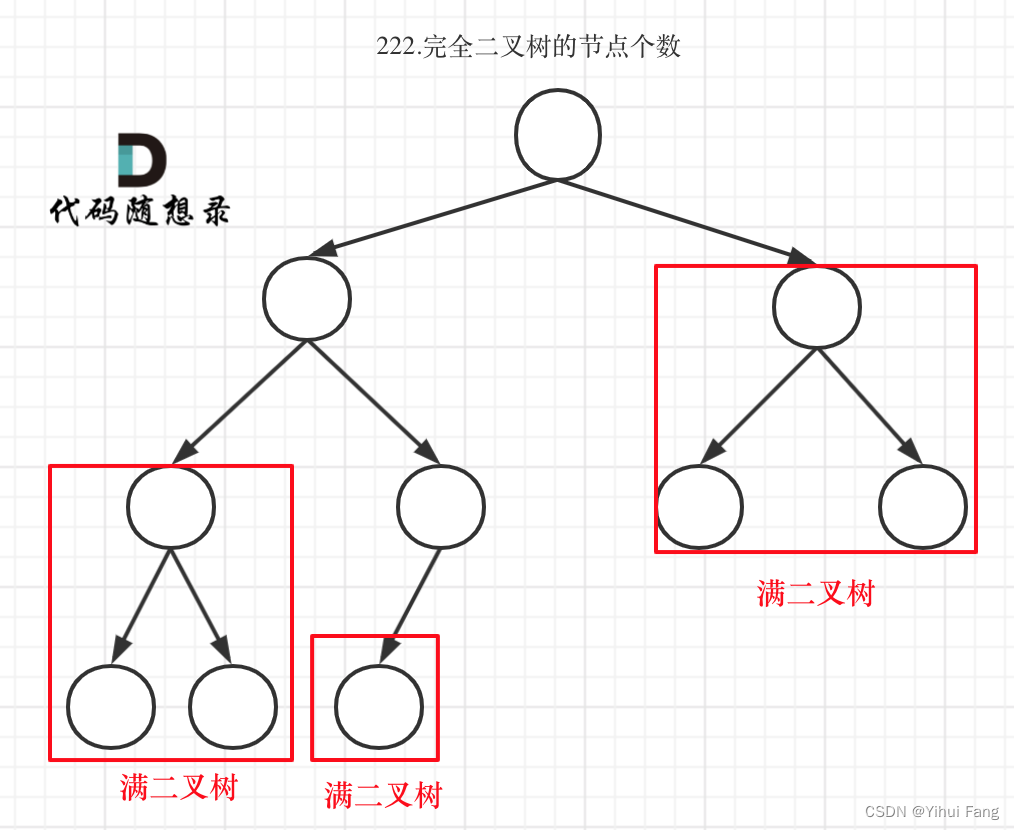
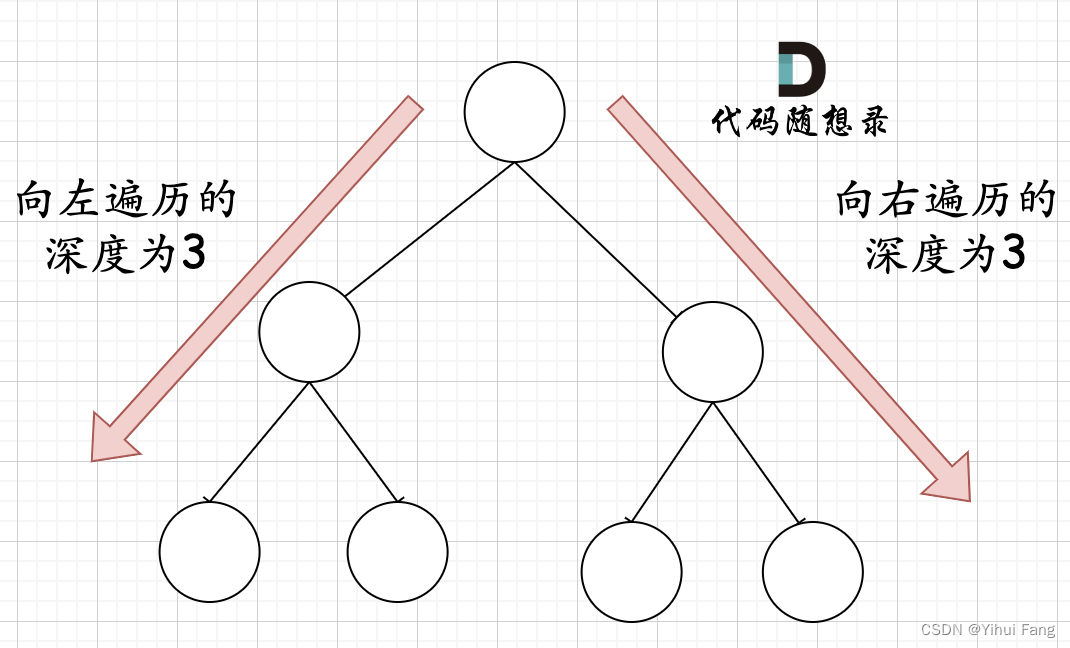
完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。
其完整的Java代码如下:
ass Solution {public int countNodes(TreeNode root) {// 利用完整二叉树的性质// 递归出口if (root == null)return 0;// 单层递归的逻辑TreeNode left = root.left;TreeNode right = root.right;int leftdepth = 0;int rightdepth = 0;while (left != null) {left = left.left;leftdepth++;}while (right != null) {right = right.right;rightdepth++;}if (leftdepth == rightdepth) {return (2 << leftdepth) - 1;}return 1 + countNodes(root.left) + countNodes(root.right);}
}
时间复杂度: O ( l o g n × l o g n ) O(log\ n × log\ n) O(log n×log n)
空间复杂度: O ( l o g n ) O(log\ n) O(log n)




)




-Causal Attention for Vision-Language Tasks(文献阅读))
)




)



