【数据结构】堆排序

大家好，我是苏貝，本篇博客带大家了解堆排序，如果你觉得我写的还不错的话，可以给我一个赞👍吗，感谢❤️

一. 堆的概念

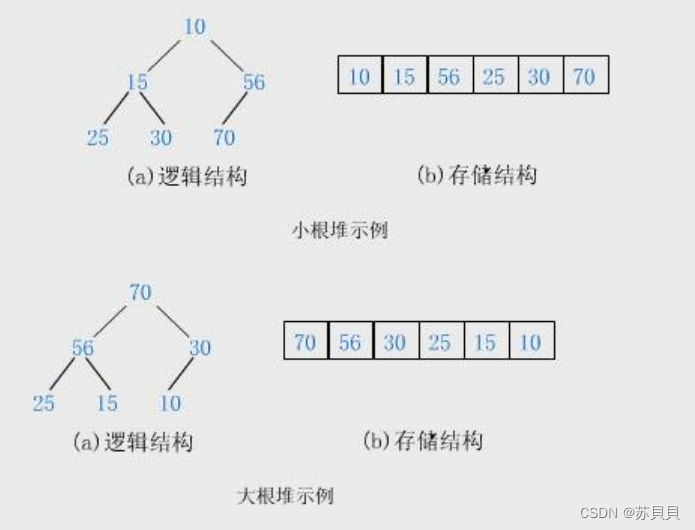
如果有一个关键码的集合K，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：任意一个双亲结点的值<=孩子节点的值（或任意一个双亲结点的值>=孩子节点的值），则称为小堆(或大堆)。堆排序即利用堆的思想来进行排序

在这里插入图片描述

二. 堆排序（以升序为例）

思路:

1.将待排序的数组构成一个大堆，此时堆顶元素就是最大的
2.将堆顶元素与最后一个元素交换，此时最后一个元素就是最大值
3.删除最后一个元素（实际上没有删除，只是不再和其它元素一起构成大堆），让其它元素再次构成大堆
4.重复第2、3步：将堆顶元素与最后一个元素（其实是倒数第二个）交换，此时它就是最大值（其实是次大值）……

1
为什么不用小堆？

因为小堆只能保证孩子节点的值>=双亲结点的值，不能保证兄弟节点也是按升序排列的，如：

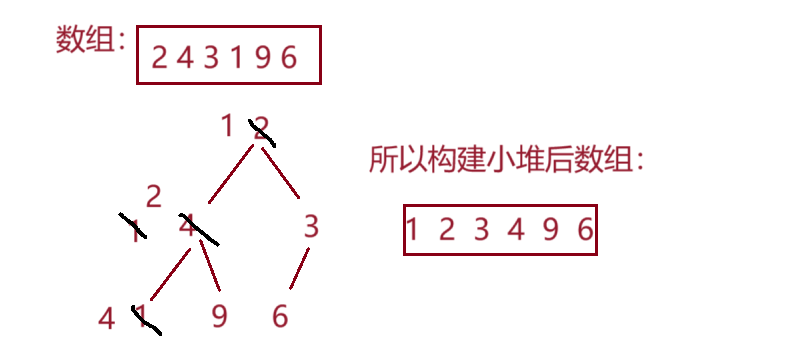
在这里插入图片描述
从上面我们可以看出，该数组最后并不是升序排列的，因此我们不能构建小堆

2
如何构建大堆？

【数据结构】实现堆
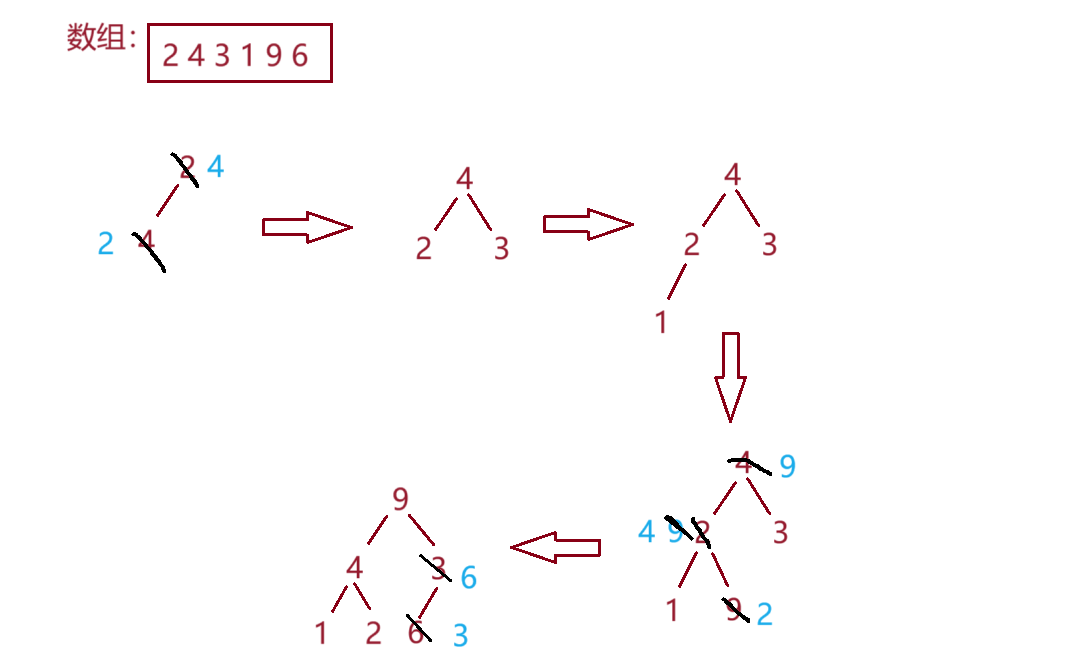
在上篇博客中，我们在实现堆时，在插入函数中用了向上调整的方法，在这里我们同样也可以采用向上调整的方法。插入第二个元素判断位置是否合适，如果该节点的值>双亲结点的值就向上调整，调整结束后，再插入并判断第三个元素是否合适……循环结束，大堆也就构建好了。

在这里插入图片描述

//void AdjustUp(int* a, int child)
//{
//	int parent = (child - 1) / 2;
//	while (child > 0)
//	{
//		if (a[child] > a[parent])
//		{
//			swap(&a[child], &a[parent]);
//			child = parent;
//			parent = (child - 1) / 2;
//		}
//		else
//		{
//			break;
//		}
//	}
//}
for (int i = 1; i < n; i++){AdjustUp(a, i);}

3
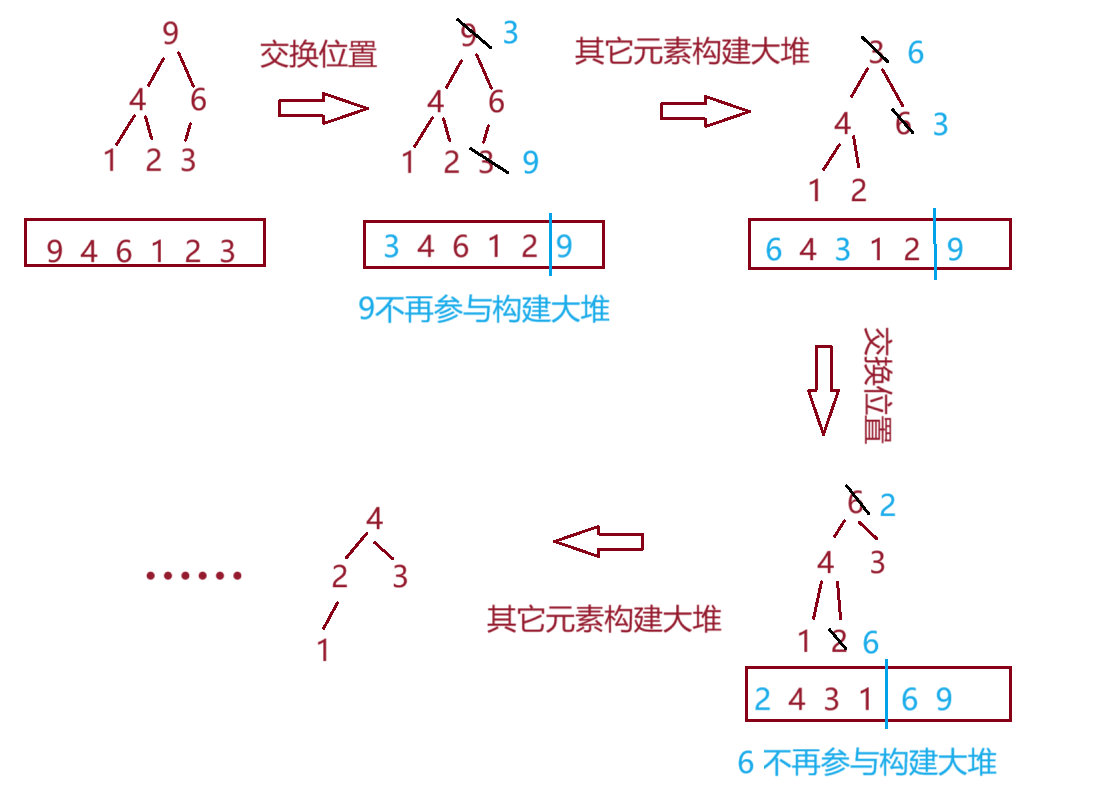
将堆顶元素与最后一个元素交换，然后删除最后一个元素（实际上没有删除）

在这里插入图片描述

//void AdjustDown(int* a, int size, int parent)
//{
//	int child = parent * 2 + 1;
//	while (child < size)
//	{
//		if (child + 1 < size && a[child + 1] > a[child])
//		{
//			child++;
//		}
//		if (a[parent] < a[child])
//		{
//			swap(&a[parent], &a[child]);
//			parent = child;
//			child = parent * 2 + 1;
//		}
//		else
//		{
//			break;
//		}
//	}
//}int end = n - 1;//n是数组的元素个数while (end > 0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}

4
建大堆的另一种思路

上面的2利用了插入思想，从第二个元素插入开始判断位置是否合适，不合适就向上调整，调整结束后，再插入并判断第三个元素是否合适……也就是说，在再次插入元素之前，所有的元素已经构成了大堆，插入元素后，再次调整直到为大堆。那如果我一次性插入所有的元素，此时双亲结点和孩子节点没有任何关系，是否还有方法能建成大堆呢？
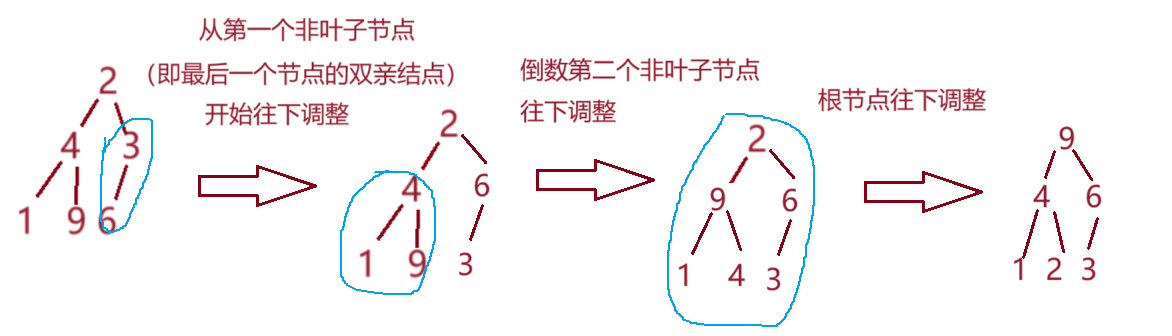
在这里插入图片描述
从第一个非叶子节点开始，不断向前移动，直到到根节点，每个节点都向下调整。i = (n - 1 - 1) / 2中，n-1是最后一个节点的索引，（孩子节点-1）/ 2==双亲结点的索引

for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}

5
向上和向下调整建堆的时间复杂度

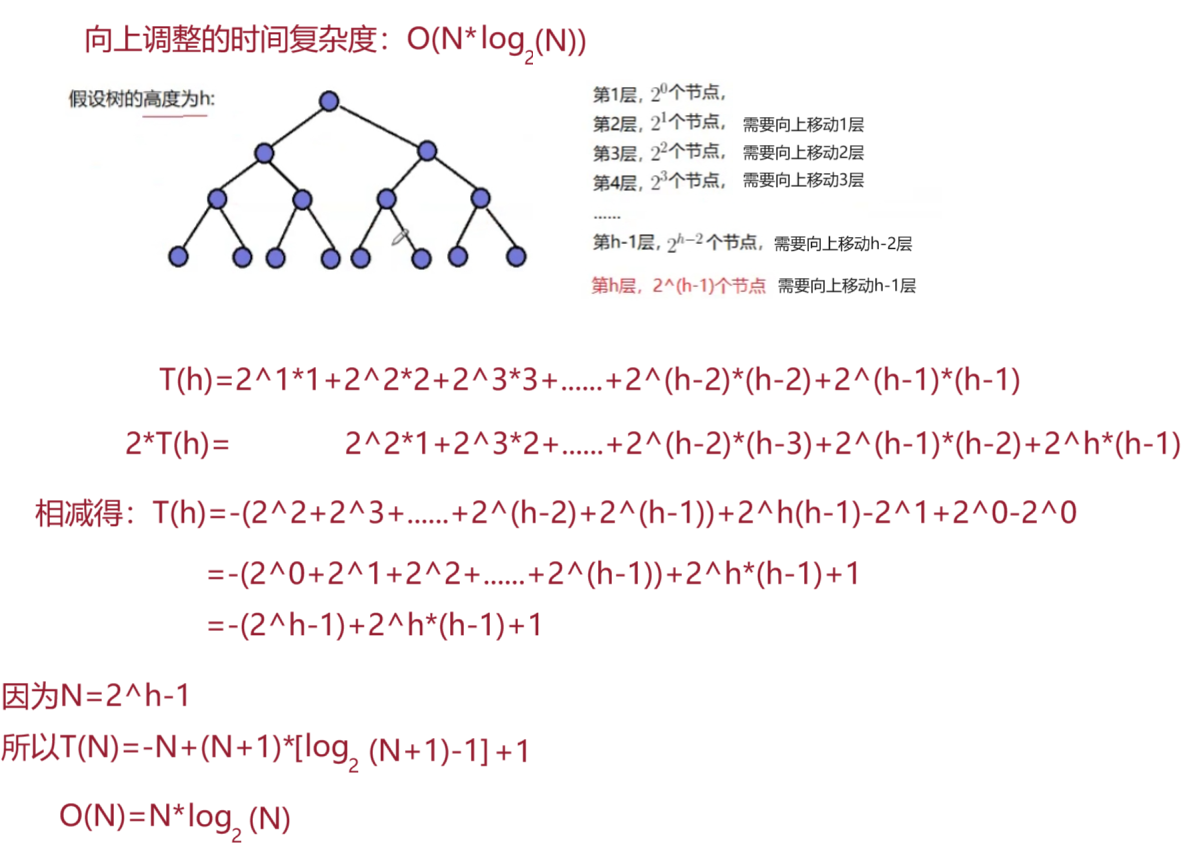
在这里插入图片描述

因为向上调整的时间复杂度为O(N*logN)，向下调整的时间复杂度为O(N)，所以向下调整的方法（上面的4）更好。

三. 代码

#include<stdio.h>
#include<time.h>
#include<stdlib.h>void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}}//升序
void HeapSort(int* a, int n)
{//1.建大堆/*for (int i = 1; i < n; i++){AdjustUp(a, i);}*/for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//2.排序int end = n - 1;while (end > 0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}int main()
{int a[] = { 2,4,3,1,9,6,7,8 };int n = sizeof(a) / sizeof(int);HeapSort(a, n);for (int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}