普通数组

1.最大子数组和

最大子数组和
前缀和pre + 动态规划
pre保留的是当前包含了当前遍历的最大的前缀和，如果之前的pre 对结果有增益效果，则 pre 保留并加上当前遍历, 如果pre 对结果无增益效果，需要舍弃，则 pre 直接更新为当前遍历数字；
每次比较 pre 和 maxAns的大小，将最大值置为maxAns，遍历结束返回结果。
时间复杂度：O(n)

class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();if (n == 1) return nums[0];int pre = 0, maxAns = nums[0];for (int i = 0; i < n; i++) {pre = max(pre + nums[i], nums[i]);maxAns = max(maxAns, pre);}return maxAns;}
};

普通数组

1.除自身以外数组的乘积

前缀和 * 后缀和
前缀和 = 前一个元素 * 前两个元素前缀和
用一个遍历来跟踪右边元素的乘积。并更新数组 answer[i]=answer[i]∗R。然后 R 更新为 R=R∗nums[i]，其中变量 R 表示的就是索引右侧数字的乘积。

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> ans(n, 1);int pre = 1, back = 1;for (int i = 1; i < n; i++) {ans[i] *= nums[i - 1] * ans[i - 1];}for (int i = n - 2; i >= 0; i--) {back *= nums[i + 1];ans[i] *= back;}return ans;}
};

矩阵

1.矩阵置零

矩阵置零
先用两个for记录出现0的行和列，再用两个for去标记出现0的所有行列元素
时间复杂度：O(mn)，其中 mmm 是矩阵的行数，nnn 是矩阵的列数。我们至多只需要遍历该矩阵两次。
空间复杂度：O(m+n)，其中 mmm 是矩阵的行数，nnn 是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();vector<int> row(n, 0), col(m, 0);for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (matrix[i][j] == 0)row[i] = col[j] = 1; }}for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (row[i] || col[j])matrix[i][j] = 0;}}}
};

2.螺旋矩阵

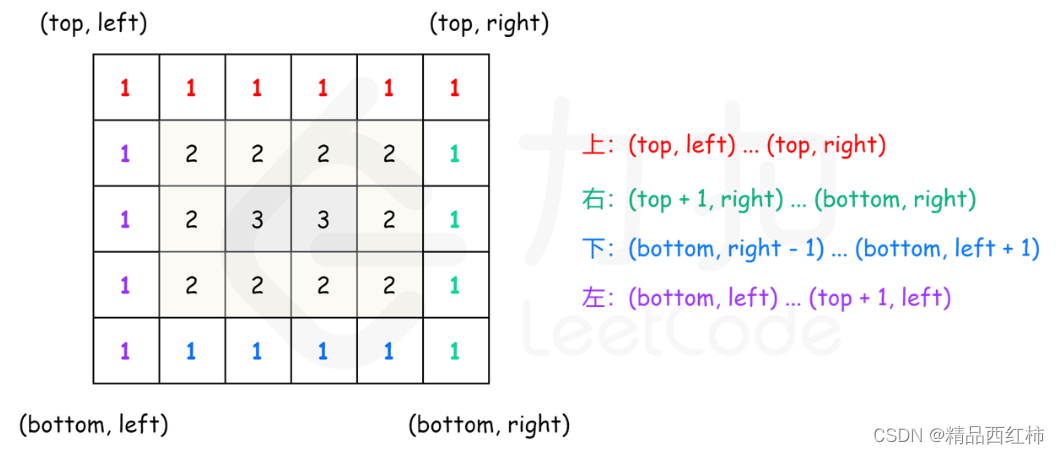
可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。

class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();vector<int> ans;int u = 0, d = n - 1;int l = 0, r = m - 1;while (true) {//左->右for (int i = l; i <= r; i++) {ans.push_back(matrix[u][i]);}u++;if (u > d) break;//上->下for (int i = u; i <= d; i++) {ans.push_back(matrix[i][r]);}r--;if(r < l) break;//右->左for (int i = r; i >= l; i--) {ans.push_back(matrix[d][i]);}d--;if(d < u) break;//下->上for (int i = d; i >= u; i--) {ans.push_back(matrix[i][l]);}l++;if(l > r) break;}return ans;}
};