论文地址:https://arxiv.org/pdf/2310.11453.pdf
相关博客
【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
【自然语言处理】BitNet b1.58:1bit LLM时代
【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer
【自然语言处理】【大模型】MPT模型结构源码解析(单机版)
【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版)
【自然语言处理】【大模型】BLOOM模型结构源码解析(单机版)
一、简介
语言模型的规模不断扩大,这对部署带来了巨大的挑战。本文设计了一种可扩展且稳定的1-bit Transformer架构来实现大语言模型,称为BitNet。具体来说,使用BitLinear作为标准nn的替代品。实验结果表明BitNet能够显著减少存储占用和能力消耗,并且与最先进的8-bit量化和FP16 Transformer能力相当。此外,BitNet也表现出了类似于全精度Transformer的scaling law,这也表明其有潜力在保持效率和性能的同时,能够更加有效的扩展至更大的语言模型。
二、BitNet

BitNet采用与Transformer相同的布局,但是采用BitLinear而不是标准的矩阵乘法,其他组件仍保持高精度。原因如下:(1) 残差连接和Layer Normalization的计算代价对于LLM可以忽略不计;(2) 随着模型增大,QKV变换的计算代价远小于投影;(3) 保留输入/输出嵌入层的精度,因为语言模型必须使用高精度来执行采样。
1. BitLinear
在二值化前将权重中心化为0均值来增加有限数值范围的容量,然后使用sign函数将权重二值化为+1或-1。二值化后使用缩放因子 β \beta β来降低实值权重和二值化权重之间的 l 2 l2 l2误差。因此,二值化权重 W ∈ R n × m W\in\mathcal{R}^{n\times m} W∈Rn×m可以形式化为:
W ~ = Sign ( W − α ) (1) \widetilde{W}=\text{Sign}(W-\alpha) \tag{1} \\ W =Sign(W−α)(1)
Sign ( W i j ) = { + 1 , if W i j > 0 − 1 , if W i j l e q 0 (2) \text{Sign}(W_{ij})=\begin{cases} +1,&&\text{if}\;W_{ij}>0 \\ -1,&&\text{if}\;W_{ij}leq 0 \\ \end{cases} \tag{2} \\ Sign(Wij)={+1,−1,ifWij>0ifWijleq0(2)
α = 1 n m ∑ i j W i j (3) \alpha=\frac{1}{nm}\sum_{ij}W_{ij} \tag{3} \\ α=nm1ij∑Wij(3)
接下来使用absmax将激活量化至b-bit,即乘以 Q b Q_b Qb再除以输入矩阵的最大绝对值,从而将激活缩放至 [ − Q b , Q b ] ( Q b = 2 b − 1 ) [-Q_b,Q_b](Q_b=2^{b-1}) [−Qb,Qb](Qb=2b−1):
x ~ = Quant ( x ) = Clip ( x × Q b γ , − Q b + ϵ , Q b − ϵ ) (4) \tilde{x}=\text{Quant}(x)=\text{Clip}(x\times\frac{Q_b}{\gamma},-Q_b+\epsilon,Q_b-\epsilon) \tag{4}\\ x~=Quant(x)=Clip(x×γQb,−Qb+ϵ,Qb−ϵ)(4)
Clip ( x , a , b ) = max ( a , min ( b , x ) ) , γ = ∥ x ∥ ∞ (5) \text{Clip}(x,a,b)=\max(a,\min(b,x)),\quad\gamma=\parallel x\parallel_\infty \tag{5} \\ Clip(x,a,b)=max(a,min(b,x)),γ=∥x∥∞(5)
其中 ϵ \epsilon ϵ是防止裁剪时溢出的小浮点数。
对于非线性函数之前的激活,通过减去输入中的最小值将其缩放至 [ 0 , Q b ] [0,Q_b] [0,Qb],从而使得所有值均为非负:
x ~ = Quant ( x ) = Clip ( ( x − η ) × Q b γ , ϵ , Q b − ϵ ) , η = min i , j x i j (6) \tilde{x}=\text{Quant}(x)=\text{Clip}((x-\eta)\times\frac{Q_b}{\gamma},\epsilon,Q_b-\epsilon),\quad\eta=\min_{i,j}x_{ij}\tag{6} \\ x~=Quant(x)=Clip((x−η)×γQb,ϵ,Qb−ϵ),η=i,jminxij(6)
本文中将激活量化至8-bit。此外,为了稳定性和效率,在训练期间按张量执行量化,而在推理时则按token执行量化。
基于上面的量化等式,矩阵乘法可以写作:
y = W ~ x ~ (7) y=\widetilde{W}\tilde{x}\tag{7} \\ y=W x~(7)
假设 W W W中的元素和 x x x是独立同分布的。那么,输出 y y y的方差可以估计为:
Var ( y ) = n Var ( w ~ x ~ ) = n E [ w ~ 2 ] E [ x ~ 2 ] = n β 2 E [ x ~ 2 ] ≈ E [ x ~ 2 ] \begin{align} \text{Var}(y)&=n\text{Var}(\tilde{w}\tilde{x}) \tag*{(8)} \\ &=nE[\tilde{w}^2]E[\tilde{x}^2] \tag*{(9)} \\ &=n\beta^2E[\tilde{x}^2]\approx E[\tilde{x}^2] \tag*{(10)} \end{align} \\ Var(y)=nVar(w~x~)=nE[w~2]E[x~2]=nβ2E[x~2]≈E[x~2](8)(9)(10)
对于全精度计算,若使用标准数据化方法,输出方差 Var ( y ) \text{Var}(y) Var(y)则为1,对于训练稳定性有益。为了在量化后保持方差,在激活量化前引入了LayerNorm函数。这样,输出 y y y的方差估计为 Var ( y ) ≈ E [ LN ( x ~ ) 2 ] = 1 \text{Var}(y)\approx E[\text{LN}(\tilde{x})^2]=1 Var(y)≈E[LN(x~)2]=1,其大小与全精度 Var ( y ) \text{Var}(y) Var(y)是相同量级。在标准的Transformer中,这种方式称为SubLN。利用SubLN和上述量化方法,得到BitLinear:
y = W ~ x ~ = W ~ Quant ( LN ( x ) ) × β γ Q b (11) y=\widetilde{W}\tilde{x}=\widetilde{W}\text{Quant}(\text{LN}(x))\times\frac{\beta\gamma}{Q_b}\tag{11} \\ y=W x~=W Quant(LN(x))×Qbβγ(11)
LN ( x ) = x − E ( x ) Var ( x ) + ϵ , β = 1 n m ∥ W ∥ 1 (12) \text{LN}(x)=\frac{x-E(x)}{\sqrt{\text{Var}(x)+\epsilon}},\quad\beta=\frac{1}{nm}\parallel W\parallel_1 \tag{12} \\ LN(x)=Var(x)+ϵx−E(x),β=nm1∥W∥1(12)
在SubLN操作之后,使用absmax函数对激活进行量化。然后1-bit权重和量化后的激活之间执行矩阵乘法。输出的激活使用 { β , γ } \{\beta,\gamma\} {β,γ}进行重新缩放,从而反量化至原始精度。
基于分组量化和规范化的模型并行。训练大语言模型的一项重要技术是模型并行,其在多个设备上划分矩阵乘法。现有模型并行方法的先决条件是张量在划分维度上是独立的。然而,所有参数 α \alpha α、 β \beta β、 γ \gamma γ和 η \eta η是从整个张量计算出来的,打破了独立性条件。为此,本文提出了一种简单且高效的模型并行方案。将权重和激活分为多个组,然后独立地估计每个组的参数。通过这种方式,可以在不需要额外通信的情况下本地计算这些参数。这种方法称为分组量化(Group Quantization),形式化为:
对于权重矩阵 W ∈ R n × m W\in\mathcal{R}^{n\times m} W∈Rn×m,将其沿着划分维度分为 G G G组,每个组的尺寸为 n G × m \frac{n}{G}\times m Gn×m。我们独立的估计每个组的参数:
α g = G n m ∑ i j W i j ( g ) , β g = G n m ∥ W ( g ) ∥ 1 (13) \alpha_g=\frac{G}{nm}\sum_{ij}W_{ij}^{(g)},\quad\beta_g=\frac{G}{nm}\parallel W^{(g)}\parallel_1 \tag{13} \\ αg=nmGij∑Wij(g),βg=nmG∥W(g)∥1(13)
其中 W ( g ) W^{(g)} W(g)是第 g g g个组的权重矩阵。类似地,对于激活,我们能将输入矩阵 x ∈ R n × m x\in\mathcal{R}^{n\times m} x∈Rn×m划分为 G G G组,每个组计算参数
γ g = ∥ x ( g ) ∥ ∞ , η g = min i j x i j ( g ) (14) \gamma_g=\parallel x^{(g)}\parallel_\infty,\quad\eta_g=\min_{ij}x_{ij}^{(g)}\tag{14} \\ γg=∥x(g)∥∞,ηg=ijminxij(g)(14)
对于LN,应用分组规范化(Group Normalization)技术来计算均值和方差:
LN ( x ( g ) ) = x ( g ) − E ( x ( g ) ) Var ( x ( g ) ) + ϵ (15) \text{LN}(x^{(g)})=\frac{x^{(g)}-E(x^{(g)})}{\sqrt{\text{Var}(x^{(g)})+\epsilon}} \tag{15} \\ LN(x(g))=Var(x(g))+ϵx(g)−E(x(g))(15)
通过分组量化和归一化能有效地实现模型并行,且不需要额外的通信。
2. 模型训练
直通估计器(Straight-through estimator, STE)。为了能够训练1-bit模型利用STE来在反向传播过程中近似梯度。该方法在反向传播过程中会绕开Sign或者Clip这样的不可微函数。因此,STE允许梯度在网络中流动而不受这些不可微函数的影响,使得训练量化模型成为可能。
混合精度训练。虽然权重和激活被量化为低精度,但是梯度和优化器状态仍然是按高精度存储,从而确保训练稳定性和准确率。遵循先前的工作,我们为可学习参数保持高精度格式的潜在权重,以累计参数更新。潜在权重在前向传播过程中被动态二值化,但是不会用在推理过程中。
大学习率。1-bit权重优化的挑战是小的更新量可能不会对权重有任何影响。在训练的开头,这个问题将更加的严重,因此期望模型尽快收敛。为了解决这个问题,探索了各种方法。最终,提高学习率是加速优化最简单且最好的方法。实验表明,大学习率能够使得BitNet很好的收敛,而FP16 Transformer使用大学习率会导致发散。
3. 计算效率
矩阵乘法是大语言模型计算的主要成本,因此这里也仅关注矩阵乘法的计算。
算术操作的能量。不同的算术操作的能量消耗估计如下:
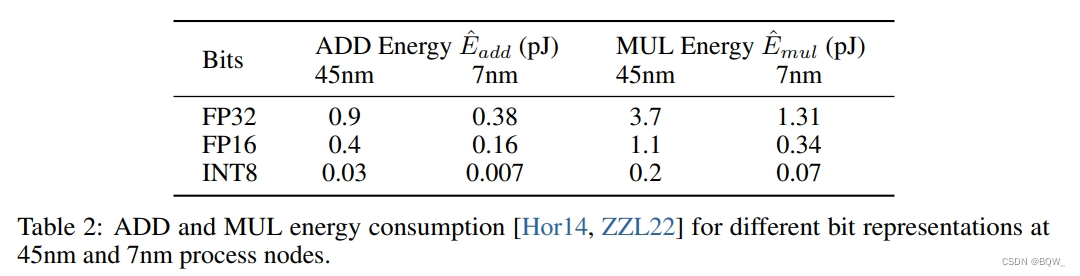
在标准Transformer中,若维度为 m × n m\times n m×n和 n × p n\times p n×p矩阵乘法能量消耗为
E a d d = m × ( n − 1 ) × p × E ^ a d d (16) E_{add}=m\times(n-1)\times p\times\hat{E}_{add} \tag{16} \\ Eadd=m×(n−1)×p×E^add(16)
E m u l = m × n × p × E ^ m u l (17) E_{mul}=m\times n\times p\times\hat{E}_{mul}\tag{17} \\ Emul=m×n×p×E^mul(17)
对于BitNet,由于权重是1-bit,因此矩阵乘法的能量消耗是由加法运算决定的。乘法运行仅应用于因子 β \beta β和 γ Q b \frac{\gamma}{Q_b} Qbγ缩放输出,因此乘法的能量消耗可以计算为:
E m u l = ( m × p + m × n ) × E ^ m u l (18) E_{mul}=(m\times p+m\times n)\times\hat{E}_{mul}\tag{18} \\ Emul=(m×p+m×n)×E^mul(18)
其明显小于Transformer。
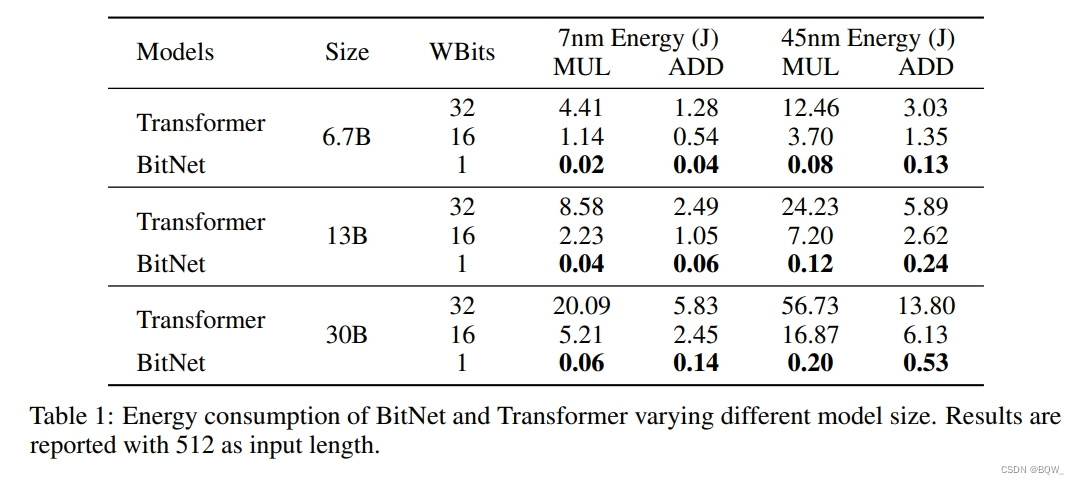
W1A8 BitNet相较于全精度(32-32)和半精度(16-16)的结果如上表1所示。可以看到,BitNet能够显著的节约能源。
三、与FP16 Transformer的比较
1. 设置
训练了一系列自回归BitNet模型,尺寸从125M至30B。这些模型是在英文语料上训练,包含Pile、Common Crawl 、RealNews和CC-Stories数据集。使用Sentencepiece tokenizer来预处理数据,词表尺寸为16K。除了BitNet,也用相同的数据集训练了Transformer baselines用于公平比较。
2. Inference-Optimal Scaling Law
标准Transformer自然语言模型已经被证明可以预测缩放的结果,损失值的大小由训练所使用的计算量决定。这使得能够确定计算预算的最佳分配,并从较小的模型中预测大型语言模型的性能。
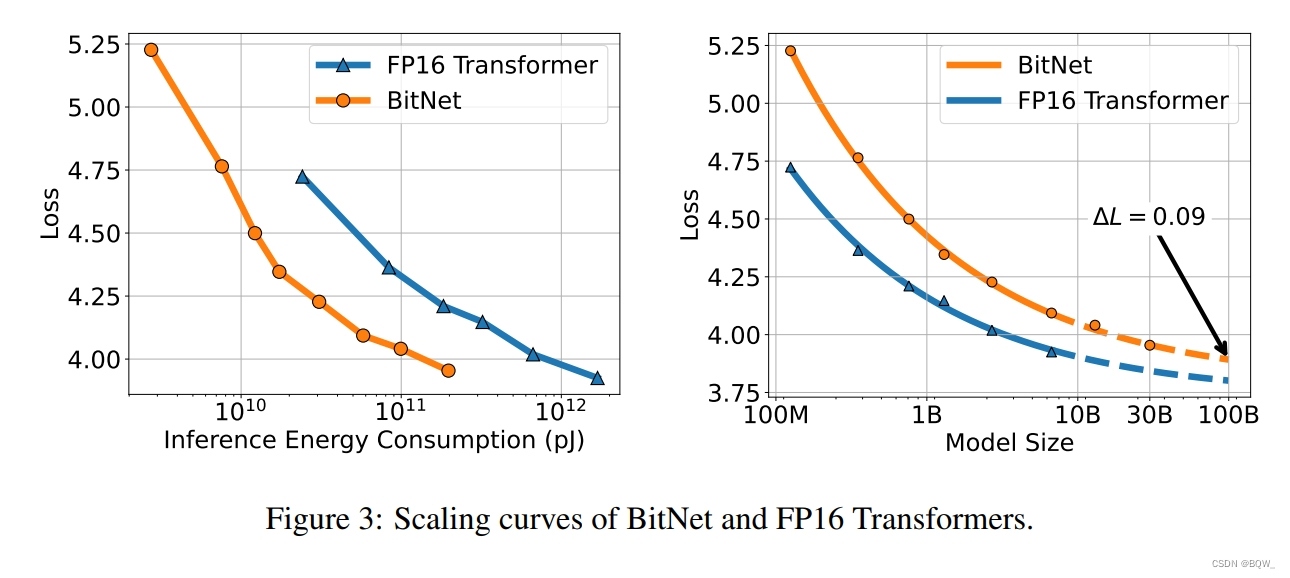
为了研究二值化Transformer的scaling law,绘制了BitNet和FP16 Transformer的scaling curve。上图3展示了BitNet的loss scaling,类似于FP16 Transformer,遵循幂律。这里用一个不可约损失项来拟合scaling law:
L ( N ) = a N b + c (19) L(N)=aN^b+c\tag{19} \\ L(N)=aNb+c(19)
为了评估scaling law是否能够准确预测loss,从125M至6.7B的模型来拟合幂律中的参数,并使用该定律来预测13B和30B的损失。结果表明,拟合后的scaling law能够准确的预测BitNet的损失函数。此外,随着模型尺寸的增加,BitNet和FP16 Transformer之间的差距越来越小。
上面的scaling law并没有正确地建模损失值和实际计算之间的关系。先前的工作通过计算FLOPs来估计计算量,但是其不适用于由整数计算主导的1-bit模型。此外,其主要是用于衡量训练的计算量,而不是推理。为了更好地理解神经语言模型的scaling效率,这里引入了Inference-Optimal Scaling Law。这主要是关注推理的成本,因此其会随着模型的使用而增加,但训练成本只有一次。上图3展示了7nm处理器相对于推理能力成本的scaling curve,其表明BitNet有更高的scaling效率。在给定固定计算预算的情况下,BitNet实现了更好的loss。此外,推理成本要小得多,可以获得与FP16模型相同的性能。
3. 下游任务结果
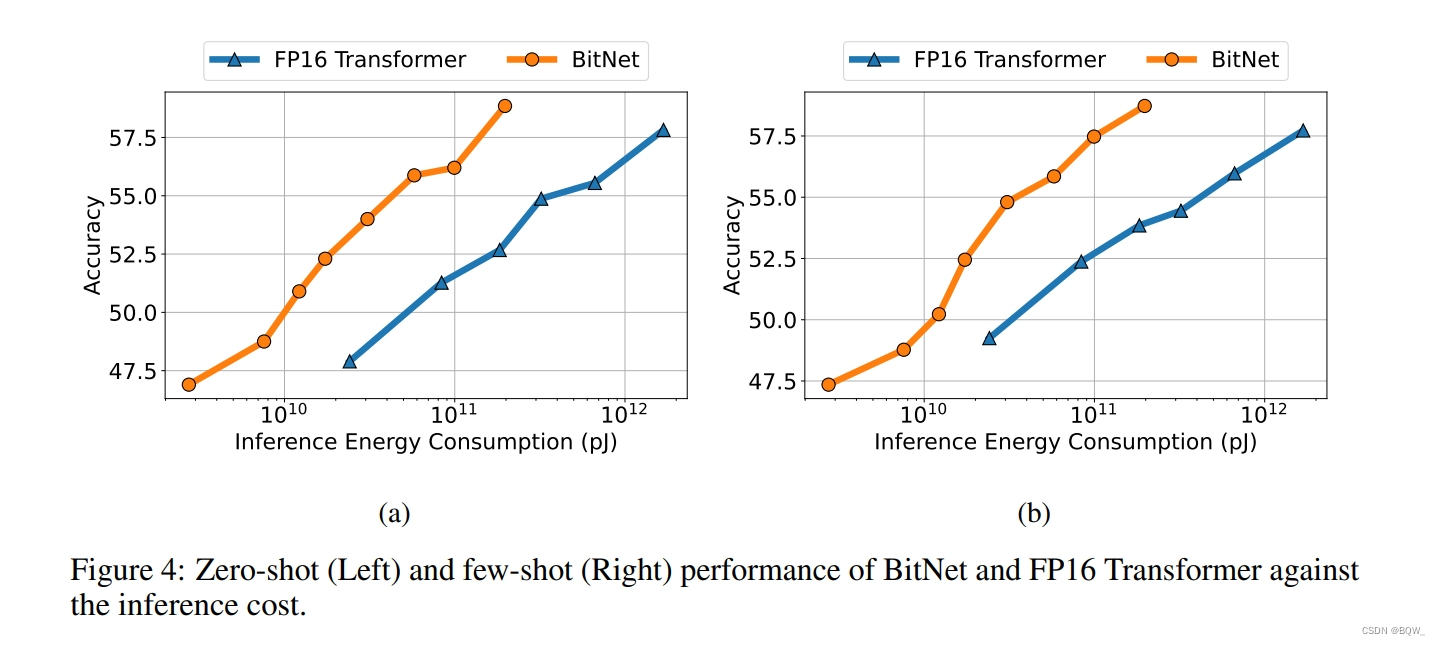
除了loss以外,还关注BitNet下游任务的能力。与loss相比,由于神经语言模型的涌现能力更难以预测。为了能够以可解释的度量来评估能力,在下游任务上测试了0-shot和4-shot的结果。上图4展示了不同规模的BitNet和FP16 Transformer的平均结果。与loss scaling curve类似,下游任务的性能可以随着计算预算的增加而增加。
4. 稳定性测试
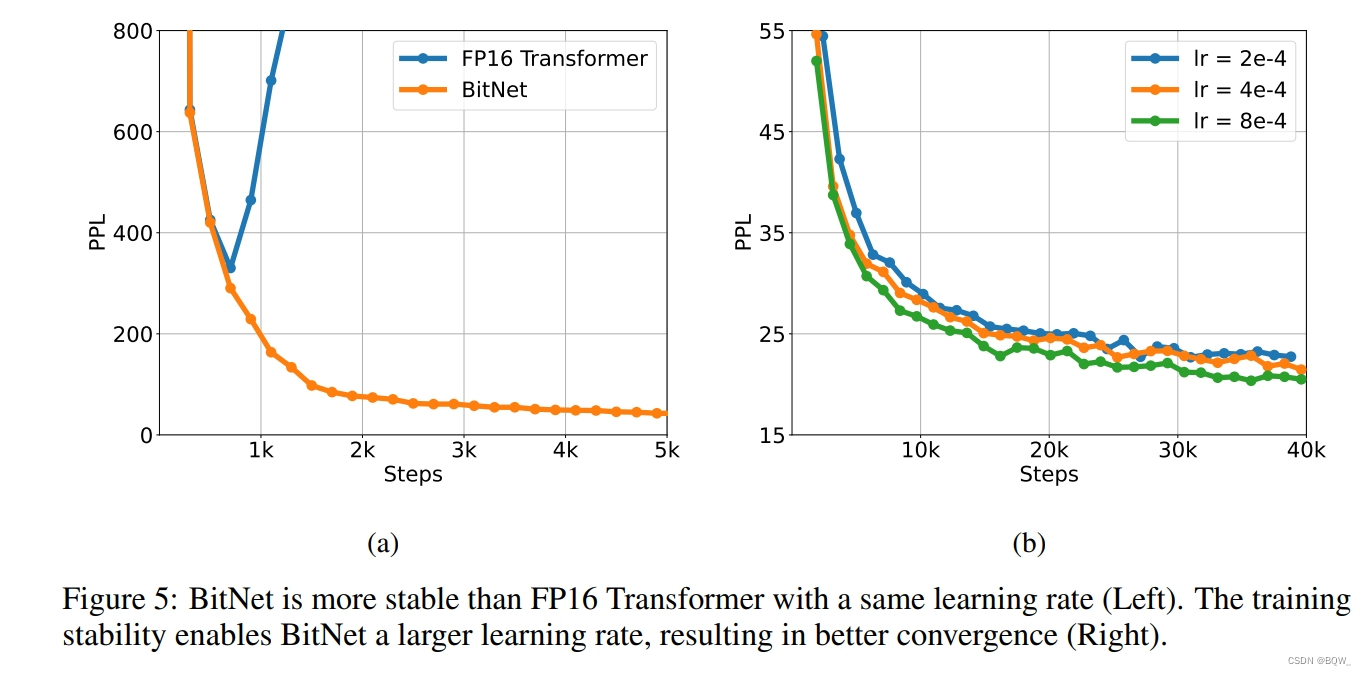
训练低精度Transformer的主要挑战是稳定性。因此,通过训练一系列具有不同峰值学习率的模型,对BitNet和FP16 Transformer进行了稳定性测试。上图5a展示了稳定性测试结果,表明BitNet可以以较大的学习率收敛,而FP16 Transformer则不能。上图5b展示了BitNet可以从增加的学习率中受益,实现PPL更好的收敛。
四、与Post-training量化的比较
1. 设置
这里将BitNet与最先进的量化方法进行了比较,包含Absmax、SmoothQuant、GPTQ和QulP。这些方法在FP16 Transformer模型上的post-training量化,其遵循与BitNet相同的训练设置和数据。其中,Absmax和SmoothQuant对权重和激活进行量化,而GPTQ和QulP只能降低权重的精度。应用这些方法在各种量化级别。对于weight-only量化,用W4A16和W2A16进行实验。对于权重和激活同时量化,将FP16 Transformer量化为W8A8、W4A4和W1A8。BitNet则使用二值权重和8-bit激活,其bits数小于等于baseline。
2. 结果
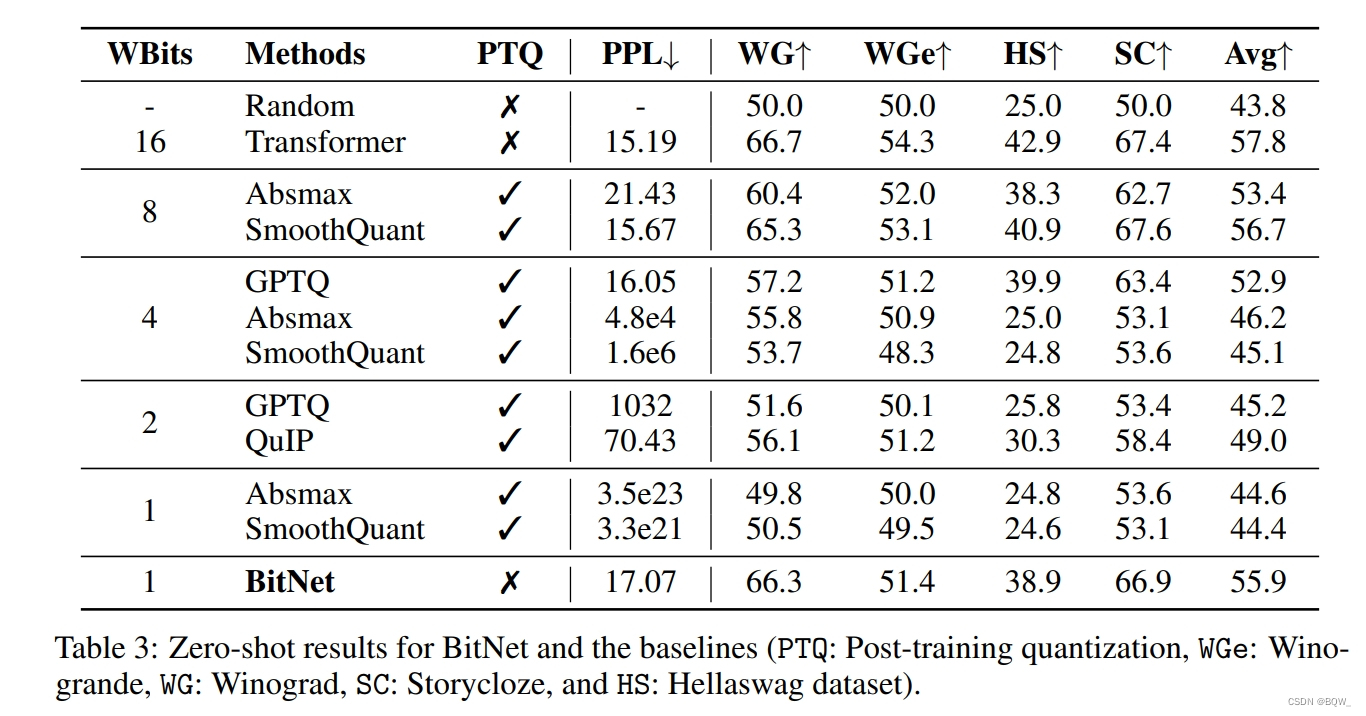
上面3是BitNet和各种baseline在四个基准数据集上zero-shot性能的详细分析。为了进行公平的比较,所有模型的大小均为6.7B。
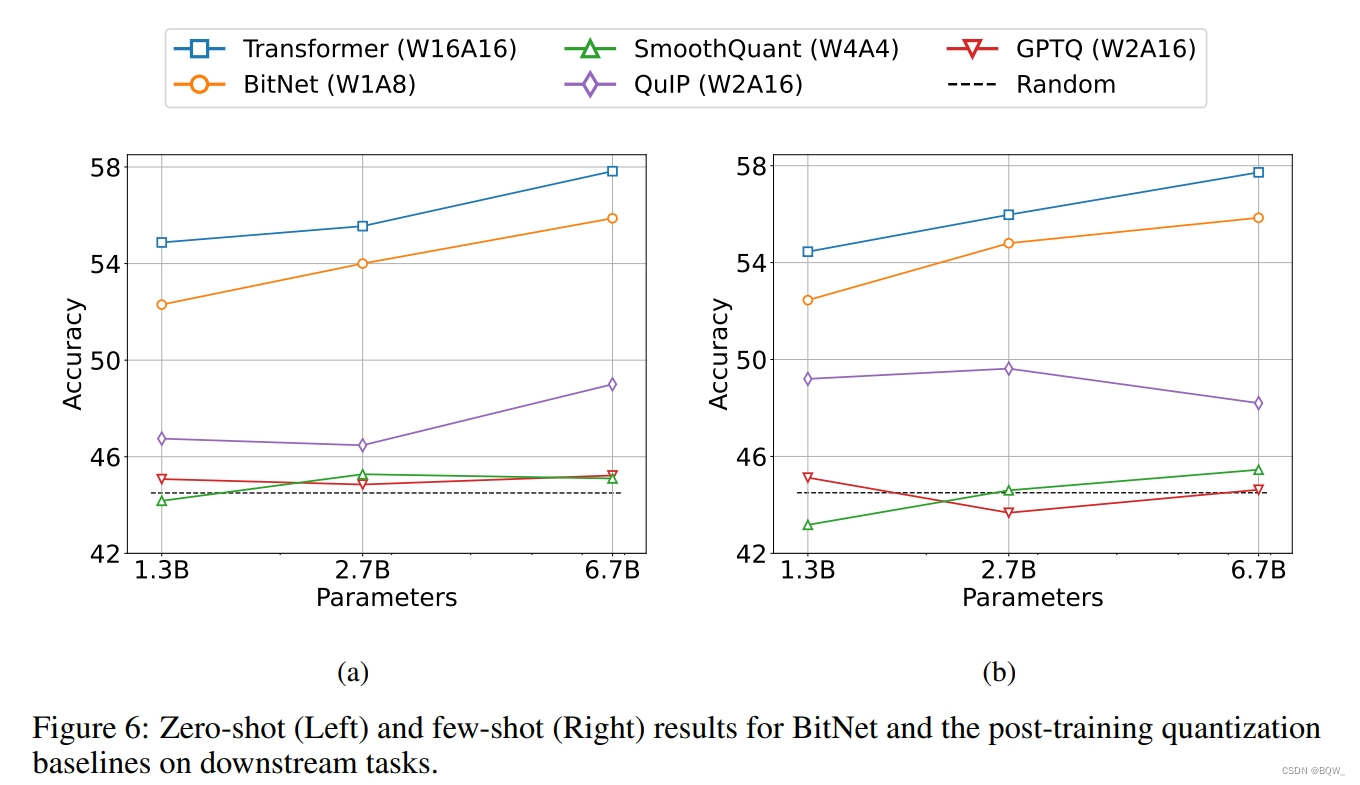
BitNet的zero-shot与8-bit模型相当,但是推理成本要低得多。对于4-bit模型,weight-only量化方法优于weight-and-activation量化方法,主要是因为激活更难量化。BitNet作为1-bit模型,显著优于各种量化方法。






?)






--基于GAN网络实现图像超分辨率重建)

)



