线性DP：

        所谓线性DP，是指递推方程有一种明显的线性关系存在。

        在状态规划中，状态可以是一维的，二维的，多维的。例如，在背包问题中，就是一个二维的状态，在求解状态的时候，是一个线性推进的过程。 

DP分析：

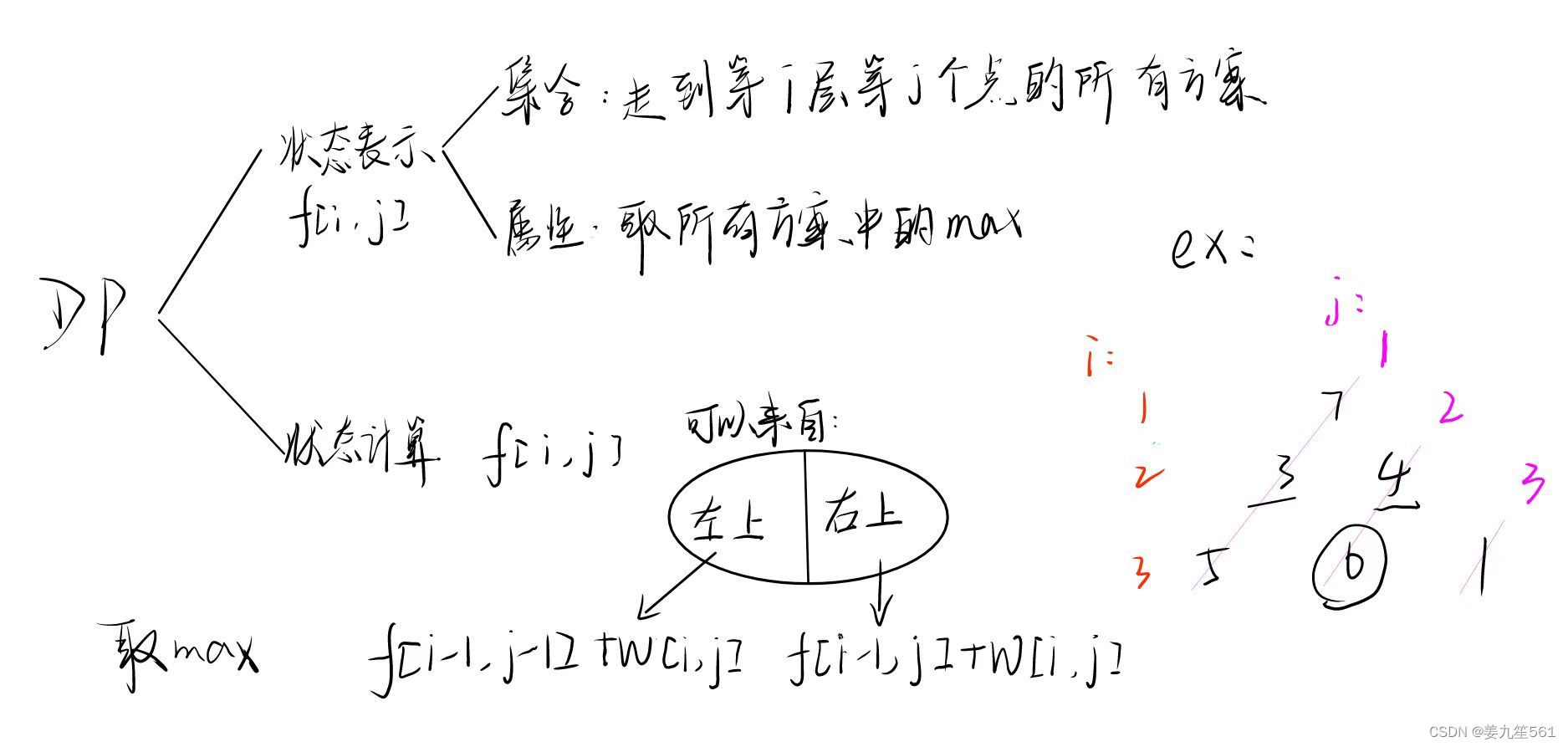
题目：数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

        73   88   1   02   7   4   4
4   5   2   6   5

输入格式

第一行包含整数 n，表示数字三角形的层数。

接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。

输出格式

输出一个整数，表示最大的路径数字和。

数据范围

1≤n≤500,
−10000≤三角形中的整数≤10000

输入样例：

5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

输出样例：

30

import java.io.*;
import java.util.*;class Main{static int N = 510,INF = 0x3f3f3f3f;static int[][] w = new int[N][N];static int[][] f = new int[N][N];public static void main(String[] args) throws IOException{BufferedReader in = new BufferedReader(new InputStreamReader(System.in));int n = Integer.parseInt(in.readLine());for(int i=1;i<=n;i++){String[] s = in.readLine().split(" ");for(int j=1;j<=i;j++)w[i][j] = Integer.parseInt(s[j-1]);}// 因为整数可能为负，所以将f[][]初始化为负无穷，注意，要向外多初始化一点，因为有些点的右上或者左上是没有值的for(int i=0;i<=n+1;i++)Arrays.fill(f[i],-INF);f[1][1] = w[1][1]; // 第一个// DPfor(int i=2;i<=n;i++){for(int j=1;j<=i;j++){f[i][j] = Math.max(f[i-1][j-1]+w[i][j],f[i-1][j]+w[i][j]);}}// 取最后一行的最大值int res = -INF;for(int i=1;i<=n;i++) res = Math.max(res,f[n][i]);System.out.println(res);}
}