KMP算法
KMP算法解决的问题
KMP算法用来解决字符串匹配问题: 找到长串中短串出现的位置.
KMP算法思路
暴力比较与KMP的区别
- 暴力匹配: 对长串的每个位,都从头开始匹配短串的所有位.

- KMP算法: 将短字符串前后相同的部分存储在 n e x t next next数组里,让之前匹配过的信息指导之后的匹配.
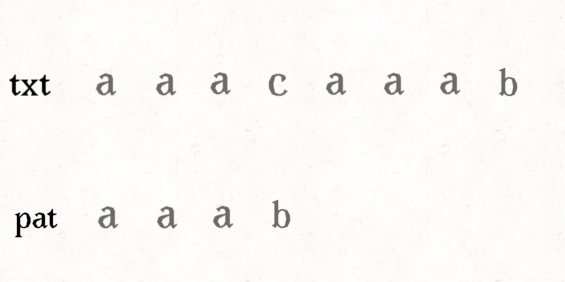
n e x t next next数组及其求法
n e x t next next数组体现字符串某位前边子串最长匹配前缀和最长匹配后缀的匹配长度(可以有交叉). n e x t [ i ] next[i] next[i]表示第 i i i位前边的最长匹配后缀对应的最长匹配前缀的后一位.
下面是一个next数组的例子:

next数组的求法
n e x t next next数组的求法用到了递推思想:
-
第 0 0 0位前边没有匹配前后缀,因此 n e x t [ 0 ] = − 1 next[0]=-1 next[0]=−1
-
第 1 1 1位前缀字符串的长度为1,因此 n e x t [ 1 ] = 0 next[1]=0 next[1]=0
-
站在第 p o s pos pos位上,就要考虑以第 i − 1 i-1 i−1位结尾的最长匹配(也就是不断地求 n u m s [ p o s − 1 ] nums[pos-1] nums[pos−1]与 n e x t [ n e x t [ . . . n e x t [ p o s − 1 ] ] ] next[next[...next[pos-1]]] next[next[...next[pos−1]]]之间的关系):

- 将 c n cn cn指针指向前一个匹配后缀的下一位,即 c n = n e x t [ p o s − 1 ] cn=next[pos-1] cn=next[pos−1]
- 若前一个匹配后缀的下一位字符刚好与待匹配字符相同,即 m s [ c n ] = = m s [ p o s − 1 ] ms[cn]==ms[pos-1] ms[cn]==ms[pos−1],则更新next数组,将 n e x t [ p o s ] next[pos] next[pos]指向 c n cn cn的下一位 n e x t [ p o s ] = c n + 1 next[pos]=cn+1 next[pos]=cn+1
- 若前一个匹配后缀的下一位字符与待匹配字符不同,即 m s [ c n ] ! = m s [ p o s − 1 ] ms[cn]!=ms[pos-1] ms[cn]!=ms[pos−1],则应该找前一个匹配数组,即 c n = n e x t [ c n ] cn=next[cn] cn=next[cn]
- 若最终找到 c n = = − 1 cn==-1 cn==−1也没找到,则 p o s − 1 pos-1 pos−1位实在没有匹配后缀了,将其 n e x t next next数组置 0 0 0,即 n e x t [ p o s ] = 0 next[pos]=0 next[pos]=0
// 计算ms字符串的next[]数组
public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[] { -1 };}int[] next = new int[ms.length];next[0] = -1; // 第0位前边没有前缀字符串,因此返回-1next[1] = 0; // 第1位前缀字符串的长度为1,若该位匹配不上则只能去匹配首位,因此返回0// 从第2位开始,递推出后面位的next[]值for (int pos = 2; pos < ms.length; pos++) {// 一直向前找前边位的匹配前缀且该前缀的后一位与本位相同int cn = next[pos - 1];while (cn != -1 && ms[cn] != ms[pos-1]) {// 将前缀的后一位与当前位的前一位进行对比cn = next[cn];}// 判断是否能找到匹配前缀//if (cn != -1) {// // 若能找到匹配前后缀,则返回匹配前缀的后一位// next[pos] = cn + 1;//} else {// // 若找不到匹配前后缀,返回-1// next[pos] = 0;//}// 上述判断语句可以简化为一句next[pos] = cn + 1;}return next;
}
在写入 n e x t next next数组的 p o s pos pos位时要注意: 匹配前缀延伸的时候,要判断的是 m s [ c n ] 与 m s [ p o s − 1 ] ms[cn]与ms[pos-1] ms[cn]与ms[pos−1]之间是否相等
(因为 n e x t next next数组保存的是本位前一位的匹配前缀的下一位,因此 m s [ c n ] ms[cn] ms[cn]指向匹配前缀的下一位, m s [ p o s − 1 ] ms[pos-1] ms[pos−1]指向上次计算未进行匹配的位)
题目代码
P3375 【模板】KMP
#include <bits/stdc++.h>
using namespace std;
int kmp[1000005];
int la,lb,j;
char a[1000005],b[1000005];
int main() {cin>>a+1;cin>>b+1;la=strlen(a+1);lb=strlen(b+1);for (int i=2; i<=lb; i++) {while(j&&b[i]!=b[j+1])j=kmp[j];if(b[j+1]==b[i])j++;kmp[i]=j;}j=0;for(int i=1; i<=la; i++) {while(j>0&&b[j+1]!=a[i])j=kmp[j];if (b[j+1]==a[i])j++;if (j==lb) {cout<<i-lb+1<<endl;j=kmp[j];}}for (int i=1; i<=lb; i++)cout<<kmp[i]<<" ";return 0;
}
Manacher算法
Manacher算法解决的问题
Manacher算法用来寻找字符串的最长回文子串.
回文串的相关概念
- 回文右边界: 当前所有回文串中,回文右边界所能到达的最右位置.
- 回文右边界中心: 以回文右边界结尾的最长回文串的回文中心.
Manacher算法思路
从第一位开始,遍历字符串的所有位.初始时回文右边界为-1.
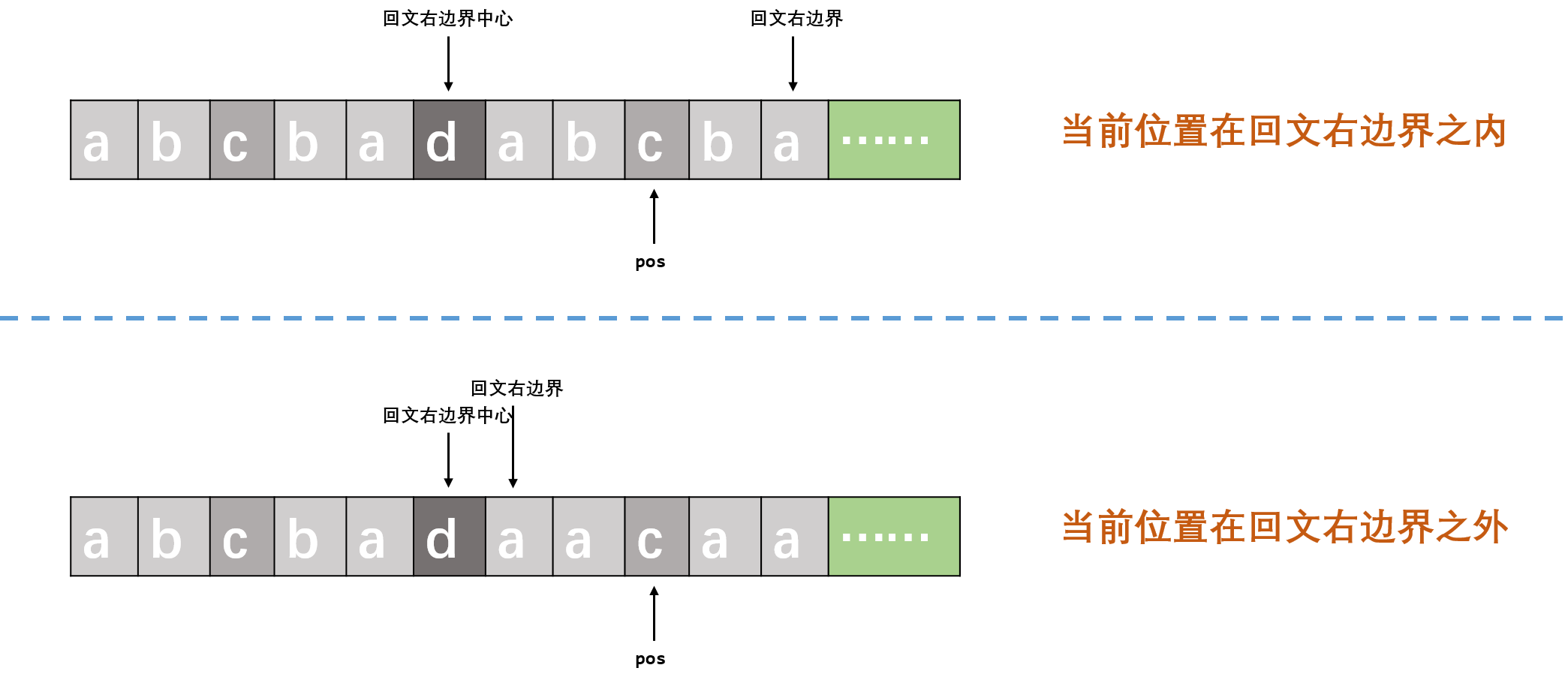
当遍历到第pos位时,有以下两种情况
- p o s pos pos不在回文右边界 r i g h t B o r d e r rightBorder rightBorder以内 ( p o s > r i g h t B o r d e r ) (pos > rightBorder) (pos>rightBorder): 以该位为中心向两边暴力扩展回文串.
- p o s pos pos在回文右边界 r i g h t B o r d e r rightBorder rightBorder以内 ( p o s < = r i g h t B o r d e r ) : (pos <= rightBorder): (pos<=rightBorder):找到回文右边界中心 r i g h t C e n t e r rightCenter rightCenter,对应的回文左边界,以及 p o s pos pos关于回文右边界中心的对称点 p o s ′ pos' pos′.这样 p o s ′ pos' pos′的回文半径可以用来指导 p o s pos pos的回文半径
- 若 p o s ′ pos' pos′回文串关于 r i g h t C e n t e r rightCenter rightCenter的对称串在回文右边界以内 ( p o s + c u r R a d i u s [ p o s ] − 1 < = r i g h t B o r d e r ) (pos + curRadius[pos] -1 <= rightBorder) (pos+curRadius[pos]−1<=rightBorder),说明 p o s pos pos的回文半径与 p o s ′ pos' pos′的回文半径相同
- 若 p o s ′ pos' pos′回文串关于 r i g h t C e n t e r rightCenter rightCenter的对称串在回文右边界以外 ( p o s + c u r R a d i u s [ p o s ] − 1 > r i g h t B o r d e r ) (pos + curRadius[pos] -1 > rightBorder) (pos+curRadius[pos]−1>rightBorder),由对称性可知,对称串超出回文右边界的部分一定不能构成以 p o s pos pos为中心的回文.因此 p o s pos pos的回文半径即为 p o s pos pos到回文右边界之间.
在遍历过程中维护的回文右边界串并不一定是最长回文子串,如上面演示图中第一种情况为例: 遍历结束时,回文右边界串为" a b c b a abcba abcba",最长回文子串为" a b c b a d a b c b a abcbadabcba abcbadabcba"
题目代码
P3805 【模板】manacher
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=22000010;
char fr[maxn],s[maxn];
ll len[maxn];
int main()
{scanf("%s",fr);ll frlen=strlen(fr),count1=0;s[count1++]='*';for(ll i=0;i<frlen;i++){s[count1++]='#';s[count1++]=fr[i];}s[count1++]='#';s[count1++]='!';len[0]=0;ll mx=0,ans=0,id=0;for(ll i=1;i<count1;i++){if(i<mx)len[i]=min(mx-i,len[2*id-i]);elselen[i]=1;while(s[i-len[i]]==s[i+len[i]])len[i]++;if(len[i]+i>mx){mx=len[i]+i;id=i;ans=max(ans,len[i]-1);}}printf("%lld",ans);return 0;
}


| 121. 买卖股票的最佳时机 122.买卖股票的最佳时机II)













:用户操作)


:Python语言介绍及第一个Pyhon程序)