一、PCD点云数据存储格式的进一步认识
(一)PCD点云存储格式相较于其它存储格式(如PLY、STL、OBJ、X3D等)的优势[1]
(1)具有存储和处理有组织的点云数据集的能力,这对于实时应用和增强现实及机器人等研究领域十分重要;
(2)二进制的mmap/munmap可能是最快加载和存储数据至磁盘的方式(在实验中,我发现Linux系统下基于PCL/Open3D库读取数据较Windows系统快。后经查阅了解到,二进制格式的点云数据读取是基于pcl::PointCloud.points array/vector的完全临时复制。在Linux系统中,为了尽可能最快地读取数据而采用mmap/munmap操作);
(3)能够存储不同的数据类型(支持所有基础类型,如char、short、int、float和double)以达到高效处理和存储复杂的点云数据。无效的点云维度通常被存储为NAN类型,但自从PCL 1.0.1开始,NAN类型字符被替换为nan表示;
(4)支持n-D直方图特征描述符,这对三维感知和计算机视觉应用十分重要;
(5)通过控制文件格式,PCD存储格式可以最好地匹配PCL库,从而在PCL应用中获得最高的性能表现。与此同时,PCL应用运行不需要将各类数据格式都作为PCL的基础格式且不需要耗费额外的时间在数据转换函数上,以提高时空效率。
(二)PCD文件格式头解析[1]
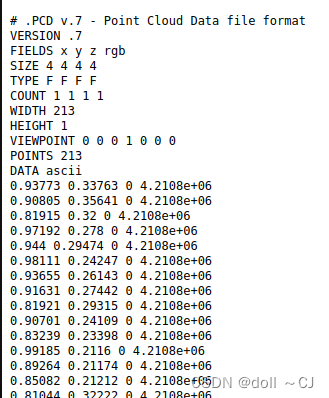
PCD文件的格式头用于识别和表明存储点云数据的确定属性,格式头必须为ASCII编码且每一个属性实体被换行符(\n)分隔。值得注意的是,视点位置较为重要,视点将会被用于不同坐标系统之间的转换或者辅助特征计算(如局部表面法线需要一个不变的视线辅助计算保持一致性,即法线定向[8])。
(1)VERSION PCD格式文件的版本号
(2)FIELDS 每一维度的特定属性标识名字
(3)SIZE 每一维数据存储的字节数(unsigned char/char为1字节;unsigned short/short为2字节;unsigned int/int/float为4字节;double为8字节)
(4)TYPE 每一维度表示字符的数据类型(I-int8(char)/int16(short)/int32(int) U- uint8(unsigned char)/uint16(unsigned short)/uint32(unsigned int) F-float)
(5)COUNT 一个维度的表示元素数量。默认不表示COUNT情况,其为1
(6)WIDTH 一行记录的点的数量
(7)HEIGHT (有/无组织存储标记)若无组织存储为1,否则为点云数据存储的行数
(8)VIEWPOINT 点云数据的视点(tx ty tz qw qx qy qz)
(9)POINTS 存储点云的总体数量(与WIDTH*HEIGHT一致)
(10)DATA 特定数据格式存储的点云数据
二、基于KDTree的点云结构化组织
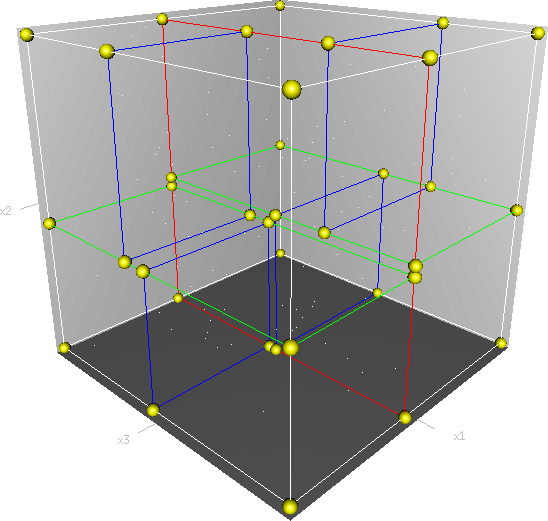
在计算机科学里,k-d树(k-dimensional tree)是在k维欧几里德空间组织点的数据结构,是空间二叉树的一种特殊情况。k-d树可以使用在多种应用场合,如多维键值搜索(如范围搜索及最邻近搜索)。k-d树是每个叶子节点都为k维点的二叉树,所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点,节点右边的子树代表在超平面右边的点。选择超平面的方法如下:每个节点都与k维中垂直于超平面的那一维有关[2]。
一个三维树。第一次划分(红色)把根节点(白色)划分成两个节点,然后它们分别再次被划分(绿色)为两个子节点。最后这四个子节点的每一个都被划分(蓝色)为两个子节点。因为没有更进一步的划分,最后得到的八个节点称为叶子节点,如图二所示。
三、点云数据的三维格网化/体素化
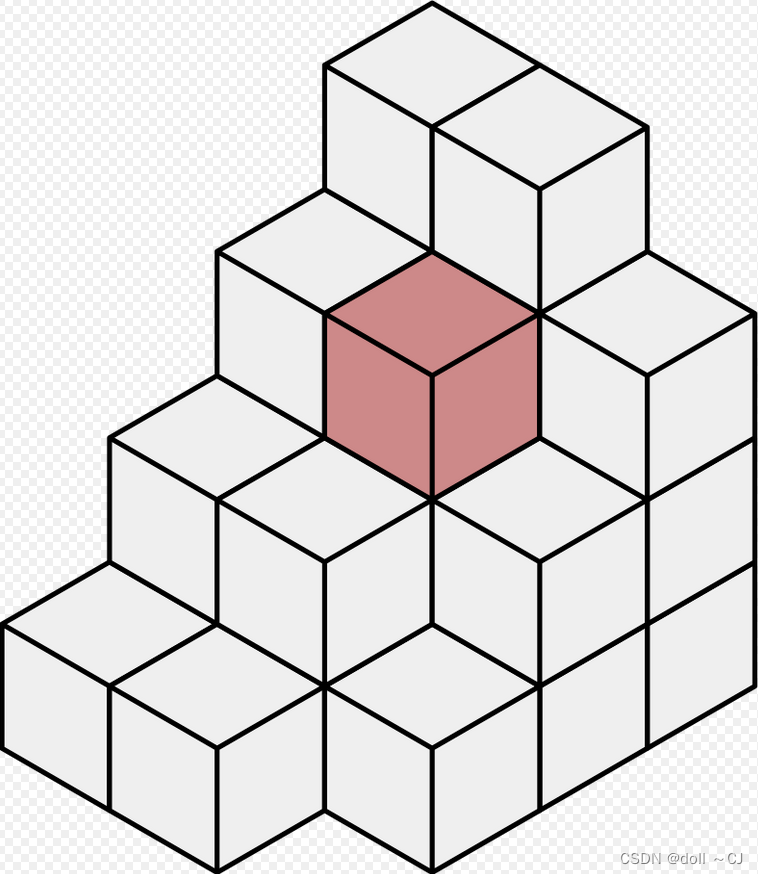
体素(Voxel)是体积像素的简称。概念上类似二维空间的最小单位—像素,像素用于二维图像。体积像素一如其名,是数字资料于三维空间分割上的最小单位[4]。点云数据三维格网化通常用于基于体素的深度学习数据预处理、局部相对特征计算以及投影。
四、基于的Octree的点云结构化组织
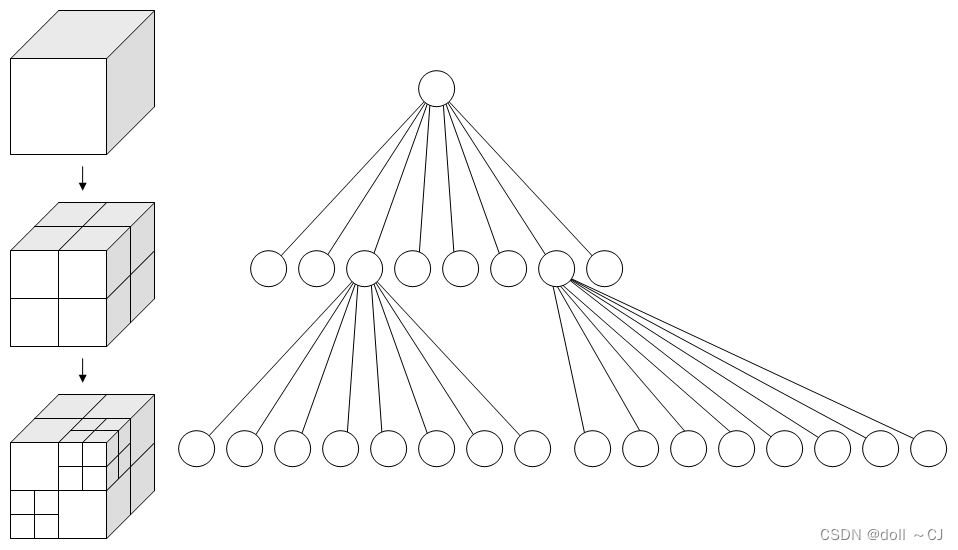
八叉树(Octree)是一种树形数据结构,每个内部节点都正好有八个子节点。八叉树常用于分割三维空间,将其递归细分为八个卦限。八叉树是四叉树在三维空间中的对应,在三维图形、三维游戏引擎等领域有很多应用。八叉树的每个节点都可以代表一个空间,对应的八个子节点则将这个空间细分为八个卦限。点域(point region,简称PR)八叉树的节点中都存储着一个三维点,即该节点对应区域的“中心”,也是八个子节点对应区域中的一个角落。矩阵(matrix based,简称MX)八叉树中,节点只记录区域范围,对应的中心点坐标需要从区域范围推算。因此,PR八叉树的根节点可以表示无限大的空间;而MX八叉树的根节点只能表示有限空间,这样才可以得到隐含的中心点[6]。
参考资料:
[1] The PCD (Point Cloud Data) file format — Point Cloud Library 1.14.0-dev documentation
[2] https://en.wikipedia.org/wiki/K-d_tree
[3] KDTree - Open3D 0.18.0 documentation
[4] https://en.wikipedia.org/wiki/Voxel
[5] Voxelization - Open3D 0.18.0 documentation
[6] https://en.wikipedia.org/wiki/Octree
[7] Octree - Open3D 0.18.0 documentation
[8] Open3D 法线估计(2)——法线定向_open3d法向量定向-CSDN博客
[9] Open3D KDTree的使用_open3d使用kdtree-CSDN博客
[10] Open3D 从点云中构建八叉树_根据空间点构造八叉树-CSDN博客
)




)
)

)

)








