系列文章目录

代码随想录算法训练营第一天|数组理论基础，704. 二分查找，27. 移除元素
代码随想录算法训练营第二天|977.有序数组的平方 ，209.长度最小的子数组 ，59.螺旋矩阵II
代码随想录算法训练营第三天|链表理论基础，203.移除链表元素，707.设计链表，206.反转链表
代码随想录算法训练营第四天|24. 两两交换链表中的节点，19.删除链表的倒数第N个节点，面试题 02.07. 链表相交，142.环形链表II，总结
代码随想录算法训练营第五天|哈希表理论基础，242.有效的字母异位词，349. 两个数组的交集，202. 快乐数，1. 两数之和
代码随想录算法训练营第六天|454.四数相加II，383. 赎金信，15. 三数之和，18. 四数之和，总结
代码随想录算法训练营第七天|344.反转字符串，541. 反转字符串II，卡码网：54.替换数字，151.翻转字符串里的单词，卡码网：55.右旋转字符串
代码随想录算法训练营第八天|28. 实现 strStr()，459.重复的子字符串，字符串总结，双指针回顾
代码随想录算法训练营第九天|理论基础，232.用栈实现队列，225. 用队列实现栈
代码随想录算法训练营第十天|20. 有效的括号，1047. 删除字符串中的所有相邻重复项，150. 逆波兰表达式求值
代码随想录算法训练营第十一天|239. 滑动窗口最大值，347.前 K 个高频元素，总结
代码随想录算法训练营第十二天|理论基础，递归遍历，迭代遍历，统一迭代
代码随想录算法训练营第十三天|层序遍历10，226.翻转二叉树，101.对称二叉树
代码随想录算法训练营第十四天|104.二叉树的最大深度，559.n叉树的最大深度，111.二叉树的最小深度，222.完全二叉树的节点个数
代码随想录算法训练营第十五天|110.平衡二叉树，257. 二叉树的所有路径，404.左叶子之和
代码随想录算法训练营第十六天|513.找树左下角的值，112. 路径总和，113.路径总和ii，106.从中序与后序遍历序列构造二叉树，105.从前序与中序遍历序列构造二叉树
代码随想录算法训练营第十七天|654.最大二叉树，617.合并二叉树，700.二叉搜索树中的搜索，98.验证二叉搜索树
代码随想录算法训练营第十八天|530.二叉搜索树的最小绝对差，501.二叉搜索树中的众数，236. 二叉树的最近公共祖先
代码随想录算法训练营第十九天|235. 二叉搜索树的最近公共祖先，701.二叉搜索树中的插入操作，450.删除二叉搜索树中的节点
代码随想录算法训练营第二十天|669. 修剪二叉搜索树，108.将有序数组转换为二叉搜索树，538.把二叉搜索树转换为累加树，总结篇
代码随想录算法训练营第二十一天|回溯算法理论基础，77. 组合
代码随想录算法训练营第二十二天|216.组合总和III，17.电话号码的字母组合
代码随想录算法训练营第二十三天|39. 组合总和，40.组合总和II，131.分割回文串
代码随想录算法训练营第二十四天|93.复原IP地址，78.子集，90.子集II
代码随想录算法训练营第二十五天|491.递增子序列，46.全排列，47.全排列 II
代码随想录算法训练营第二十六天|332.重新安排行程，51. N皇后，37. 解数独，总结
代码随想录算法训练营第二十七天|贪心算法理论基础，455.分发饼干，376. 摆动序列，53. 最大子序和
代码随想录算法训练营第二十八天|122.买卖股票的最佳时机II，55. 跳跃游戏，45.跳跃游戏II
代码随想录算法训练营第二十九天|1005.K次取反后最大化的数组和，134. 加油站，135. 分发糖果
代码随想录算法训练营第三十天|860.柠檬水找零，406.根据身高重建队列，452. 用最少数量的箭引爆气球
代码随想录算法训练营第三十一天|435. 无重叠区间，763.划分字母区间，56. 合并区间
代码随想录算法训练营第三十二天|738.单调递增的数字，968.监控二叉树，总结
代码随想录算法训练营第三十三天|动态规划理论基础，509. 斐波那契数，70. 爬楼梯，746. 使用最小花费爬楼梯
代码随想录算法训练营第三十四天|62.不同路径，63. 不同路径 II
代码随想录算法训练营第三十五天|343. 整数拆分，96.不同的二叉搜索树
代码随想录算法训练营第三十六天|背包理论基础，416. 分割等和子集
代码随想录算法训练营第三十七天|1049. 最后一块石头的重量 II，494. 目标和，474.一和零
代码随想录算法训练营第三十八天|完全背包，518. 零钱兑换 II，377. 组合总和 Ⅳ
代码随想录算法训练营第三十九天|70. 爬楼梯 （进阶），322. 零钱兑换，279.完全平方数
代码随想录算法训练营第四十天|139.单词拆分，多重背包介绍，背包问题总结篇！

---

198.打家劫舍

题目链接： 198.打家劫舍
题目内容： 你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
视频讲解： 动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍

动态规划问题的五步曲：

• 确定dp数组（dp table）以及下标的含义：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]

• 确定递推公式：dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])

• dp数组如何初始化：dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1])

• 确定遍历顺序：从前到后遍历

• 举例推导dp数组

class Solution:def rob(self, nums: List[int]) -> int:if len(nums) == 0:return 0if len(nums) == 1:return nums[0]dp=[0]*len(nums)dp[0]=nums[0]dp[1]=max(nums[0],nums[1])for i in range(2,len(nums)):dp[i]=max(dp[i-1],dp[i-2]+nums[i])return dp[-1]

213.打家劫舍II

题目链接： 213.打家劫舍II
题目内容： 你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。
视频讲解： 动态规划，房间连成环了那还偷不偷呢？| LeetCode：213.打家劫舍II

与打家劫舍1的区别：打家劫舍II中的房屋连成环了，第一个房屋和最后一个房屋是紧挨着的。
对于一个数组，成环的话主要有如下三种情况：

• 情况一：考虑不包含首尾元素
• 情况二：考虑包含首元素，不包含尾元素
• 情况三：考虑包含尾元素，不包含首元素

而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了。

动态规划问题的五步曲：

• 确定dp数组（dp table）以及下标的含义：爬到有i个台阶的楼顶，有dp[i]种方法

• 确定递推公式：dp[i] += dp[i - j]

• dp数组如何初始化：dp[0] = 1，下标非0的dp[j]初始化为0

• 确定遍历顺序：这是背包里求排列问题，即：1、2 步 和 2、1 步都是上三个台阶，但是这两种方法不一样！所以需将target放在外循环，将nums放在内循环。每一步可以走多次，这是完全背包，内循环需要从前向后遍历。

• 举例推导dp数组

class Solution:def rob(self, nums: List[int]) -> int:if len(nums)==0:return 0if len(nums)==1:return nums[0]#情况二result1=self.robRange(nums,0,len(nums)-2)#情况三result2=self.robRange(nums,1,len(nums)-1)return max(result1,result2)def robRange(self,nums,start,end):if end==start:return nums[start]#初始化prev_max=nums[start] curr_max=max(nums[start],nums[start+1])for i in range(start+2,end+1):temp=curr_maxcurr_max=max(prev_max+nums[i],curr_max)prev_max=tempreturn curr_max

337.打家劫舍III

题目链接： 337.打家劫舍III
题目内容： 小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。
视频讲解： 动态规划，房间连成树了，偷不偷呢？| LeetCode：337.打家劫舍3

动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组，记录当前节点偷与不偷所得到的的最大金钱。

递归三部曲：

• 确定递归函数的参数和返回值：要求一个节点 偷与不偷的两个状态所得到的金钱，那么参数为当前节点，返回值就是一个长度为2的数组。这里的返回数组就是dp数组。

dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。所以本题dp数组就是一个长度为2的数组！（在递归的过程中，系统栈会保存每一层递归的参数）

• 确定终止条件：在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回[0,0]（这也相当于dp数组的初始化）
• 确定遍历顺序：后序遍历。因为要通过递归函数的返回值来做下一步计算。
  通过递归左节点，得到左节点偷与不偷的金钱。
  通过递归右节点，得到右节点偷与不偷的金钱。
• 确定单层递归的逻辑：
  • 如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]
  • 如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1])
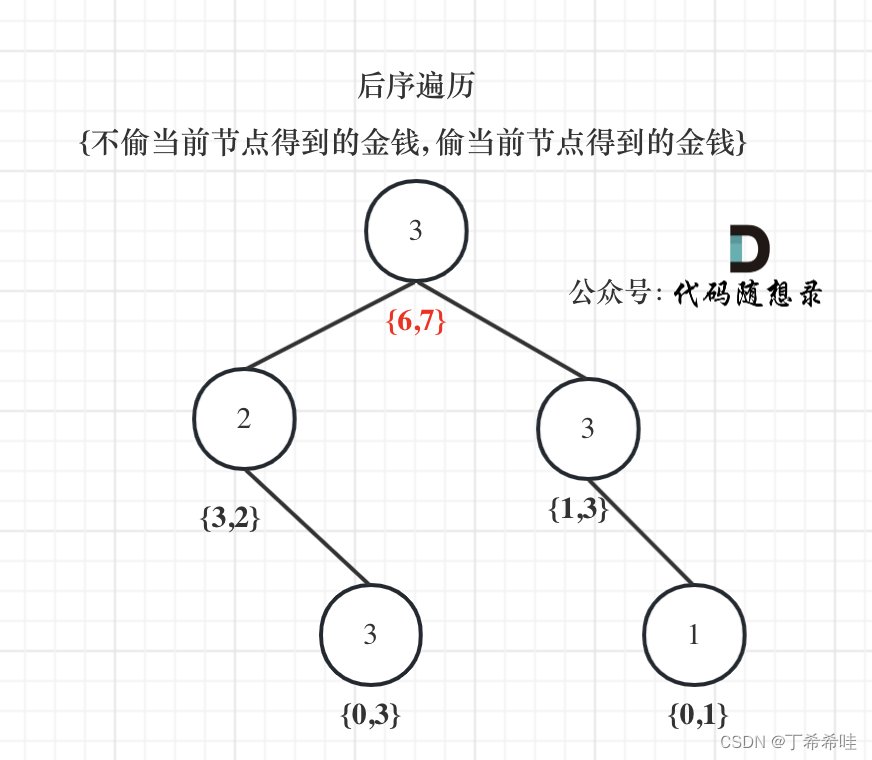
  • 最后当前节点的状态就是{val2, val1}; 即：{不偷当前节点得到的最大金钱，偷当前节点得到的最大金钱}
• 举例推导dp数组

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:dp=self.traversal(root)return max(dp)def traversal(self,node):#递归终止条件if not node:return (0,0)#左节点left=self.traversal(node.left)#右节点right=self.traversal(node.right)#不偷当前节点var1=max(left[0],left[1])+max(right[0],right[1])#偷当前节点var2=node.val+left[0]+right[0]return (var1,var2)