数据结构:树 3月1日 – 天气:晴
之前在B站看的视频讲的是在太过简单,弃了。现在换了新的视频继续,后续会重新看前面的视频补过来。https://www.bilibili.com/video/BV1pT4m1S7uH/
1. 树的基本概念

需要注意的是:
- 并不是在同一层上的所有节点都互为兄弟节点。而是具有相同双亲的节点成为兄弟节点
- 注意有序树和无序树的概念,并且二叉树是有序树
2. 二叉树
2.1 二叉树的定义
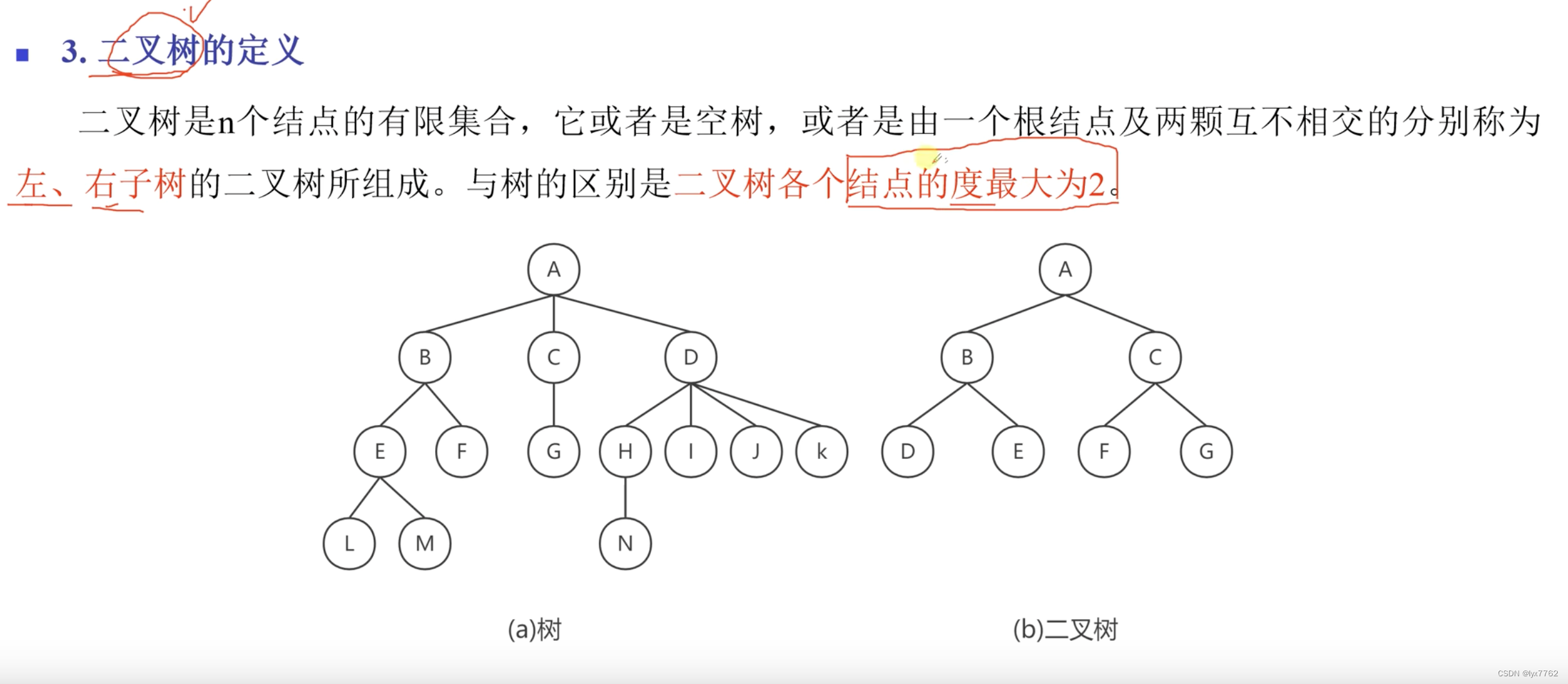
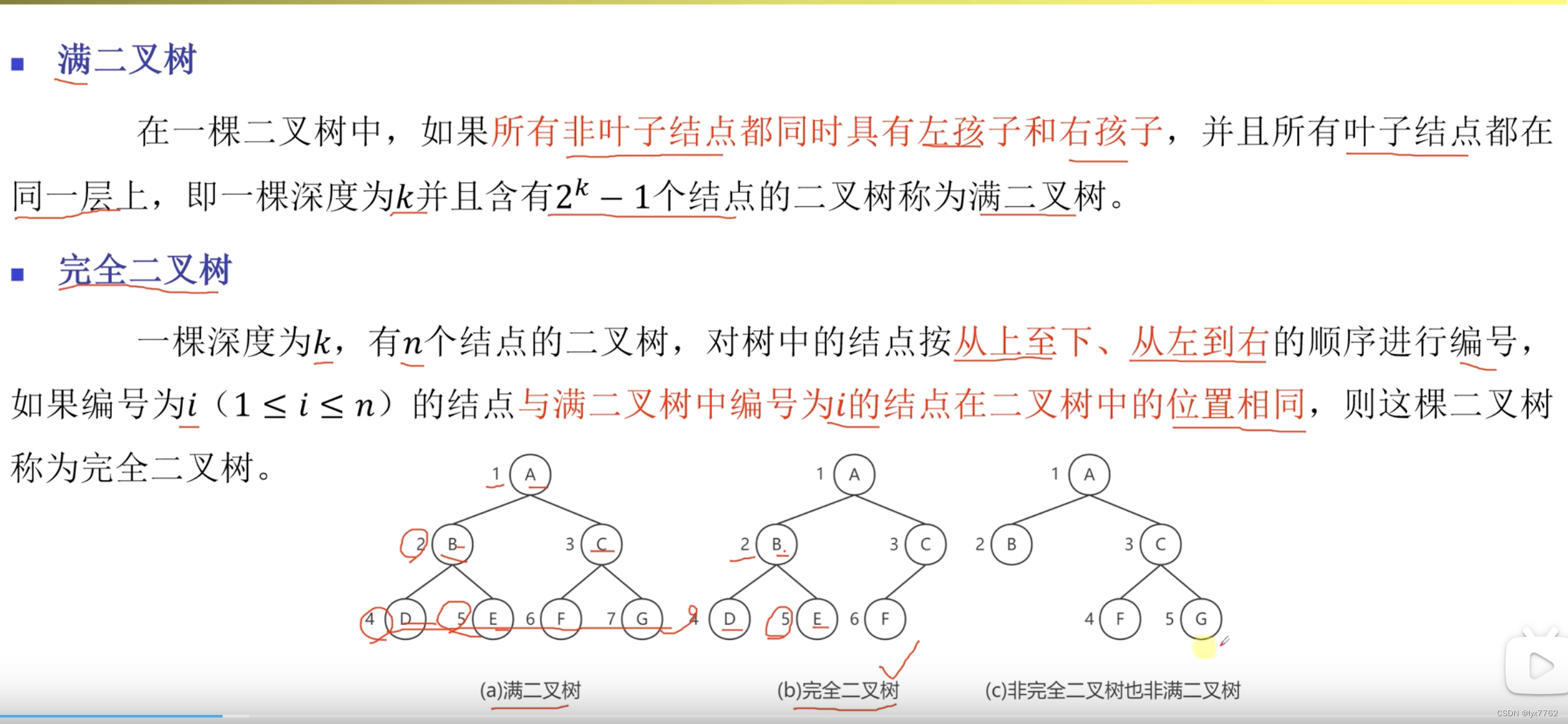
二叉树是有序树!
2.2 二叉树的性质

关于第三条性质的证明:
首先需要知道一个概念:对于任意一个树,满足“节点个数=分支数量+1”。其中分支数量就是上图红色部分的横线。
因此对于二叉树:
- 假设度为0的节点为
n0,度为1的节点为n1,度为0的节点为n1- 那么
节点个数=n0+n1+n2分支个数为=n0×0+n1×1+n2×2- 根据上述公式可以得出:
n0+n1+n2=0×0+n1×1+n2×2+1- 化简后得到
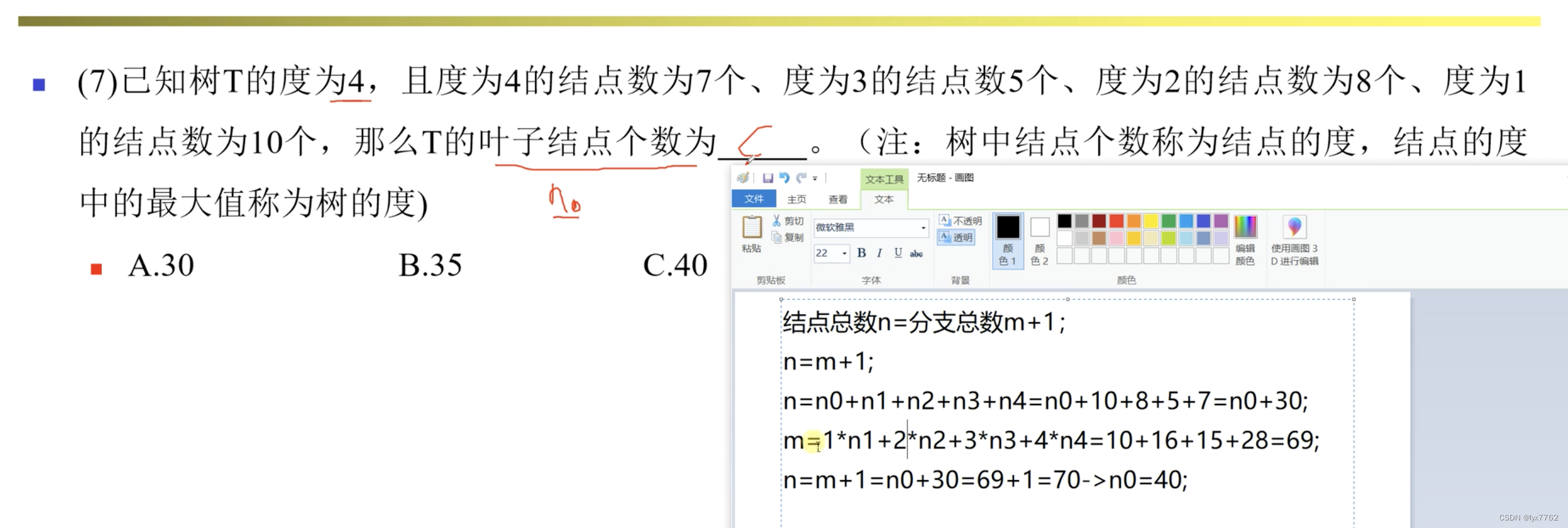
n0=n2+1关于上述性质,有一个例题:
2.3 二叉树的存储结构
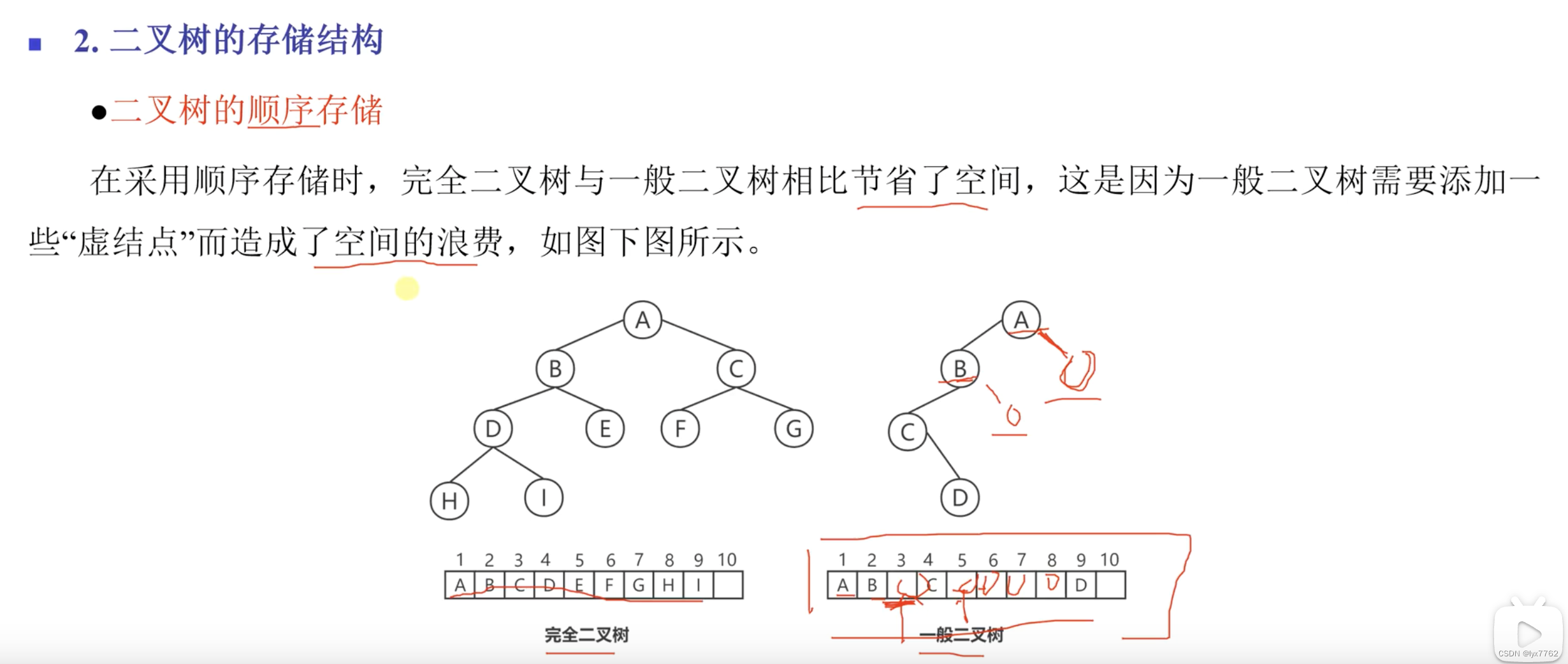
对于完全二叉树和满二叉树,这种方式比较合适,可以根据之前二叉树性质的公式直接计算出某一个节点的孩子节点的存储地址,进而可以直接访问。
但是对于普通的二叉树来说,会浪费大量的存储空间

针对二叉树的链式存储,每一个节点都有两个指针域,但是实际上这些空间并不会完全利用,实际利用到的指针域数量为:
- 假设二叉树中有n个节点,那么所有的指针域总数为2n
- 根据
分支总数+1=节点个数公式,可以得到分支总是为分支总数=节点个数-1,并且分支个数=利用的指针域个数- 所以实际使用的指针域个数为
n-1- 则没有使用的指针域个数为
2n-(n-1)=n+1因此为了充分利用空闲指针域,提出了线索二叉树,结构如下:
2.4 二叉树的遍历方式

2.5 最优二叉树

如何构建哈夫曼树


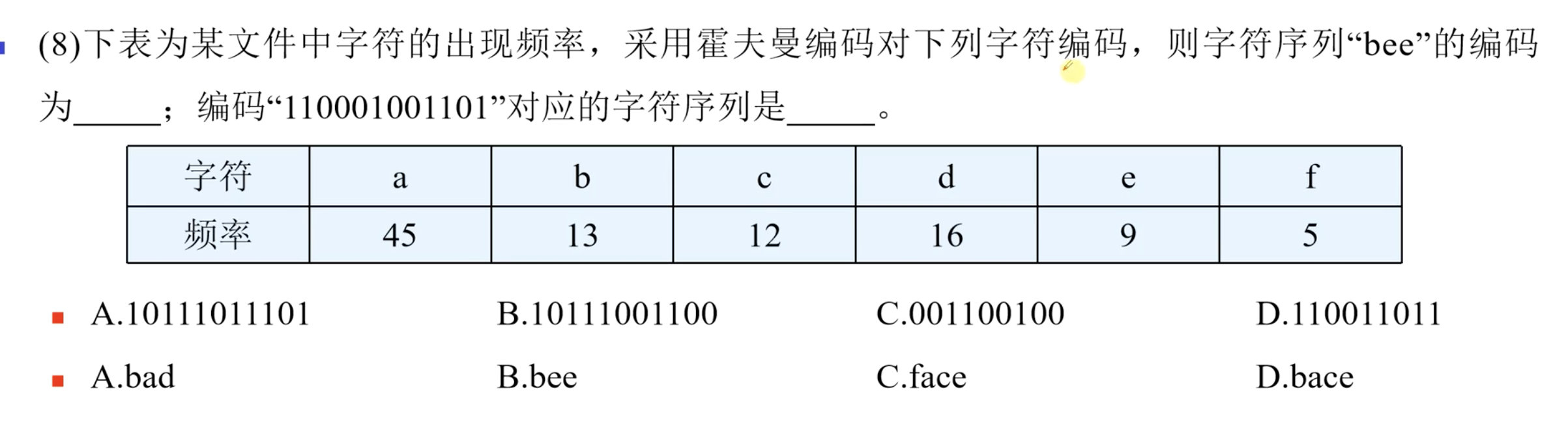

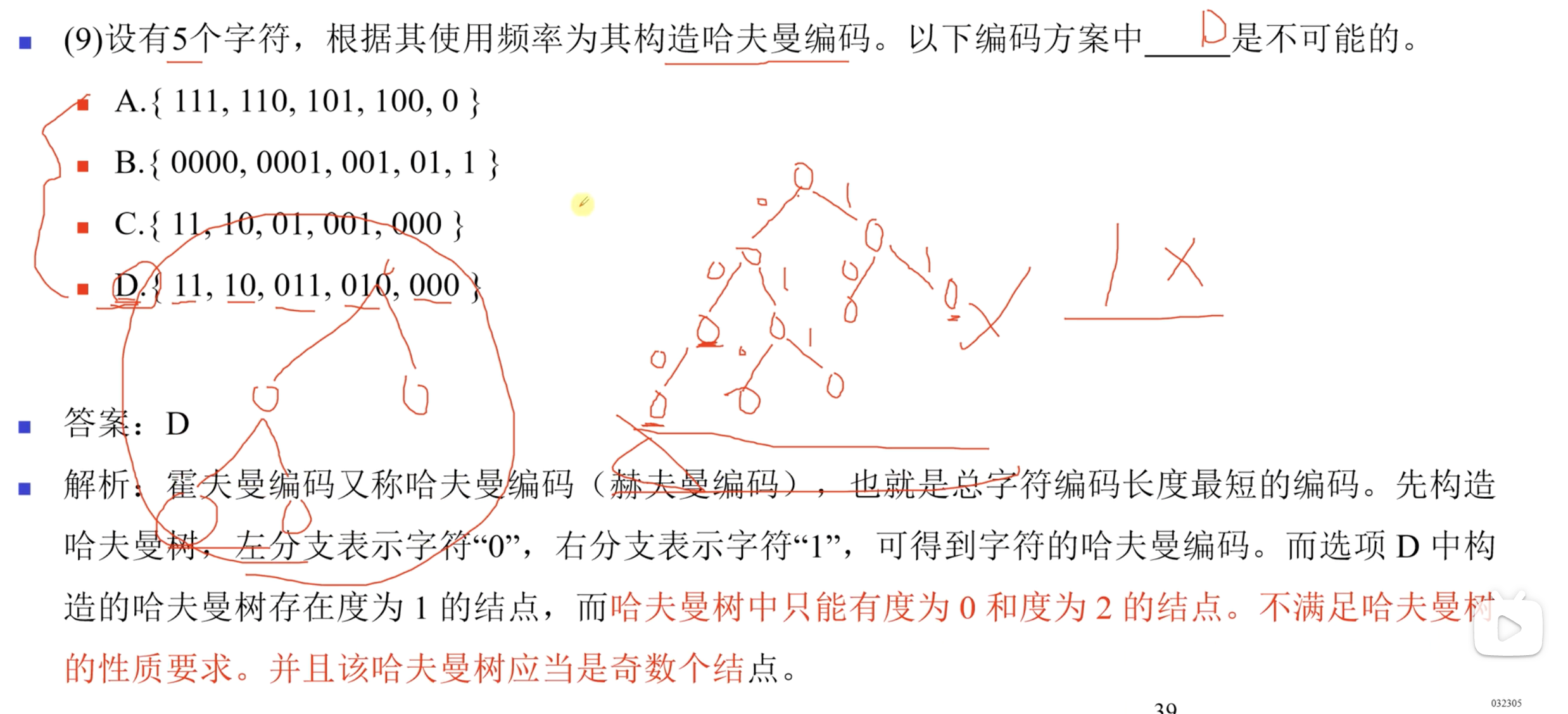
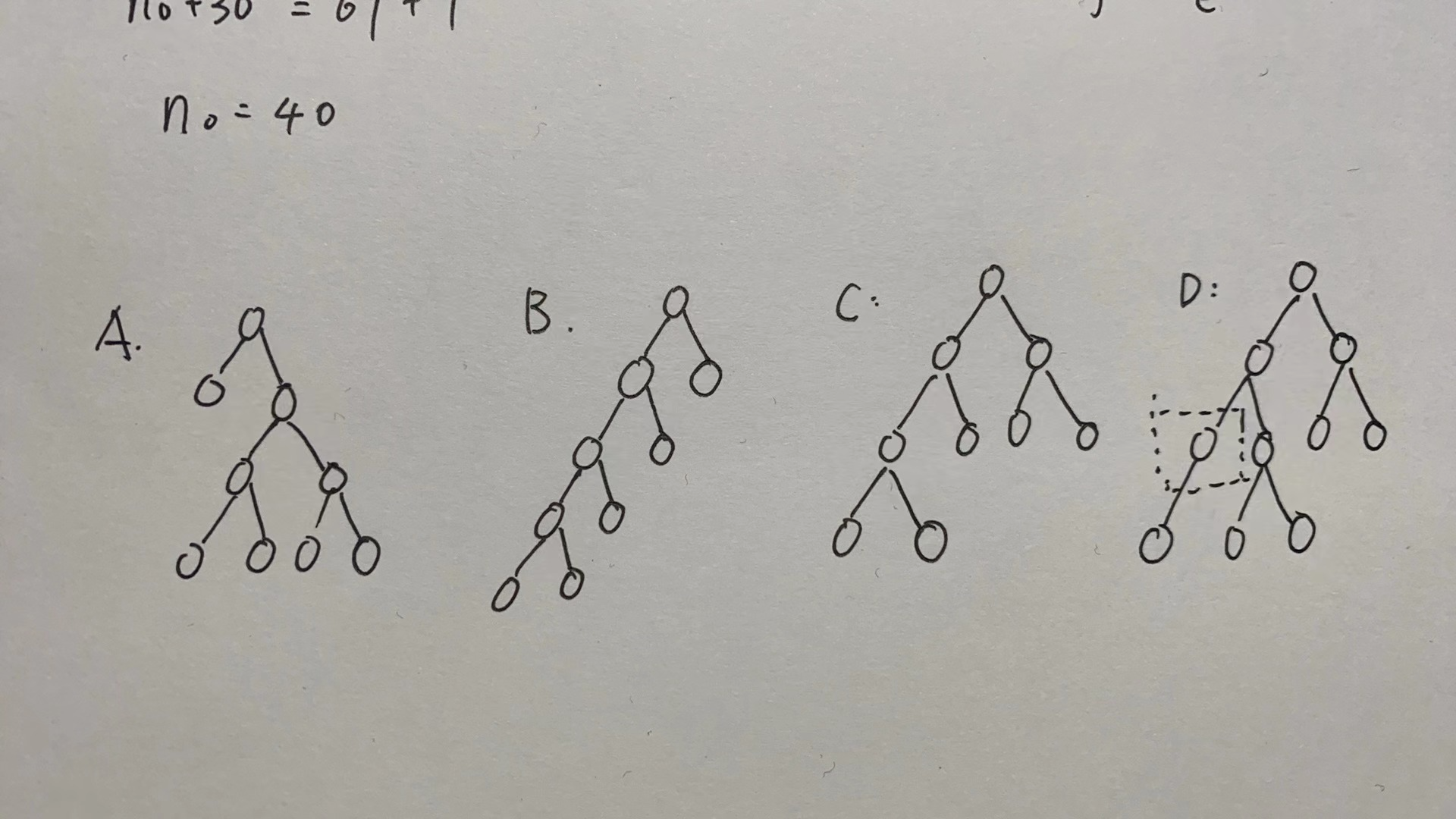
需要注意的是,哈夫曼树只有度为0和度为2的节点。
因为我们构建哈夫曼的操作都是两个节点构成一个新节点,所以不可能存在度为1的节点。

3. 树和森林
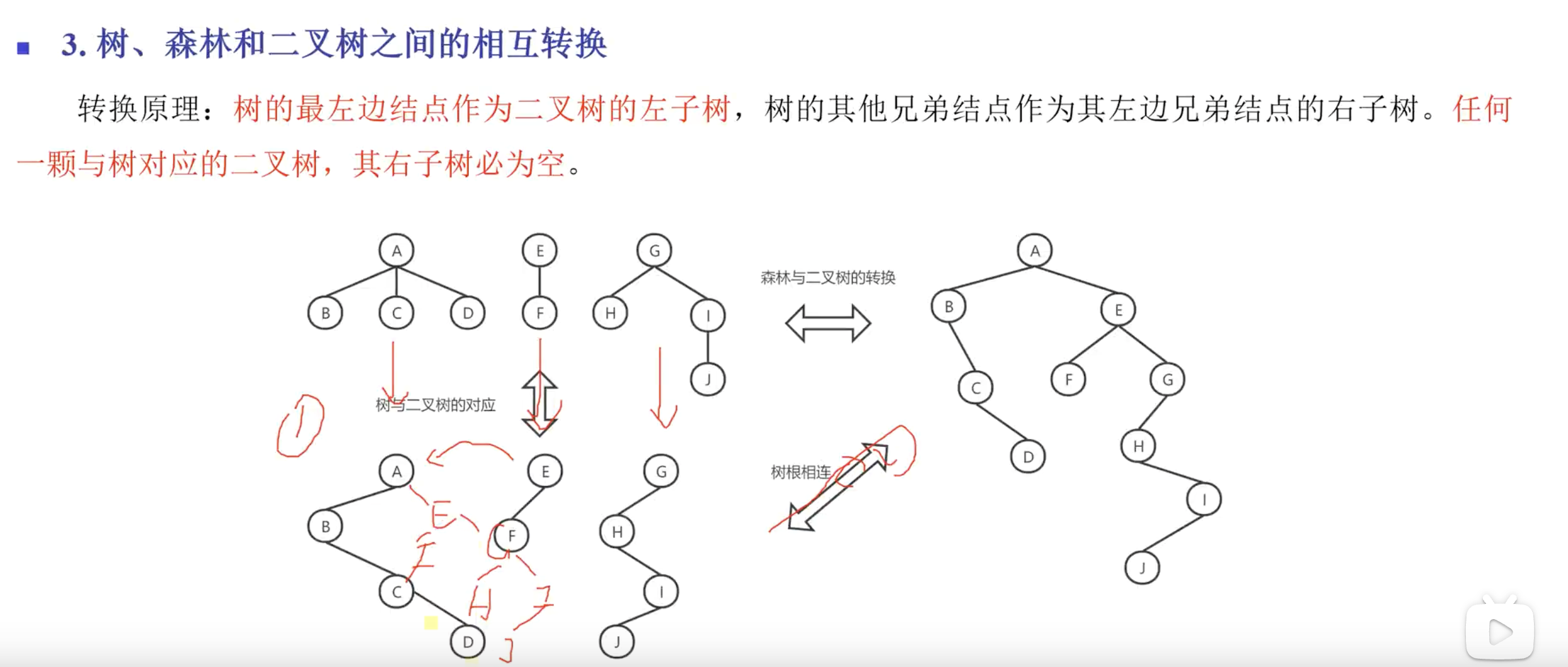
这里需要注意如何将树,森林和二叉树之间的转换
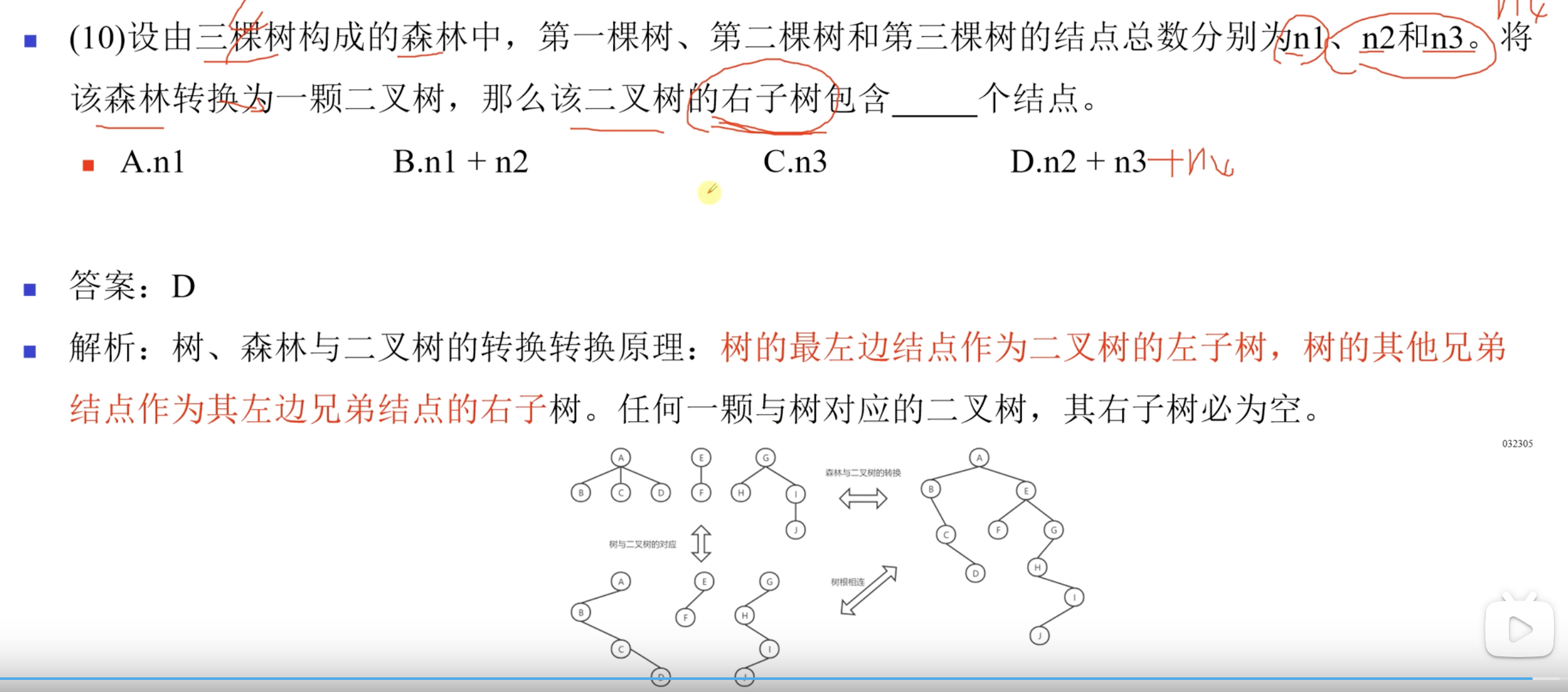

















![[SS]语义分割_膨胀卷积](http://pic.xiahunao.cn/[SS]语义分割_膨胀卷积)

)
