数学建模【聚类模型】

一、聚类模型简介

“物以类聚，人以群分”，所谓的聚类，就是将样本划分为由类似的对象组成的多个类的过程。聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测，也可以探究不同类之间的相关性和主要差异。

聚类和分类的区别：分类是已知类别的，聚类未知。

注：聚类模型一般有三种算法，K-means++法、系统层次法和DBSCAN法。

二、适用赛题

只有一对数据，要求将数据分为几类，类数不定。如有全国34个省的关于消费水平的几个指标，现要求将34个省分为几类分析。

三、模型流程

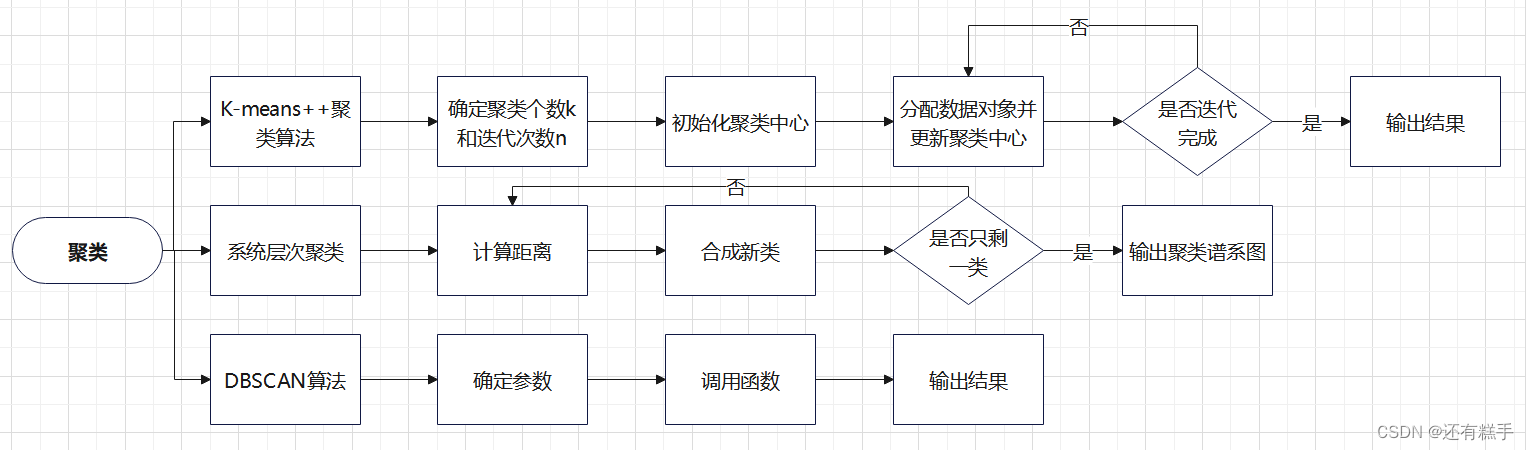
四、流程解析

1.K-means++聚类算法

K-means++算法是由K-means算法改进而来，对于K-means算法

优点

算法简单、快速
对处理大数据集，该算法是相对高效率的

缺点

要求用户必须事先给出要生成的簇的数目K
对初值敏感
对于孤立点数据敏感

而K-means++算法可解决后两个缺点。

①确定参数

聚类个数也就是簇的个数，也就是像分为多少个类。

迭代次数是指数据每经过一次迭代，都会有不同的数据进入不同的类，直到达到最大迭代次数，一般10次后，每次迭代后类中的数据就不会改变了。

②初始化聚类中心

这里就是优化的地方。K-means算法在初始化的时候，只是随机地选择K个数据对象作为初始的聚类中心。而K-means++算法选择初始聚类中心的基本原则是：初始的聚类中心之间的相互距离要尽可能的远。

具体流程如下

随机选取一个样本作为第一个聚类中心
计算每个样本与当前已有聚类中心的最短距离（即与最近一个聚类中心的距离），这个值越大，表示被选取作为聚类中心的概率较大。最后，用轮盘法（依据概率大小来进行抽选）选出下一个聚类中心
重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了

③分配和更新

分配数据对象是指计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中变成一个新类。

更新聚类中心是指重新计算出新类的中心，新的中心就是所有数据对象的重心。

下面是K-means算法的演示图

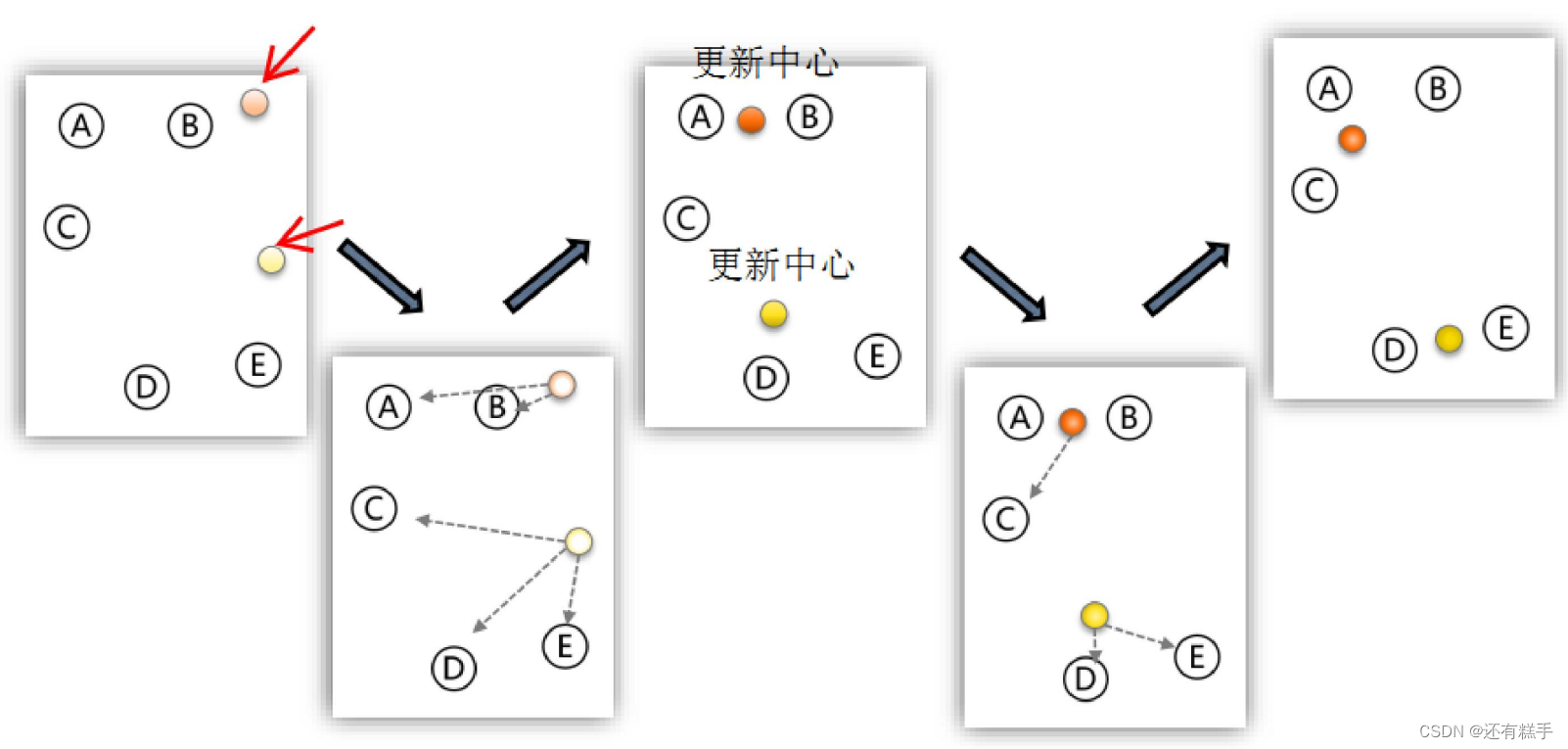
④输出结果

当完成迭代次数后，得到结果。

⑤补充

聚类的个数K值怎么定？

答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值,看分成几类的结果更好解释，更符合分析目的等。

数据的量纲不一致怎么办？

答：如果数据的量纲不一样，那么算距离时就没有意义。例如:如果X1单位是米，X2单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了。这就需要标准化。

这里还是推荐使用SPSS软件进行操作。

2.系统层次聚类

系统聚类的合并算法通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有数据点合成一类，并生成聚类谱系图。

①计算距离

这里根据问题看是求谁的距离，一般是样品之间距离，也有可能是求指标之间的距离。数据的一般格式如下图

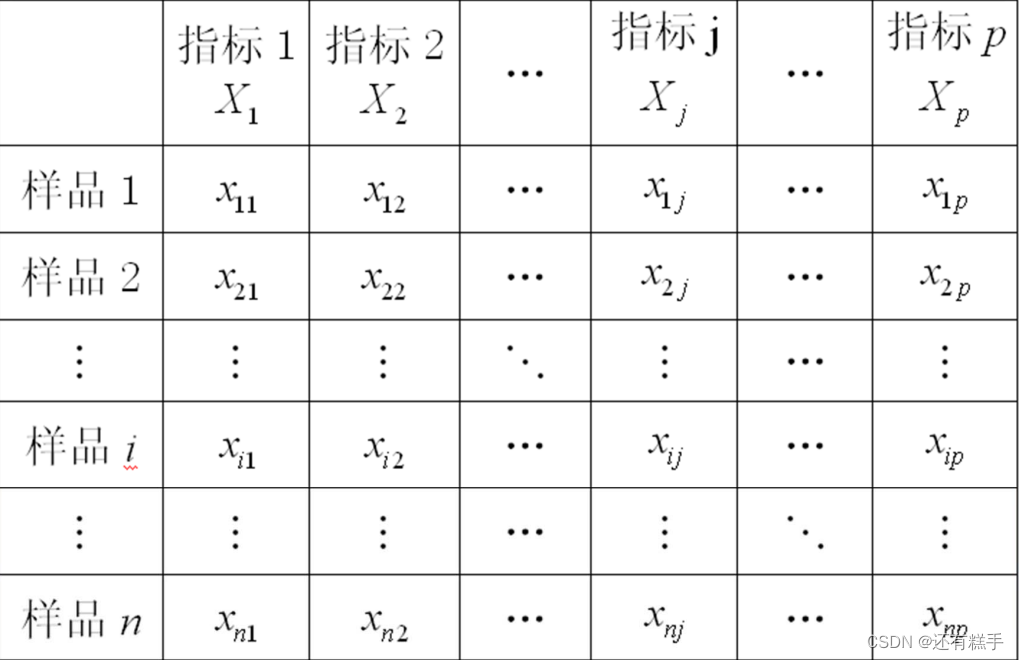
样品与样品之间的常用距离（样品i与样品j）

指标与指标之间的常用“距离”（指标i与指标j）

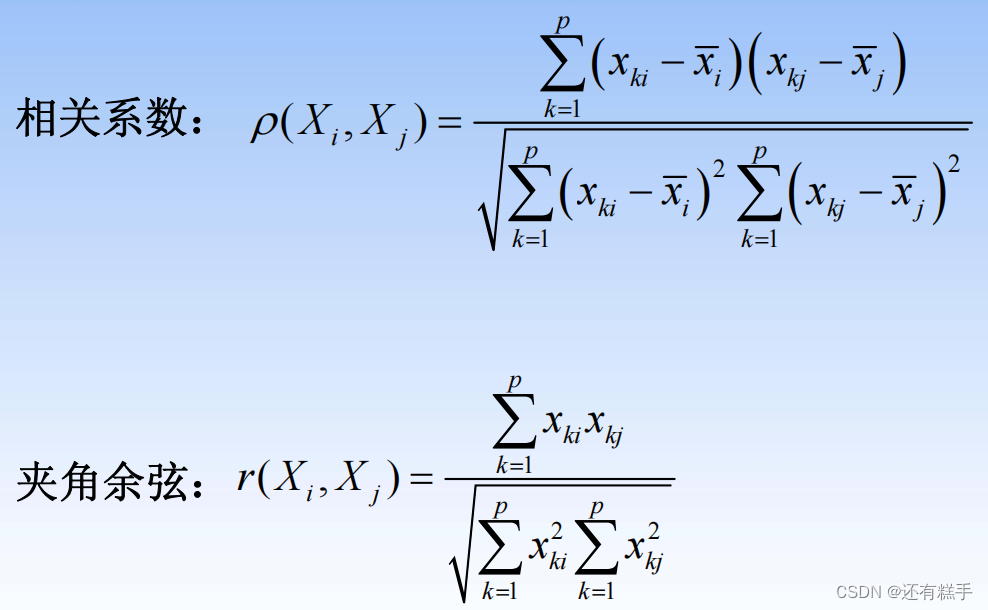
最开始的时候，将每个数据对象看作一类，计算两两之间的最小距离。后面是计算类与类之间的两两最小距离。

类与类之间的常用距离

由一个样品组成的类是最基本的类，如果每一类都由一个样品组成，那么样品间的距离就是类间距离
如果某一类包含不止一个样品，那么就要确定类间距离，类间距离是基于样品间距离定义的，大致有如下几种定义方式：

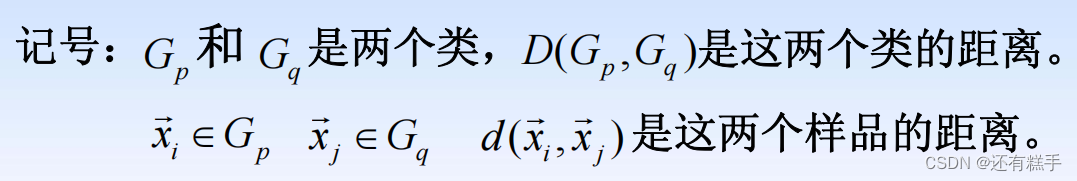
最短距离法（Nearest Neighbor）:

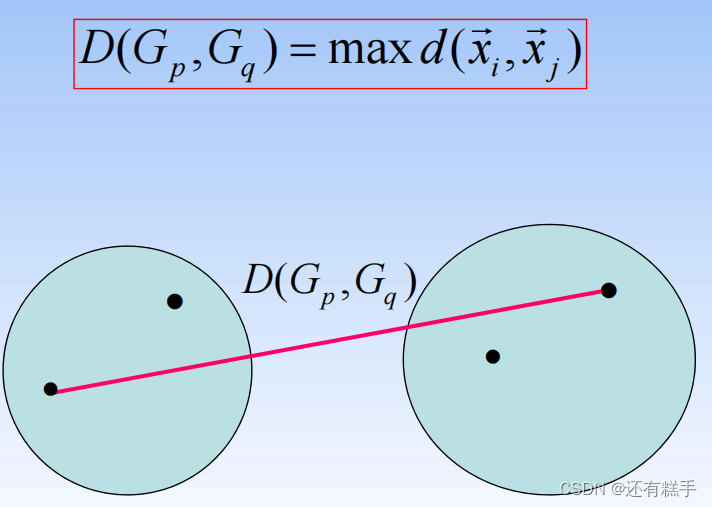
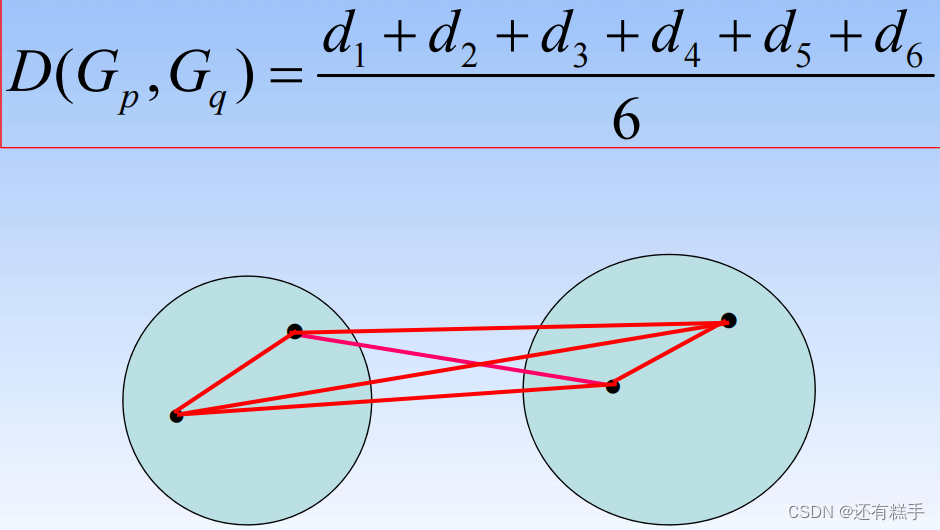
组间平均连接法（Between-group Linkage）：

组内平均连接法（Within-group Linkage）：

重心法（Centroid clustering）：

②合成新类

将距离最小的两个类合并成一个新类。

③迭代完成

重复计算距离、合成新类，直到最后只剩下一类也就是所有类合并成一类。

④聚类谱系图

下面就是一个聚类谱系图

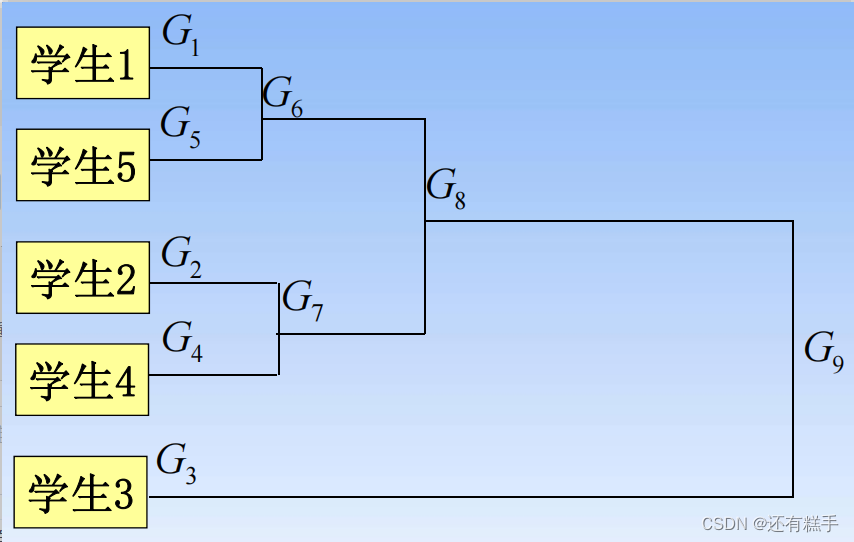
要分成几类只需要画竖线即可，有几个交点就有几个类，如下图

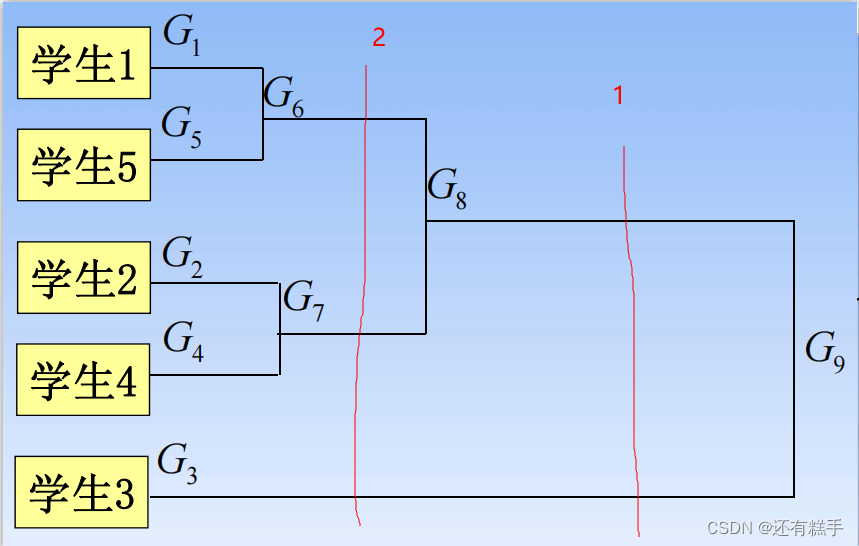
按照1分类就有两类，按照2分类就有三类。

⑤补充

那划成多少类才是最合适的？

肘部法则（Elbow Method）：通过图形大致的估计出最优的聚类数量。

首先介绍

然后得到如下图

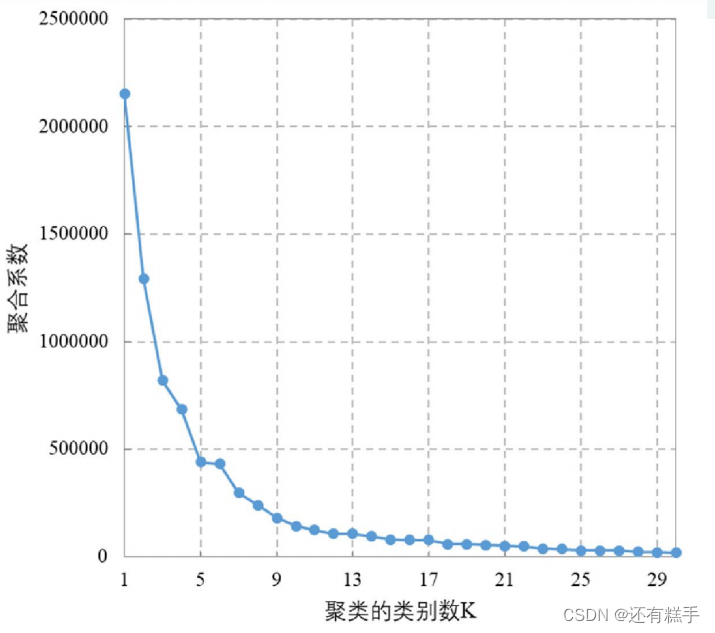
在下降趋势趋缓的时候选择，上图就选择K = 5。

这里还是推荐使用SPSS软件进行操作。

3.DBSCAN法

DBSCAN（Density-based spatial clustering of applicationswith noise）是Martin Ester，Hans- PeterKriegel等人于1996年提出的一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数，生成的簇的个数不定（和数据有关）。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据。

①确定参数

需要设置的参数

半径：Eps
点数：MinPts

DBSCAN算法将数据点分为三类

核心点：在半径Eps内含有不少于MinPts数目的点
边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
噪音点：既不是核心点也不是边界点的点

举个例子

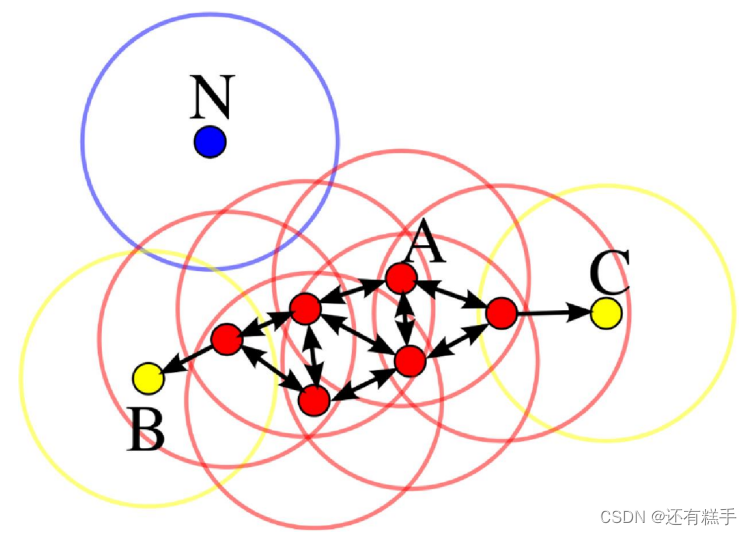
在这幅图里，MinPts = 4，点A和其他红色点是核心点，因为它们的Eps-邻域（图中红色圆圈）里包含最少4个点（包括自己），由于它们之间相互相可达，它们形成了一-个聚类。点B和点C不是核心点，但它们可由A经其他核心点可达，所以也和A属于同一个聚类。点N是局外点，它既不是核心点，又不由其他点可达。