电子技术——PN结电流关系方程
平衡状态下的PN结
平衡状态下的PN结界面总共有两种电流,一种为 扩散电流 另一种为 漂移电流 。两种电流形成的平衡区域称为 耗散区 。
在平衡状态扩散电流等于漂移电流,此时静电流为0,PN结外部没有电流:
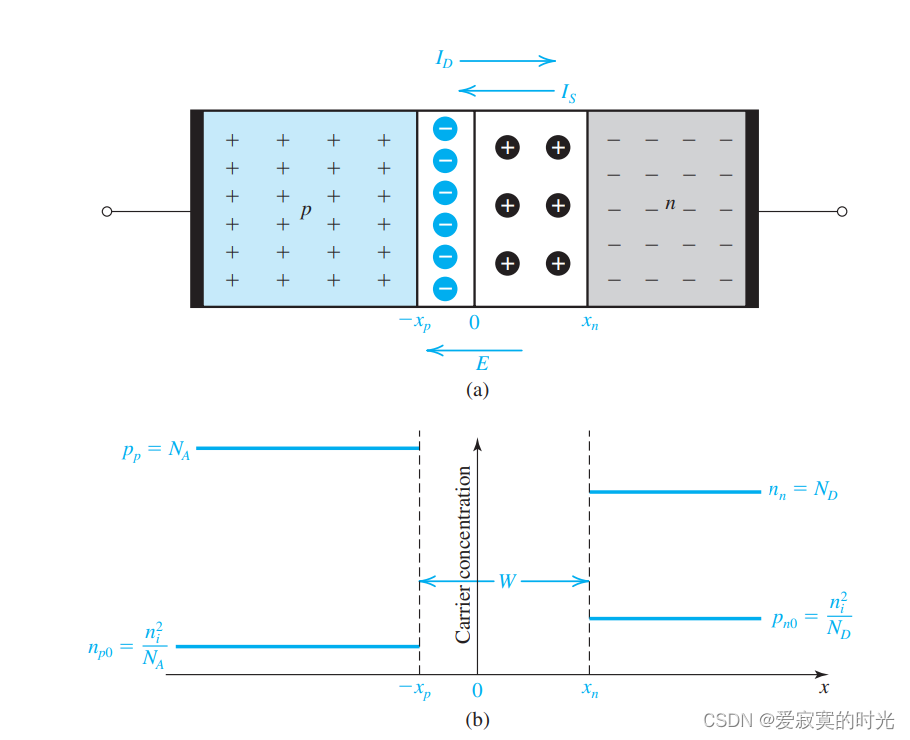
图中 I D I_D ID 为扩散电流, I S I_S IS 为漂移电流。 x n x_n xn 为耗散区 n n n 区域长度, − x p -x_p −xp 为耗散区 p p p 区域长度, W W W 为耗散区宽度。
n n n_n nn 为 n n n 区域主要载流子(电子)密度,等于掺杂浓度 N D N_D ND , p p p_p pp 为 p p p 区域主要载流子(空穴)密度,等于掺杂浓度 N A N_A NA 。
p n 0 p_{n0} pn0 为 n n n 区域次要载流子(空穴)密度,满足 玻尔兹曼条件下的密度关系方程 p n 0 = n i 2 N D p_{n0} = \frac{n^2_i}{N_D} pn0=NDni2 , n p 0 n_{p0} np0 为 p p p 区域次要载流子(电子)密度,满足 n p 0 = n i 2 N A n_{p0} = \frac{n^2_i}{N_A} np0=NAni2 。 n i n_i ni 为平衡次载流子密度(共价键断裂产生,与温度有关),平衡条件下有 p n = n n = n i p_n = n_n = n_i pn=nn=ni 。
由于扩散区中理想下不存在任何载流子,只有 贡献原子 和 接受原子 存在,PN结界面两边存在不同的净电荷,因此扩散区将形成 势垒电压 V 0 V_0 V0:

势垒电压阻止了PN结界面的浓度进一步扩散(电压与扩散方向相反),耗散区宽度处于恒定数值 W W W ,因此PN结处于平衡状态。
外加偏置电压状态下的PN结
当PN结处于外加偏置电压 V V V 下时,将会破坏PN结的平衡状态,此时PN结电流与外界电流一起处于 动态平衡 状态。
外界电流等于:
I = I D − I S I = I_D - I_S I=ID−IS
动态平衡下的PN结中, p p p 和 n n n 区域中的载流子密度不再是随位置变换的恒等函数,而是指数函数:

上图描述了PN处于 正偏置 下的浓度随位置的变化曲线,正偏置电压提供了更多的能量让载流子突破势垒电压,增大了扩散电流。
此时PN结对外界的电流表现为界面 − x p -x_p −xp 与 x n x_n xn 的密度梯度扩散电流,等价于 I = I D − I S I = I_D - I_S I=ID−IS ,正偏置下表现为:
扩散电流大于漂移电流 I D > I S I_D > I_S ID>IS ,此时会有额外的空穴进入 n n n 区域,通过外部电路流回 p p p 区域,因此界面 x n x_n xn 处的 p n p_n pn 浓度上升,同理 − x p -x_p −xp 界面的 n p n_p np 浓度也上升。
对于负偏置电压下的浓度随位置的变化曲线:
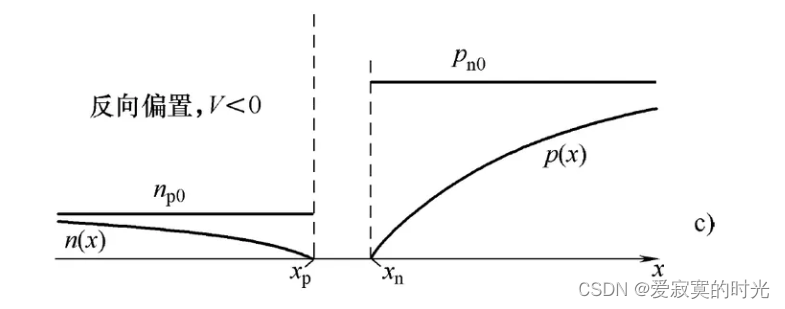
反向偏置电压增大了扩散的壁垒能量,扩散电流几乎为0,但漂移电流几乎保持不变(漂移现象由粒子热运动有关),此时 n n n 区域中的耗散区缺少空穴,空穴通过 n n n 区域进入耗散区,导致界面 x n x_n xn 处的 p n p_n pn 浓度下降,同理 − x p -x_p −xp 界面的 n p n_p np 浓度也下降,下降最低点为0(浓度不能为负数)。
通过半导体物理学,界面 x n x_n xn 的密度随外界偏置电压的变化关系为:
p n ( x n ) = p n 0 e V / V T p_n(x_n) = p_{n0}e^{V/V_T} pn(xn)=pn0eV/VT
当 V V V 为负无穷的时候(反向偏置电压无限大),此时 p n ( x n ) = 0 p_n(x_n) = 0 pn(xn)=0 ,但当 V V V 表现为正电压的时候, p n ( x n ) p_n(x_n) pn(xn) 随 V V V 指数上升(PN结单向导电性)。
同样当 x > x n x > x_n x>xn 密度随位置呈现指数变化,关系为:
p n ( x ) = p n 0 + p n 0 ( e V / V T − 1 ) e − ( x − x n ) / L p p_n(x) = p_{n0} + p_{n0}(e^{V/V_T} - 1) e^{-(x-x_n)/L_p} pn(x)=pn0+pn0(eV/VT−1)e−(x−xn)/Lp
当 x = x n x = x_n x=xn 的时候, p n ( x n ) = p n 0 e V / V T p_n(x_n) = p_{n0}e^{V/V_T} pn(xn)=pn0eV/VT 。
L p L_p Lp 称为 扩散长度 。
界面的梯度电流为:
J p ( x ) = − q D p d p n ( x ) d x J_p(x) = -q D_p \frac{dp_n(x)}{dx} Jp(x)=−qDpdxdpn(x)
带入得到:
J p ( x n ) = q ( D p L p ) p n 0 ( e V / V T − 1 ) J_p(x_n) = q (\frac{D_p}{L_p}) p_{n0} (e^{V/V_T} - 1) Jp(xn)=q(LpDp)pn0(eV/VT−1)
其中 D p D_p Dp 为空穴的扩散速率,与空穴的漂移速率满足 爱因斯坦关系 :
D n μ n = D p μ p = V T \frac{D_n}{\mu_n} = \frac{D_p}{\mu_p} = V_T μnDn=μpDp=VT
V T V_T VT 为热电压 μ p \mu_p μp 为空穴的漂移速率。
同理:
J n ( − x p ) = q ( D n L n ) n p 0 ( e V / V T − 1 ) J_n(-x_p) = q (\frac{D_n}{L_n}) n_{p0} (e^{V/V_T} - 1) Jn(−xp)=q(LnDn)np0(eV/VT−1)
总电流为:
I = A ( J p + J n ) = A q ( D p L p p n 0 + D n L n n p 0 ) ( e V / V T − 1 ) = A q n i 2 ( D p L p N D + D n L n N A ) ( e V / V T − 1 ) I = A(J_p + J_n) = Aq(\frac{D_p}{L_p} p_{n0} + \frac{D_n}{L_n} n_{p0}) (e^{V/V_T} - 1) = Aqn^2_i (\frac{D_p}{L_p N_D} + \frac{D_n}{L_n N_A}) (e^{V/V_T} - 1) I=A(Jp+Jn)=Aq(LpDppn0+LnDnnp0)(eV/VT−1)=Aqni2(LpNDDp+LnNADn)(eV/VT−1)
当 V V V 为负无穷的时候,我们知道 I I I 的大小等于 I S I_S IS ,因此:
I = I S ( e V / V T − 1 ) I = I_S (e^{V/V_T} - 1) I=IS(eV/VT−1)
I S = A q n i 2 ( D p L p N D + D n L n N A ) I_S = Aqn^2_i (\frac{D_p}{L_p N_D} + \frac{D_n}{L_n N_A}) IS=Aqni2(LpNDDp+LnNADn)
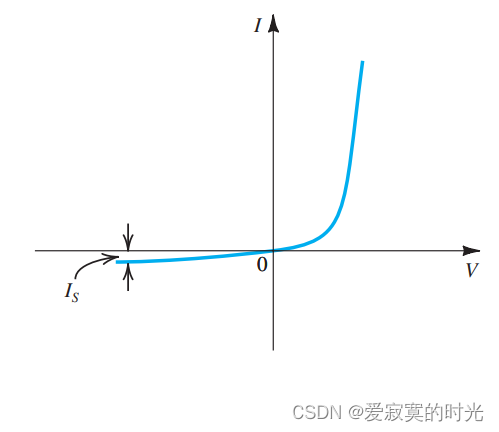
I S I_S IS 称为 饱和电流 ,因为与界面面积 A A A 有关,又称为 比例电流 。 I S I_S IS 又正比于 n i 2 n^2_i ni2 ,因此又和温度有关。表达式 I = I S ( e V / V T − 1 ) I = I_S (e^{V/V_T} - 1) I=IS(eV/VT−1) 的图像为:


挂载硬盘/数据盘详细操作和开机自动挂载的两种方式)


之同态滤波)



)




)




